【真香笔记இ௰இ】图论复习

文章开头第一句：回家旅游一时爽，集训复习火葬场
我说的是复习，真的是复习。（假装自己学过的样子。。
Day13-Day21 图论
图论分为三个方向：

1. 最短路径
2. 最小生成树
3. 树形dp、最近公共祖先LCA
4. 连通图和欧拉回路
5. 二分图匹配、拓扑排序
6. 网络流

1、最短路径

三个（准确的说来是四个算法）

1. Floyd算法：多源正权图，动态规划思想，时间复杂度n³
2. Dijkstra算法：单源正权图，贪心思想，时间复杂度n²
3. BF算法：单源可负权，动态规划+贪心，时间复杂度VE（点数边数）
4. SPFA算法，即队列优化后的BF算法

dijkstra和队列优化的SPFA必须掌握，学长的建议：

关于dijkstra的灵活应用中，差分约束系统第二题不会也找不到原题
分层图不理解

2、最小生成树

1. kuskall加边算法：贪心思想，类似dijkstra（离散课用的多的）
2. prim加点算法：动归+贪心，类似BF算法（离散课也讲过，用的少）

3、树形dp、 LCA

树形dp：什么鬼？
树的直径： 顾名思义，一棵树中两点间最远的距离就是这棵树的直径
怎么找树的直径： 两次BFS或DFS，第一次任取一点BFS/DFS找距离最远的点，第二次就用这个点再BFS/DFS找一次最远的点，最后这两点连接起来就是直径。已经画图推导成功，貌似推导没有什么实际意义，方便记忆求法而已
最近公共祖先LCA： 顾名思义，就是两个点的公共祖先中最近的那个。类似最小公倍数一样的东西。
怎么求LCA： 掌握树上倍增法、tarjan并查集优化的向上标记法即可。

4、连通图、欧拉回路

1. tarjan算法：求无向图的割点、割边，从而求得双连通分量个数
   求有向图的强连通分量个数、必经点和必经边
2. 圈套圈算法：求欧拉边图（可以得到欧拉回路）

5、二分图匹配、拓扑排序

二分图：就是对偶图
交替路：指一个匹配的路径
最大匹配：是所有匹配中边数最多的，但不一定所有点都在匹配中
完美匹配：是所有匹配中包含所有点的匹配
匈牙利算法：求二分图的最大匹配
最小顶点覆盖数：求一匹配能取最少的点覆盖所有边=求最大匹配的边数
最小路径（边）覆盖数：求一匹配能去最少的边覆盖所有点=n-最小点覆盖数=n-最大匹配数
二分图多重匹配：指在最大匹配的基础上，一个点不再只能与一条边相关联，而可以与L条边相关联
二分图的判定：不存在奇数长度的回路，BFS或DFS模板准备一下
拓扑排序：拓扑排序不是排序，是一种序列，适用于有向无环图，这个序列包含所有的点 ，并且A如果能到达B，那么A就排在B的前面
有向图判环：解决多个关系是否有矛盾的问题

6、网络流

网络流问题就是，求一张图从起点到终点的流量的问题。
流函数f：表示实际流量，流函数有三个性质：容量限制、斜对称性（f(A,B)=-f(B,A)）和流量守恒（源点出的=汇点进的）。
最大流：我终于弄明白了，不是每条边想最大就最大，主要是流量守恒性妹整（zen）明白，按照下图给的网络的容量，最大流只能是：（第一个f错了应该是1，2，4，7）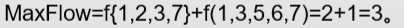

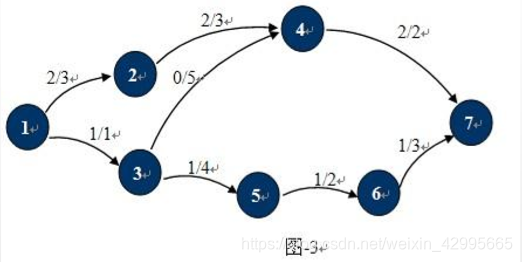
残留网络：=容量网络-流量网络，例如，按照上图的容量来看，这次网络流的残留网络是红色线的权值：

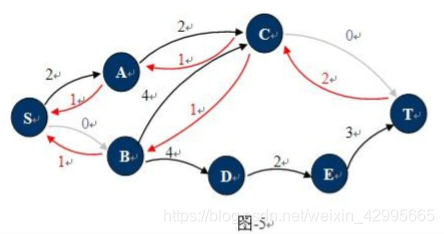
增广路：就是一条路径，他的每条边在残留网络上的权值都大于零。
EK算法：求最大流
dinic算法：求最大流，性能更好。
网络流求解二分图的最大匹配：将起点与第一个集合每个点建立一个容量为1的关系，终点与第二个集合每个点建立一个容量为1的关系，所求的最大流就是此二分图的最大匹配。
网络流求二分图的多重匹配：方法与上面一样，只是建立容量不为1，而是此点最大关联边数L
割集：你懂的吧，割边的集合
最小割：割集中边最少的呗
最大流最小割定理：最大流=最小割中的所有边的容量之和