先上神图,哈哈哈哈。

题A:美丽的2
题目:
小蓝特别喜欢 2,今年是公元 2020 年,他特别高兴。
他很好奇,在公元 1 年到公元 2020 年(包含)中,有多少个年份的数位中包含数字 2?
分析:
暴力法
代码:
public static void main(String[] args) {
int ans = 0;
for (int i = 0; i < 2021; i++) {
if(hava2(i)) ans++;
}
System.out.println(ans);
}
public static boolean hava2(int num) {
while(num > 0) {
if(num % 10 == 2) return true;
num /= 10;
}
return false;
}
答案:
563
题B:扩散
题目:
小蓝在一张无限大的特殊画布上作画。
这张画布可以看成一个方格图,每个格子可以用一个二维的整数坐标表示。
小蓝在画布上首先点了一下几个点:(0, 0), (2020, 11), (11, 14), (2000, 2000)。
只有这几个格子上有黑色,其它位置都是白色的。
每过一分钟,黑色就会扩散一点。具体的,如果一个格子里面是黑色,它
就会扩散到上、下、左、右四个相邻的格子中,使得这四个格子也变成黑色
(如果原来就是黑色,则还是黑色)。
请问,经过 2020 分钟后,画布上有多少个格子是黑色的。
分析:
从(x,y)位置出发,经过2020时间,黑点构成一个菱形,坐标为
上(x,y+2020)
下(x,y-2020)
左(x-2020,y)
右(x+2020,y)
为了使用数组处理方便,整体上移2020格,且向右移动2020
从(x,y)位置出发,经过t时间,黑点构成一个菱形,坐标为
上(x,y+4040)
下(x,y-4040)
左(x-4040,y)
右(x+4040,y)
依次将四个菱形填充,然后遍历整个数组,统计数量即可。

代码:
public static void main(String[] args) {
coloring(0, 0);
coloring(11, 14);
coloring(2020, 11);
coloring(2000, 2000);
int sum = 0;
for (int i = 0; i < canvas.length; i++) {
for (int j = 0; j < canvas[0].length; j++) {
if(canvas[i][j]) sum++;
}
}
System.out.println(sum);
}
static boolean[][] canvas = new boolean[7000][7000];
// 根据给定坐标点,绘制2020分钟之后的情况
public static void coloring(int x,int y) {
int k = 2020;
x += 2020;
y += 2020;
for (int i = 0; i <= 2020; i++) {
for (int j = k; j >= 0; j--) {
canvas[x-j][y+i] = true;
canvas[x+j][y+i] = true;
canvas[x-j][y-i] = true;
canvas[x+j][y-i] = true;
}
k--;
}
}
答案:
20312088
题C:阶乘约数
题目:
定义阶乘 n! = 1 × 2 × 3 × · · · × n。
请问 100! (100 的阶乘)有多少个约数。
分析:
是算数基本定理的一个应用。
若要求100!的质数乘积形式,没有必要计算100!
只需要求出2~100每个数的质数乘积形式,再将幂累计起来就行。
显然,100!不存在大于100的质因数
先计算小于100的所有素数按从小到大存入数组prim
将次方存入对应的power数组的位置.
100可以表示为:
2 3 5 7 ... prim[]
2 0 2 0 ...power[]
计算完100!的质数乘积表示,使用算数基本定理的应用一,即得所求。
代码:
public static void main(String[] args) {
// 求小于100的所有素数
int[] prim = ola(100);
int[] power = new int[prim.length];
// 将100!用算数基本定理表示
for (int i = 2; i <= 100; i++) {
int temp = i;
// 将1~100每个数用算数基本定理表示,再power数组中记录对应的次数
for (int j = 0; j < prim.length; j++) {
while(temp % prim[j] == 0) {
power[j]++;
temp /= prim[j];
}
if(temp < 2) break;
}
}
// 计算最终答案
long ans = 1;
for (int i = 0; i < power.length; i++) {
ans *= (1+power[i]);
}
System.out.println(ans);
}
// 使用欧拉筛寻找小于n的所有素数
public static int[] ola(int n){
int cnt = 0; // 质数的个数
int[] primes = new int[n+1]; // 用于存储质数
int[] st = new int[n+1];
for(int i = 2; i <= n; i++) {
if(st[i] == 0) primes[cnt++] = i;
for(int j = 0; primes[j] <= n / i; j++) {
st[primes[j]*i] = 1;
if(i % primes[j] == 0) break;
}
}
int[] ans = new int[cnt];
for (int i = 0; i < ans.length; i++) {
ans[i] = primes[i];
}
return ans;
}
答案:
39001250856960000
算数基本定理
任何一个大于1的自然数N,且N不是质数,则N一定可以写成有限个质数的乘积的形式。

pi是不同的质数,ai是对应的次方数。
例如:

应用一:
可以求N的正因数的个数,
可以通过p1、p2...pn取不同的次数来组合出来所有的因数。
比如:
p1 有 (a1+1)种取法
p2 有 (a2+1)种取法
...
pn 有 (an+1)种取法
所以有:N的正因数的个数 = (a1+1) * (a2+1) * ... * (an+1)
应用二:
求N的全体正因数的和
其实还是按上面的取法,把所有的取法相加,再合并同类项可得:

题D:本质上升序列
题目:
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串:
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
分析:
不讲武德的直接暴力枚举
用枚举生成所有的字符序列,将它们放到一个set中,再使用适当的剪枝。
数据规模不是很大,跑个半个小时差不多能跑出来。
讲武德的一般都上动态规划
设dp[i][1-26]:表示的是前i个元素,以26个字母结尾的字符串的个数
比如:
dp[i][0]:表示前i个元素中,以a结尾的字符串的个数。
dp[i][1]:表示前i个元素中,以b结尾的字符串的个数。
...
如果第i个元素是q,
初始:dp[i][16] = 1,表示单个q这个字符串
dp[i-1][1~15]表示的是前 i-1 个元素,以 a~p结尾的字符串
显然这些字符串都能在结尾补上一个 q 构成以 q 结尾的字符串。
意思就是dp[i-1]中以小于第i个字符结尾的字符串的数量的求和再加1 构成了dp[i]这一行唯一改变的值,dp[i]的其他位置的值不变。
既然这样。那完全可以压缩成一行。来减少空间的开销。

代码:
String str =
int[] dp = new int[26];
for (int i = 0; i < 200; i++) {
int now = str.charAt(i) - 'a';
dp[now] = 1;
for (int j = 0; j < now; j++)
dp[now] += dp[j];
}
long res = 0;
for (int i = 0; i < 26; i++)
res += dp[i];
System.out.println(res);
答案:
3616159
题E:玩具蛇
题目:
小蓝有一条玩具蛇,一共有 16 节,上面标着数字 1 至 16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4 的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母 A 到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:

请帮小蓝计算一下,总共有多少种不同的方案。如果两个方案中,存在玩具蛇的某一节放在了盒子的不同格子里,则认为是不同的方案
分析:
还是典型的回溯,从(0,0)位置出发的搜索树如下图所示:

也没必要进行16遍dfs,
由于正方形的对称性,图中的点分为三类,只需要搜索3次,再乘上相应的倍数即可。

代码:
public static void main(String[] args) {
int realAns = 0;
dfs(0, 0, 1);
realAns = ans * 4;
ans = 0;
dfs(0, 1, 1);
realAns += ans * 8;
ans = 0;
dfs(1, 1, 1);
realAns += ans * 4;
System.out.println(realAns);
}
static int[][] box = new int[4][4];
static int ans = 0;
public static void dfs(int x, int y, int nextNum) {
if(nextNum == 16) {
ans++;
return;
}
box[x][y] = nextNum;
// 向上下左右四个方向试探
if(x>0 && box[x-1][y]==0) dfs(x-1, y, nextNum+1);
if(x<3 && box[x+1][y]==0) dfs(x+1, y, nextNum+1);
if(y>0 && box[x][y-1]==0) dfs(x, y-1, nextNum+1);
if(y<3 && box[x][y+1]==0) dfs(x, y+1, nextNum+1);
box[x][y] = 0;
}
答案:
552
题F:蓝肽子序列
题目:
L 星球上的生物由蛋蓝质组成,每一种蛋蓝质由一类称为蓝肽的物资首尾连接成一条长链后折叠而成。
生物学家小乔正在研究 L 星球上的蛋蓝质。她拿到两个蛋蓝质的蓝肽序列,想通过这两条蓝肽序列的共同特点来分析两种蛋蓝质的相似性。
具体的,一个蓝肽可以使用 1 至 5 个英文字母表示,其中第一个字母大写,后面的字母小写。一个蛋蓝质的蓝肽序列可以用蓝肽的表示顺序拼接而成。
在一条蓝肽序列中,如果选取其中的一些位置,把这些位置的蓝肽取出,并按照它们在原序列中的位置摆放,则称为这条蓝肽的一个子序列。蓝肽的子序列不一定在原序列中是连续的,中间可能间隔着一些未被取出的蓝肽。
如果第一条蓝肽序列可以取出一个子序列与第二条蓝肽序列中取出的某个子序列相等,则称为一个公共蓝肽子序列。
给定两条蓝肽序列,找出他们最长的那个公共蓝肽子序列的长度。
输入输出:
输入两行,每行包含一个字符串,表示一个蓝肽序列。字符串中间没有空格等分隔字符。
输出一个整数,表示最长的那个公共蓝肽子序列的长度。
样例输入:
LanQiaoBei
LanTaiXiaoQiao
输出:
2
说明:
最长的公共蓝肽子序列为 LanQiao,共两个蓝肽。
规模:
对于 20% 的评测用例,两个字符串的长度均不超过 20。
对于 50% 的评测用例,两个字符串的长度均不超过 100。
对于所有评测用例,两个字符串的长度均不超过 1000。
分析:
设输入的两个字符串分别为a和b
设dp[i][j]表示a的前i个和b的前j个的最长公共子序列的长度。
显然有
边界条件:
dp[0][j]和dp[i][0]都是0
递推关系:
如果 a[i]==b[j],dp[i][j] = dp[i-1][j-1] + 1
如果 a[i]!=b[j],dp[i][j] = max(dp[i-1][j],dp[i][j-1])
代码:
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s1 = sc.nextLine();
String s2 = sc.nextLine();
int[] a = subStrings(s1);
int[] b = subStrings(s2);
int ans = maxSubsequence(a, b);
System.out.println(ans);
}
public static int maxSubsequence(int[] a,int[] b) {
int[][] dp = new int[a.length+1][b.length+1];
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[0].length; j++) {
if(a[i-1] == b[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = dp[i-1][j] > dp[i][j-1] ? dp[i-1][j] : dp[i][j-1];
}
}
return dp[a.length][b.length];
}
public static int[] subStrings(String s) {
// 切割
int len = 0;
for (int i = 0; i < s.length(); i++) {
if(s.charAt(i)<97) len++;
}
s += "A";
int[] a = new int[len];
int pro = 0,j = 0;
for (int i = 1; i < s.length(); i++) {
if(s.charAt(i)<97) {
a[j++] = s.substring(pro,i).hashCode();
pro = i;
}
}
return a;
}
题G:皮亚诺曲线
题目:
皮亚诺曲线是一条平面内的曲线。
下图给出了皮亚诺曲线的 1 阶情形,它是从左下角出发,经过一个 3 × 3 的方格中的每一个格子,最终到达右上角的一条曲线。
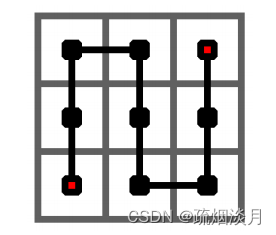
下图给出了皮亚诺曲线的 2 阶情形,它是经过一个 3^2 × 3^2 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。

下图给出了皮亚诺曲线的 3 阶情形,它是经过一个 3^3 × 3^3 的方格中的每一个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发,最终到达右上角。
我们将这些格子放到坐标系中,对于 k 阶皮亚诺曲线,左下角的坐标是(0, 0),右上角坐标是 (3^k - 1, 3^k - 1),右下角坐标是 (3^k 1, 0),左上角坐标是(0, 3^k - 1)。
给定 k 阶皮亚诺曲线上的两个点的坐标,请问这两个点之间,如果沿着皮亚诺曲线走,距离是到少?
输入输出:
输入的第一行包含一个正整数 k,皮亚诺曲线的阶数。
第二行包含两个整数 x1, y1,表示第一个点的坐标。
第三行包含两个整数 x2, y2,表示第二个点的坐标。
输出一个整数,表示给定的两个点之间的距离。
样例输入1:
1
0 0
2 2
样例输出1:
8
样例输入2:
2
0 2
0 3
样例输出2:
13
规模:
对于 30% 的评测用例,0 ≤ k ≤ 10。
对于 50% 的评测用例,0 ≤ k ≤ 20。
对于所有评测用例,0 ≤ k ≤ 100, 0 ≤ x1, y1, x2, y2 < 3^k, x1, y1, x2, y2 ≤ 10^18。
数据保证答案不超过 10^18。
分析:
可以将问题转化为,计算从左下角沿着皮亚诺曲线走到两点的距离差。
这样问题就转化为,计算从左下角沿着皮亚诺曲线走到某点的距离。
假设当前皮亚诺曲线的阶数为 K,那么走过一个完整的 k-1 阶曲线的距离是确定的。
我们只需要确定当前点所在的 k-1 阶在九宫格中的位置,就能知道从起点到当前点走了多少个 k-1 阶曲线,
问题就转化为求当前点在k-1阶曲线中与入口的距离。
比较头疼的是,子曲线并不是每次都是从左下角走到右上角,但是可以通过对曲线进行反转得到,
设 从左下角走到右上角 的皮亚诺曲线为标准曲线,
设 1 表示经过左右翻转可得到标准曲线,
设 2 表示经过上下翻转可得到标准曲线,
设 3 表示经过左右翻转+上下反转可得到标准曲线,
则转化模板为:

当然,实际求的时候,我们不必将曲线翻转,直接将点的坐标进行反翻转,然后放到标准曲线中求距离即可。
可以递归向下求,
代码1 :long版本
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int k = sc.nextInt();
long x1 = sc.nextLong();
long y1 = sc.nextLong();
long x2 = sc.nextLong();
long y2 = sc.nextLong();
System.out.println(Math.abs(distance(x1, y1, k)-distance(x2, y2, k)));
}
static int[][] change = {{0,1,0},{2,3,2},{0,1,0}};
static int[][] basicMap = {{1,2,3},{6,5,4},{7,8,9}};
public static long distance(long x,long y,int k) {
if(k == 1) return basicMap[(int)x][(int)y];
// 计算所处的 k-1 阶曲线的位置
long xi = x / quickPower(3, k-1);
long yi = y / quickPower(3, k-1);
// 完整的 k-1 阶曲线的长度
long distance1 = (basicMap[(int)xi][(int)yi]-1) * quickPower(3, 2*k-2);
// 坐标转化
// 1、降阶
x = x % quickPower(3, k-1);
y = y % quickPower(3, k-1);
// 2、翻转
if(change[(int)xi][(int)yi] == 1) x = quickPower(3, k-1) - 1 - x;
if(change[(int)xi][(int)yi] == 2) y = quickPower(3, k-1) - 1 - y;
if(change[(int)xi][(int)yi] == 3) {
x = quickPower(3, k-1) - 1 - x;
y = quickPower(3, k-1) - 1 - y;
}
long distance2 = distance(x, y, k-1);
return distance1+distance2;
}
public static long quickPower(long a, long n) {
long ans = 1;
while(n > 0) {
if(n % 2 == 1) ans *= a;
a *= a;
n /= 2;
}
return ans;
}
上面这个没法全部通过示例,因为3^100次方肯定越了long的界了。下面改成BigInteger。
代码2 :BigInteger
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int k = sc.nextInt();
sc.nextLine();
String[] a = sc.nextLine().split(" ");
String[] b = sc.nextLine().split(" ");
BigInteger x1 = new BigInteger(a[0]);
BigInteger y1 = new BigInteger(a[1]);
BigInteger x2 = new BigInteger(b[0]);
BigInteger y2 = new BigInteger(b[1]);
System.out.println(distance(x1, y1, k).subtract(distance(x2, y2, k)).abs());
}
static int[][] change = {{0,1,0},{2,3,2},{0,1,0}};
static String[][] basicMap = {{"1","2","3"},{"6","5","4"},{"7","8","9"}};
static BigInteger three = new BigInteger("3");
static BigInteger one = new BigInteger("1");
public static BigInteger distance(BigInteger x,BigInteger y,int k) {
if(k == 1) return new BigInteger(basicMap[Integer.parseInt(x.toString())][Integer.parseInt(y.toString())]);
BigInteger threePower = three.pow(k-1);
// 计算所处的 k-1 阶曲线的位置
int xi = Integer.parseInt(x.divide(threePower).toString());
int yi = Integer.parseInt(y.divide(threePower).toString());
// 完整的 k-1 阶曲线的长度
BigInteger distance1 = (new BigInteger(basicMap[xi][yi])).subtract(one).multiply(threePower.pow(2));
// 坐标转化
// 1、降阶
x = x.mod(threePower);
y = y.mod(threePower);
// 2、翻转
if(change[xi][yi] == 1) x = threePower.subtract(one).subtract(x);
if(change[xi][yi] == 2) y = threePower.subtract(one).subtract(y);
if(change[xi][yi] == 3) {
x = threePower.subtract(one).subtract(x);
y = threePower.subtract(one).subtract(y);
}
BigInteger distance2 = distance(x, y, k-1);
return distance1.add(distance2);
}
题H:画廊
题目:
小蓝办了一个画展,在一个画廊左右两边陈列了他自己的作品。为了使画展更有意思,小蓝没有等距陈列自己的作品,而是按照更有艺术感的方式陈列。
在画廊的左边陈列了 L 幅作品,在画廊的右边陈列了 R 幅作品,左边的作品距离画廊的起点依次为 u1, u2, · · · , uL,右边的作品距离画廊起点依次为 v1, v2, · · · , vR。
每周,小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的,但是要带着沉重的工具。
从一幅作品到另一幅作品之间的距离为直线段的长度。
小蓝从画廊的起点的正中央(左右两边的中点)出发,整理好每一幅画,最终到达画廊的终点的正中央。已知画廊的宽为 w。
请问小蓝最少带着工具走多长的距离?
输入输出:
输入的第一行包含四个整数 L, R, d, w,表示画廊左边和右边的作品数量,以及画廊的长度和宽度。
第二行包含 L 个正整数 u1, u2, · · · , uL,表示画廊左边的作品的位置。
第三行包含 R 个正整数 v1, v2, · · · , vR,表示画廊右边的作品的位置。
输出一个实数,四舍五入保留两位小数,表示小蓝最少带着工具走的距离。
样例输入
3 3 10 2
1 3 8
2 4 6
样例输出
14.71
样例说明
小蓝从起点开始,首先到达左边第一幅作品(走动距离 √2),然后到达左边第二幅作品(走动距离 2),然后到达右边第一幅作品(走动距离 √5),然后到达右边第二幅和第三幅作品(走动距离 2 和 2),然后到达左边第三幅作品(走动距离 2 √2),最后到达画廊终点(走动距离√5)。
总共距离为 √2 + 2 + √5 + 2 + 2 + 2 √2 + √5 ≈ 14.71。
规模:
对于 40% 的评测用例,1 ≤ L, R ≤ 10, 1 ≤ d ≤ 100, 1 ≤ w ≤ 100。
对于 70% 的评测用例,1 ≤ L, R ≤ 100, 1 ≤ d ≤ 1000, 1 ≤ w ≤ 1000。
对于所有评测用例,1 ≤ L, R ≤ 500, 1 ≤ d ≤ 100000, 1 ≤ w ≤ 100000, 0 ≤ u1 < u2 < · · · < uL ≤ d, 0 ≤ v1 < v2 < · · · < vR ≤ d。
分析:
最初使用的贪心算法,但是只能过部分用例,分析原因可能是当下一步要走的两个点距离相同,应该如何选择的问题。
dp[i][j]表示经过左侧前i个和右侧前j个的最短距离,显然还要区分结束地点是左侧还是右侧,再加上一个维度。
dp[i][j][0]:表示经过左侧前i个和右侧前j个并且最终停到左侧的最短距离,
dp[i][j][1]:表示经过左侧前i个和右侧前j个并且最终停到右侧的最短距离,
有递推公式:
dp[i][j][0] = min(dp[i-1][j][0]+(直行距离), dp[i-1][j][1]+(转弯距离))
dp[i][j][1] = min(dp[i][j-1][0]+(转弯距离), dp[i][j-1][1]+(直行距离))
对于每个(i,j)而已,只用到了[i-1][j]和[i][j-1]这两个点,所以可以将dp压缩成二维表。
对于每个i有
dp[j][0] = min(dp[j][0]+(直行距离),dp[j][1]+(转弯距离)) // 显然要先更新 dp[i][0]
dp[j][1] = min(dp[j-1][0]+(转弯距离), dp[j-1][1]+(直行距离))
代码:
static int INF = 0x3f3f3f3f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int l = sc.nextInt();
int r = sc.nextInt();
double d = sc.nextInt();// 长度
double w = sc.nextInt();// 宽度
double wr = w / 2;
int[] ls = new int[l + 1];
int[] rs = new int[r + 1];
for (int i = 1; i <= l; i++) {
ls[i] = sc.nextInt();
}
for (int i = 1; i <= r; i++) {
rs[i] = sc.nextInt();
}
double[][] dp = new double[r+1][2];
double a = f(wr, ls[1]);
double b = f(wr, rs[1]);
for (int i = 1; i <= r; i++) { // i == 0
dp[i][1] = b + rs[i] - rs[1];
dp[i][0] = INF;
}
for (int i = 1; i <= l; i++) {
for (int j = 0; j <= r; j++) {
if(j==0) {
dp[0][0] = a + ls[i] - ls[1];
dp[0][1] = INF;
continue;
}
dp[j][0] = Math.min(dp[j][0] + ls[i] - ls[i - 1], dp[j][1] + f(w, abs(ls[i] - rs[j])));
dp[j][1] = Math.min(dp[j-1][0] + f(w, abs(ls[i] - rs[j])), dp[j-1][1] + rs[j] - rs[j-1]);
}
}
System.out.printf("%.2f", Math.min(dp[r][0] + f(wr, d - ls[l]), dp[r][1] + f(wr, d - rs[r])));
}
static double f(double a, double b) {
return sqrt(a * a + b * b);
}
题I:补给
题目:
小蓝是一个直升飞机驾驶员,他负责给山区的 n 个村庄运送物资。每个月,他都要到每个村庄至少一次,可以多于一次,将村庄需要的物资运送过去。每个村庄都正好有一个直升机场,每两个村庄之间的路程都正好是村庄之间的直线距离。
由于直升机的油箱大小有限,小蓝单次飞行的距离不能超过 D。每个直升机场都有加油站,可以给直升机加满油。
每个月,小蓝都是从总部出发,给各个村庄运送完物资后回到总部。如果方便,小蓝中途也可以经过总部来加油。
总部位于编号为 1 的村庄。
请问,要完成一个月的任务,小蓝至少要飞行多长距离?
输入输出:
输入的第一行包含两个整数 n, D,分别表示村庄的数量和单次飞行的距离。
接下来 n 行描述村庄的位置,其中第 i 行两个整数 xi, yi,表示编号为 i 的村庄的坐标。
村庄 i 和村庄 j 之间的距离为 √(xi - xj)^2 + (yi - yj)^2。
输出一行,包含一个实数,四舍五入保留正好 2 位小数,表示答案。
样例输入
4 10
1 1
5 5
1 5
5 1
样例输出
16.00
样例说明
四个村庄形成一个正方形的形状。
样例输入
4 6
1 1
4 5
8 5
11 1
样例输出
28.00
样例说明
补给顺序为 1 → 2 → 3 → 4 → 3 → 2 → 1。
规模
对于所有评测用例,1 ≤ n ≤ 20, 1 ≤ xi, yi ≤ 104, 1 ≤ D ≤ 105。
分析:
这道题是旅行商问题的一个变形。唯一的区别就是旅行商不能走重复的城市,但是补给可以重复经过某个村庄。
还是使用旅行商问题的基本框架,状压dp。
g[i][j]:从i村庄到j村庄的最短距离。
dp[i][j]:从原点出发经过(i集合)中的所有元素,到达j村庄,的最短距离。
用数字i表示一个集合
i的取值范围是[1,2^n],如果i的二进制表示的第j位是1,表示这个集合包含j村庄。
例如:
i = 5 = 101B = {1,3}
i = 7 = 111B = {1,2,3}
i = 14 = 1110B = {2,3,4}
...
为了方便数组表示,将村庄的代号从0表示,集合i也从0表示,等于说大家在原有基础上都进行了减一操作。
旅行商问题的常见操作:
村庄j的二进制表示:1<<j
对于一个集合i,判断是否包含第j个村庄:((i>>j) & 1) == 1
从集合i中剔除第j个村庄:i - 1<<j
求g[i][j]可以用floyd算法,求任意两点的最短距离。
对于任意不是j的村庄更新dp[i][j]
dp[i][j] = min(dp[i][j], dp[i - (1 << j)][k] + g[k][j])
另:
如果dp使用double类型的话,2^20 * 20 * 8 / (2 ^ 20) = 160MB,不知道内存会不会超。
啊啊啊,内存没超,最后一个用例超时。。。
最后将dp和g数组都转化为了int,既防止了内存超,也加快了计算。
代码:
static int INF = Integer.MAX_VALUE / 2;
static int[][] g;
static int[][] dp;
static int[][] p;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int d = sc.nextInt();
p = new int[n][2];
for (int i = 0; i < n; i ++) {
p[i][0] = sc.nextInt();
p[i][1] = sc.nextInt();
}
// 初始化 g 数组
g = new int[n][n];
for (int i = 0; i < n; i ++) {
for (int j = i + 1; j < n; j ++) {
g[i][j] = g[j][i] = (int)(get_distance(i, j)*10000);
if(g[i][j] > d*10000) g[i][j] = g[j][i] = INF;
}
}
// 使用 Floyd 算法完善 g 数组
for (int k = 0; k < n; k ++)
for (int i = 0; i < n; i ++)
for (int j = 0; j < n; j ++)
g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);
// 初始化 dp 数组
dp = new int[1<<n][n];
for (int i = 0; i < 1 << n; i ++)
for (int j = 0; j < n; j ++)
dp[i][j] = INF;
dp[1][0] = 0;
// 更新 dp 数组
for (int i = 0; i < 1 << n; i ++)
for (int j = 0; j < n; j ++)
if((i >> j & 1) == 1) // 如果 j 包含在 集合 i 中
for (int k = 0; k < n; k ++)
// k在集合i中,且k != j尝试用 k 村庄作为中转站来缩短距离
if(((i - (1 << j)) >> k & 1) == 1)
dp[i][j] = Math.min(dp[i][j], dp[i - (1 << j)][k] + g[k][j]);
int ans = INF;
for (int i = 1; i < n; i ++)
ans = Math.min(ans, dp[(1 << n) - 1][i] + g[i][0]);
System.out.printf("%.2f",(double)ans / 10000);
}
public static double get_distance(int i, int j) {
int x = p[i][0] - p[j][0];
int y = p[i][1] - p[j][1];
return Math.sqrt(x * x + y * y);
}
旅行商问题:
https://blog.youkuaiyun.com/qq_39559641/article/details/101209534?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164217200816780255284783%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=164217200816780255284783&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2alltop_positive~default-1-101209534.first_rank_v2_pc_rank_v29&utm_term=%E6%97%85%E8%A1%8C%E5%95%86%E9%97%AE%E9%A2%98&spm=1018.2226.3001.4187
题J:质数行者
题目:
小蓝在玩一个叫质数行者的游戏。
游戏在一个 n × m × w 的立体方格图上进行,从北到南依次标号为第 1 行到第 n 行,从西到东依次标号为第 1 列到第 m 列,从下到上依次标号为第 1 层到第 w 层。
小蓝要控制自己的角色从第 1 行第 1 列第 1 层移动到第 n 行第 m 列第 w层。每一步,他可以向东走质数格、向南走质数格或者向上走质数格。每走到一个位置,小蓝的角色要稍作停留。
在游戏中有两个陷阱,分别为第 r1 行第 c1 列第 h1 层和第 r2 行第 c2 列第h2 层。这两个陷阱的位置可以跨过,但不能停留。也就是说,小蓝不能控制角色某一步正好走到陷阱上,但是某一步中间跨过了陷阱是允许的。
小蓝最近比较清闲,因此他想用不同的走法来完成这个游戏。所谓两个走法不同,是指小蓝稍作停留的位置集合不同。
请帮小蓝计算一下,他总共有多少种不同的走法。
提示:请注意内存限制,如果你的程序运行时超过内存限制将不得分。
输入输出:
输入第一行包含两个整数 n, m, w,表示方格图的大小。
第二行包含 6 个整数,r1, c1, h1, r2, c2, h2,表示陷阱的位置。
输出一行,包含一个整数,表示走法的数量。答案可能非常大,请输出答案除以 1000000007 的余数。
样例输入
5 6 1
3 4 1 1 2 1
样例输出
11
样例说明
用 (r, c, h) 表示第 r 行第 c 列第 h 层,可能的走法有以下几种:
1. (1, 1, 1) ) (1, 3, 1) ) (1, 6, 1) ) (3, 6, 1) ) (5, 6, 1)。
2. (1, 1, 1) ) (1, 3, 1) ) (3, 3, 1) ) (3, 6, 1) ) (5, 6, 1)。
3. (1, 1, 1) ) (1, 3, 1) ) (3, 3, 1) ) (5, 3, 1) ) (5, 6, 1)。
4. (1, 1, 1) ) (3, 1, 1) ) (3, 3, 1) ) (3, 6, 1) ) (5, 6, 1)。
5. (1, 1, 1) ) (3, 1, 1) ) (3, 3, 1) ) (5, 3, 1) ) (5, 6, 1)。
6. (1, 1, 1) ) (3, 1, 1) ) (5, 1, 1) ) (5, 3, 1) ) (5, 6, 1)。
7. (1, 1, 1) ) (3, 1, 1) ) (5, 1, 1) ) (5, 4, 1) ) (5, 6, 1)。
8. (1, 1, 1) ) (1, 4, 1) ) (1, 6, 1) ) (3, 6, 1) ) (5, 6, 1)。
9. (1, 1, 1) ) (1, 6, 1) ) (3, 6, 1) ) (5, 6, 1)。
10. (1, 1, 1) ) (3, 1, 1) ) (3, 6, 1) ) (5, 6, 1)。
11. (1, 1, 1) ) (3, 1, 1) ) (5, 1, 1) ) (5, 6, 1)。
规模
对于 30% 的评测用例 1 ≤ n, m,w ≤ 50。
对于 60% 的评测用例 1 ≤ n, m,w ≤ 300。
对于所有评测用例,1 ≤ n, m, w ≤ 1000,1 ≤ r1,r2 ≤ n, 1 ≤ c1, c2 ≤ m, 1 ≤ h1, h2 ≤ w,陷阱不在起点或终点,两个陷阱不同。
分析一:动态规划
1000*1000*1000*4 = 4GB
300*300*300*4 = 100000000 = 100MB
dp[i][j][k]:表示从原点走到(i,j,k)位置的不同走法
有递推关系:
dp[i][j][k] = ∑dp[i-x][j][k] + ∑dp[i][j-y][k] + ∑dp[i][j][k-z]
x依次取小于等于i的所有质数、y、z同理。
这种方法,最多拿40分。
代码一:
import java.util.Scanner;
public class Main {
static int n,m,w,r1,c1,h1,r2,c2,h2;
static int M = 1000000007 ;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
n = in.nextInt();m = in.nextInt();w = in.nextInt();
r1 = in.nextInt();c1 = in.nextInt();h1 = in.nextInt();
r2 = in.nextInt();c2 = in.nextInt();h2 = in.nextInt();
int[][][] dp = new int[n+1][m+1][w+1];
int max = n;
max = Math.max(max, m);
max = Math.max(max, w);
int cnt = 0;
int[] p = new int[max+1];
int[] f = new int[max+1];
for(int i=2;i<=max;i++) {
if(f[i]==0) p[cnt++] = i;
for(int j=0;j<cnt&&i*p[j]<=max;j++) {
f[i*p[j]]=1;
if(i%p[j]==0) break;
}
}
dp[1][1][1]=1;
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
for(int k=1;k<=w;k++) {
for(int l=0;l<cnt;l++) {
if(i==r1&&j==c1&&k==h1) continue;
if(i==r2&&j==c2&&k==h2) continue;
if(i-p[l]>=1) dp[i][j][k]=(dp[i][j][k]+dp[i-p[l]][j][k])%M;
if(j-p[l]>=1) dp[i][j][k]=(dp[i][j][k]+dp[i][j-p[l]][k])%M;
if(k-p[l]>=1) dp[i][j][k]=(dp[i][j][k]+dp[i][j][k-p[l]])%M;
}
}
}
}
System.out.println(dp[n][m][w]);
}
}
分析二:
设dp[i][j]:表示从 1 走 j 步走到位置 i 的方案数。i <= 1000, j <= i/2。
从这个dp数组出发求解这个问题。
我们先不考虑经过两个特殊点的情况。
假设第一维我们走x步,第二维我们走y步,第三维我们走z步。
对应的dp数组中的值是:dp[n][x]、dp[m][y]、dp[w][z]
设 P = dp[n][x] * dp[m][y] * dp[w][z]
则这种情况下方案数为:
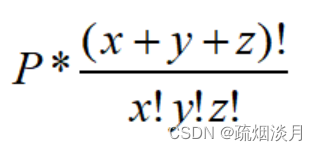
对于每一组x,y,z都有这么多方案数。
所以需要统计方案数。
如果是暴力的话是O(n^3)
可以先合并第二维和第三维。
用tmp[i]保存第二维和第三维共走了 i 步的方案数,然后再把第一维合并进来。
这样可以将时间降至O(n^2)。
注意:
a*b % M = a%M * b%M
a/b % M != a%M / b%M
需要用到逆元的概念。
设 a / b % M = a * c % M,则 c 是 b 的逆元。
当M为质数时,可以用费马小定理求逆元
即:c = b ^ (M-2)
因为M是个非常大的数,所以需要用快速幂来计算。
代码二:
static int mod = 1000000007;
static int maxn = 1010;
static long dp[][],vis[][],jc[],inv[],tmp[];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n,m,w,r1,c1,h1,r2,c2,h2;
n = sc.nextInt(); m = sc.nextInt(); w = sc.nextInt();
r1 = sc.nextInt(); c1 = sc.nextInt(); h1 = sc.nextInt();
r2 = sc.nextInt(); c2 = sc.nextInt(); h2 = sc.nextInt();
dp = new long[maxn][maxn]; // dp[i][j] 表示从 1 走 j 走到位置 i 的方案数
vis = new long[maxn][maxn];
jc = new long[maxn<<1]; // jc[i] 存放的是 i!
inv = new long[maxn<<1];//inv[i] 存放的是 i! 的逆元
int[] primes = ola(maxn);
jc[0] = 1; inv[0] = 1; inv[1] = 1;
for(int i=1;i< 2000;i++) jc[i] = (jc[i-1]*i) % mod;
for(int i=2;i< 2000;i++) inv[i]=quickPower(jc[i],mod-2);// 费马小定理求阶乘逆元
dp[1][0]=1;vis[1][0]=1;
int up = max(n,max(m,w)), now = 0;
for (int i = 2; i <= up; i++){
for (int j = 0; j <= now; j++){
for (int k = 0; k < primes.length; k++){
if (i-primes[k] < 1)break;
if (vis[i-primes[k]][j] == 0) continue;
dp[i][j+1]=(dp[i][j+1]+dp[i-primes[k]][j])%mod;
vis[i][j+1]=1;
}
}
if (vis[i][now+1] != 0) now++;
}
long ans=calc(n,m,w);
ans=(ans-(calc(r1,c1,h1)*calc(n-r1+1,m-c1+1,w-h1+1))%mod+mod)%mod;
ans=(ans-(calc(r2,c2,h2)*calc(n-r2+1,m-c2+1,w-h2+1))%mod+mod)%mod;
if (r1<=r2&&c1<=c2&&h1<=h2)ans=(ans+calc(r1,c1,h1)*calc(r2-r1+1,c2-c1+1,h2-h1+1)%mod*calc(n-r2+1,m-c2+1,w-h2+1)%mod)%mod;
if (r2<=r1&&c2<=c1&&h2<=h1)ans=(ans+calc(r2,c2,h2)*calc(r1-r2+1,c1-c2+1,h1-h2+1)%mod*calc(n-r1+1,m-c1+1,w-h1+1)%mod)%mod;
System.out.println(ans);
}
static long calc(int x,int y,int z){ // 从(1,1,1)出发到达(x,y,z)的方案数
tmp = new long[maxn<<1];
for (int i=0;i<=y;i++){
for (int j=0;j<=z;j++){
tmp[i+j] += (((dp[y][i]*dp[z][j]%mod)*jc[i+j]%mod)*inv[i]%mod)*inv[j]%mod;
tmp[i+j] %= mod;
}
}
//合并二三维
long ans=0;
for (int i=0;i<=x;i++){
for (int j=0;j<=y+z;j++){
ans += (((dp[x][i]*tmp[j]%mod)*jc[i+j]%mod)*inv[i]%mod)*inv[j]%mod;
ans %= mod;
}
}
return ans;
}
// 使用欧拉筛寻找小于n的所有素数
public static int[] ola(int n){
int cnt = 0; // 质数的个数
int[] primes = new int[n+1]; // 用于存储质数
int[] st = new int[n+1];
for(int i = 2; i <= n; i++) {
if(st[i] == 0) primes[cnt++] = i;
for(int j = 0; primes[j] <= n / i; j++) {
st[primes[j]*i] = 1;
if(i % primes[j] == 0) break;
}
}
int[] ans = new int[cnt];
for (int i = 0; i < ans.length; i++) {
ans[i] = primes[i];
}
return ans;
}
public static int max(int a, int b) {
return Math.max(a, b);
}
static long quickPower(long a,long b){
long ans=1;
a %= mod;
while(b>0){
if(b%2==1) ans=(ans*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return ans;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








