10-SVM

• 点到超平面的距离
  设n维空间的超平面方程为：$w^{T}x+b=0$， 其中w是这个超平面的法向量$w=(w_1,w_2,w_3,..{)}^T$, 有点x0到超平面的距离为：
  $$\frac{|w^T{x}_0+b|}{||w||}$$
  推导过程：
  令x’是超平面上的一点，点x到超平面的距离就是向量（x-x’）在法线方向上的投影，即 ||x-x’||cos(a) ,a是（x-x’）与法向量的夹角。我们知道两个向量的內积$w^T(x-x^{\prime })=||w||.||(x-x^{\prime })||.cos(a)$,所以有 点到超平面的距离d
  $$d=\frac{w^T(x-x^{\prime })}{||w||}$$
  x’ 满足$w^{T}x+b=0$ ，所有
  $$d=\frac{w^{T}x+b}{||w||}$$

• 变形：两个平行超平面之间的距离
  $w^T{x}_1+b=1$, $w^T{x}_2+b=-1$ 是两个平行的超平面，则这两个平面的距离是$\frac{2}{||w||}$
  $$w^T(x_1-x_2)=2$$
  $$\frac{w^T(x_1-x_2)}{||w||}=\frac{2}{||w||}$$

支持向量机

• 目标是最大化 $\frac{2}{||w||}$ 同时保证所有样本正确分类 , w是超平面的参数。样本正确分类 等价于 满足等式 $y_i(\sum w_i{x}_i+b)>=1$.
• 最大化$\frac{2}{||w||}$ 可以等价为 最小化$1/2||w|{|}^2$, 最小化$1/2||w|{|}^2$会使问题变得简单。
• 类似于 最小化w的长度的平方，并限制于某些条件 这种形式的最优化问题 称为二次规划(quadratic programming)问题。
  求解二次规划问题，人们已经有了直截了当的方式。
• 还可以将上面二次规划问题再次转化为 标准的二次规划的问题形式。最大化$W(\alpha )$ ,$\alpha$是新参数
  $$W(\alpha )=\sum _i\alpha -1/2\sum _{i,j}{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
  $$st.{\alpha }_i>0,\sum _i{\alpha }_i{y}_i=0$$
• 找到最大化这个方程的$\alpha$后，可以还原原方程的w参数（超平面的参数）：$w={\sum }_i{\alpha }_i{x}_i{y}_i$
• 绝大部分的 ${\alpha }_i$都是 0 ，${\alpha }_i$不为0的那些点就被称为支持向量

核函数

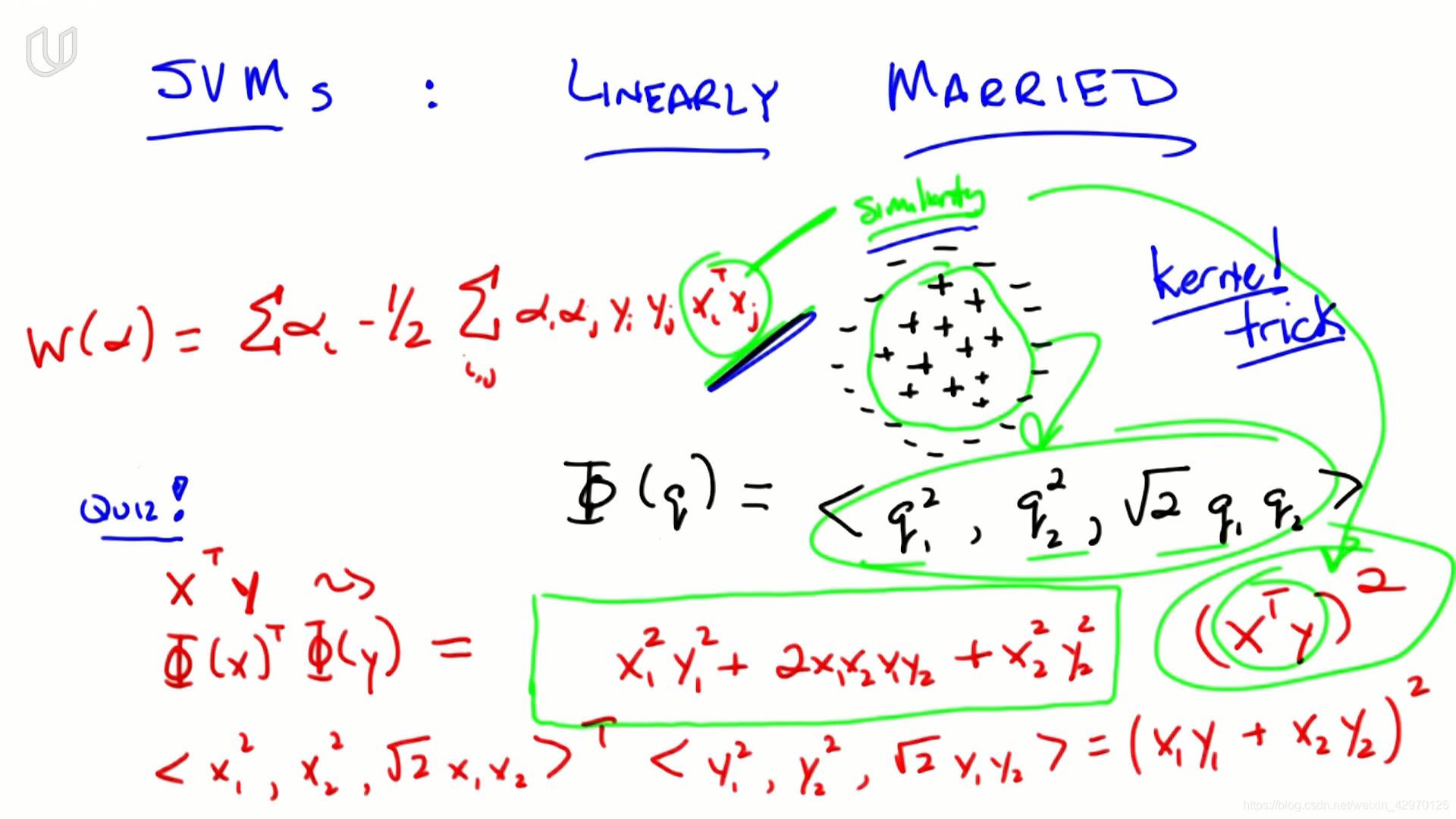
• 向量q 在平面上，因而它有两个分量(q1,q2),利用q 产生一个三维向量：
  $$\Phi (q)=<q_1^2,q_2^2,\sqrt{2}{q}_1{q}_2>$$
  这个过程实际上并没有增加新的信息。
• 将这些点从两个维度投影到三个维度，基本上获得所有正点并将它们沿第三个维度上移，所有的负点下移，这样就可以用超平面分割
• 內积是我们定义相似度similarity的方式，
• 将数据投影到更高维度的空间中，在那里进行比较，只需对算法做一点小小改变。点积可以转化成其他相似性度量，称之为核函数：$x_i^T{x}_j$ -->$K(x_i,x_j)$
• 核函数必须满足mercer condition

11-SVM

• 增加一个新特征 $z=x^2+y^2$, SVM能够以圆的形式学习出非线性的决策边界

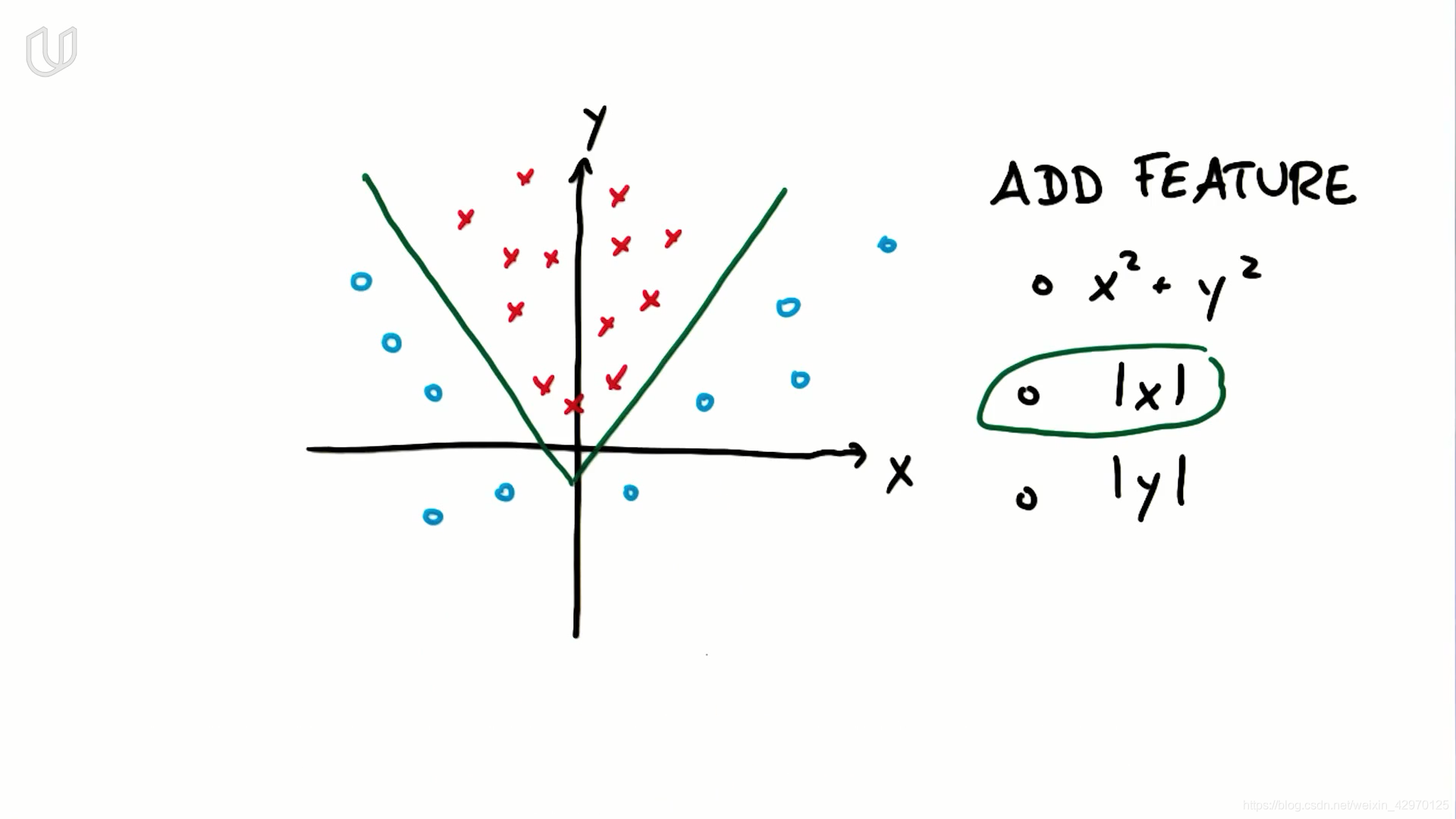
• 对于以上数据集，应增加新特征 |x|

class sklearn.svm.SVC(C=1.0, kernel=’rbf’, degree=3, gamma=’auto_deprecated’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=’ovr’, random_state=None)

gamma : float, optional (default=’auto’)
Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.

• 参数C: 决策边界的平滑度和训练数据分类的正确性 的折中，C的值越大，越偏向分类的正确性，越不能容忍出现误差,容易过拟合
• 参数gamma：gamma是选择RBF函数作为kernel后，该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多。支持向量的个数影响训练与预测的速度

拉格朗日乘子法

拉格朗日乘数法是 求多元函数在在其变量受到一个或多个约束条件下的极值的方法。通过引入拉格朗日算子，将d个变量，k个约束条件的最优化问题转化为k+d个变量的无约束优化问题。

无约束优化

对于变量 $x\in {\mathbb{R}}^N$的函数 f(x) ,无约束优化问题如下:$$\underset{x}{\min }f(x)$$
根据 Fermat 定理，直接找到使目标函数得 0 的点即可 即 ${\nabla }_{x}f(x)=0$ ，如果没有解析解的话，可以使用梯度下降或牛顿方法等迭代的手段来使 x 沿负梯度方向逐步逼近极小值点。

等式约束优化

当目标函数加上约束条件之后，问题就变成如下形式：
$$\underset{x}{\min }f(x)$$
$$s.t.h_i(x)=0,i=1,2,...,m$$

• 约束条件会将解的范围限定在一个可行域，此时不一定能找到使得${\nabla }_{x}f(x)$为 0 的点，只需找到在可行域内使得 f(x) 最小的值即可
• 常用的方法即为拉格朗日乘子法，该方法首先引入拉格朗日乘子( Lagrange Multiplier) $\alpha \in {\mathbb{R}}^m$ ，构建 Lagrangian 如下：
  $$L(x,\alpha )=f(x)+\sum _i^m{\alpha }_{i}h(x)$$
• 绿线是约束条件h(x),在最优点处，h(x)的法向量（梯度）与f(x)的法向量必定平行（即两者相切），于是有（或+）：$${\nabla }_{x}f(x)-\alpha {\nabla }_{x}h(x)=0$$
  
• 求解：（其中 ${\nabla }_{\alpha }L(x,\alpha )=h(x)=0$即约束条件）
  $$\{\begin{array}{ll}{\nabla }_{x}L(x,\alpha )=0& \\ {\nabla }_{\alpha }L(x,\alpha )=0& \end{array}$$
  那么一个带等式约束的优化问题就通过拉格朗日乘子法转化成无约束的优化问题求解

不等式约束优化

• 任何原始问题约束条件无非最多3种，等式约束，大于号约束，小于号约束，而这三种最终通过将约束方程化简化为两类：约束方程等于0和约束方程小于0
• 不等式约束优化:
  $$\underset{x}{\min }f(x)$$
  $$\begin{gathered} s.t. \\ h(x)\le 0 \end{gathered}$$
• 拉格朗日函数为：$L(x,\lambda )=f(x)+\lambda h(x)$
• 当可行解 x 落在 g(x)<0 的区域内，此时直接极小化 f(x) 即可,即约束条件不起作用，即$\lambda =0$
• 当可行解 x 落在 g(x)=0 即边界上，此时等价于等式约束优化问题。即$h(x)=0$
• 于是有： $\lambda h(x)=0$
• 在等式约束优化中，约束函数与目标函数的梯度只要满足平行即可，而在不等式约束中则不然，若 λ≠0，这便说明 可行解 x 是落在约束区域的边界上的，这时可行解应尽量靠近无约束时的解
• 梯度方向就是函数值增大的方向，我们的目标是要最小化目标函数，如果最优解在约束边界上，表明g(x)<0 的区域内的目标函数的值要大于目标函数在边界上的值，所以目标函数的梯度应该与约束函数的梯度方向相反，有:$$\begin{gathered} f(x)+\lambda h(x)=0 \\ \lambda >0 \end{gathered}$$
  
• 形式化的不等式约束优化问题：$$\begin{array}{rl}& \underset{x}{\min }f(x)\\ & s.t.h_i(x)=0,i=1,2,...,m\\ & g_j(x)\le 0,j=1,2,...,n\end{array}$$
• 列出 Lagrangian 得到无约束优化问题:
  $$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^m{\alpha }_i{h}_i(x)+\sum _{j=1}^n{\beta }_i{g}_i(x)$$
• 加上不等式约束后可行解 x 需要满足的就是以下的 KKT 条件：
  $$\begin{array}{rl}{\nabla }_{x}L(x,\alpha ,\beta )& =0\\ {\beta }_j{g}_j(x)& =0,j=1,2,...,n\\ h_i(x)& =0,i=1,2,...,m\\ g_j(x)& \le 0,j=1,2,...,n\\ {\beta }_j& \ge 0,j=1,2,...,n\end{array}$$

例子

• 等式约束:

  • 1 问题
    $$\begin{gathered} minf=2x_1^2+3x_2^2+7x_3^2 \\ s.t.2x_1+x_2=1 \\ 2x_2+3x_3=2 \end{gathered}$$
  • 2
    $$minf=2x_1^2+3x_2^2+7x_3^2+{\alpha }_1(2x_1+x_2-1)+{\alpha }_2(2x_2+3x_3-2)$$
  • 3
    $$\begin{gathered} \frac{\partial f}{\partial x_1}=4x_1+2{\alpha }_1=0\Rightarrow x_1=-0.5{\alpha }_1 \\ \frac{\partial f}{\partial x_2}=6x_2+{\alpha }_1+2{\alpha }_2=0\Rightarrow x_2=-\frac{{\alpha }_1+2{\alpha }_2}{6} \\ \frac{\partial f}{\partial x_3}=14x_3+3{\alpha }_2=0\Rightarrow x_3=-\frac{3{\alpha }_2}{14} \end{gathered}$$
  • 4 把它在代到约束条件中去，可以看到，2个变量两个等式，可以求解，最终可以得到${\alpha }_1=-0.39,{\alpha }_2=-1.63$

• 不等式约束:

  • 1 问题：$$\begin{gathered} minf=x_1^2-2x_1+1+x_2^2+4x_2+4 \\ s.t.x_1+10x_2>10 \\ 10x_1-10x_2<10 \end{gathered}$$
  • 2 $$\begin{gathered} L(x,\alpha )=f(x)+{\alpha }_{1}g1(x)+{\alpha }_{2}g2(x) \\ =x_1^2-2x_1+1+x_2^2+4x_2+4+{\alpha }_1(10-x_1-10x_2)+ \\ {\alpha }_2(10x_1-x_2-10) \end{gathered}$$
  • 3 此时分别对x1、x2求导数：$$\begin{gathered} \frac{\partial L}{\partial x_1}=2x_1-2-{\alpha }_1+10{\alpha }_2=0\Rightarrow x_1=0.5({\alpha }_1-10{\alpha }_2+2) \\ \frac{\partial L}{\partial x_2}=2x_2+4-10{\alpha }_1-{\alpha }_2=0\Rightarrow x_2=0.5(10{\alpha }_1+{\alpha }_2-4) \end{gathered}$$
  • 4 还有一个条件就是α∗g(x)=0,那么也就是$$\begin{gathered} {\alpha }_1\ast g_1(x)={\alpha }_1\ast (10-x_1-10x_2)=0 \\ {\alpha }_2\ast g_2(x)={\alpha }_2\ast (10x_1-x_2-10)=0 \end{gathered}$$
  • （1）α1=α2=0α1=α2=0，那么看上面的关系可以得到x1=1,x2=−1x1=1,x2=−1,再把两个x带到不等式约束，发现第一个就是需要满足（10-1+20=29<0)显然不行，29>0的。舍弃
    （2）g1(x)=g2(x)=0g1(x)=g2(x)=0，带进去解得，x1=110/101;x2=90/101,再带回去求解α1，α2α1，α2，发现α1=58/101，α2=4/101α1=58/101，α2=4/101，它们满足大于0的条件，那么显然这组解是可以的。
    （3）其他两种情况再去讨论发现是不行的。

拉格朗日对偶

$$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^m{\alpha }_i{h}_i(x)+\sum _{j=1}^n{\beta }_i{g}_i(x)$$
因为 $h_i(x)\le 0,\alpha \ge 0,g_i(x)=0$,所以如果把$L(x,\alpha ,\beta )$ 看作是${\alpha }_i,{\beta }_i$的函数，有：
$$\underset{\alpha ,\beta :{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )=\{\begin{array}{ll}f(x),& \text{if x 满足原始问题约束}\\ +\infty ,& \text{if 其他}\end{array}$$

• 原问题(primal problem): $$p^{\ast }=\underset{x}{\min }\underset{\alpha ,\beta }{\max }L(x,\alpha ,\beta )$$
• 对偶问题（dual problem）:$$d^{\ast }=\underset{\alpha ,\beta }{\max }\underset{x}{\min }L(x,\alpha ,\beta )$$
• 通常，$p^{\ast }\ge d^{\ast }$ 即对偶问题的最优解是原始问题最优解的下限（弱对偶性）
• 但如果是满足KKT条件的方程组的解$$\begin{array}{rl}{\nabla }_{x,\alpha ,\beta }L(x,\alpha ,\beta )& =0\\ {\beta }_j{g}_j(x)& =0,j=1,2,...,n\\ g_j(x)& \le 0,j=1,2,...,n\\ {\beta }_j& \ge 0,j=1,2,...,n\end{array}$$
  此时，$p^{\ast }=d^{\ast }$强对偶性，原始问题和对偶问题的最优解严格相等
  当f(x)和g(x)为凸函数，h(x)为仿射函数时，p*= d*
• 因为 $\beta g(x)=0$,即$L(x,\alpha ,\beta )=f(x)$，所以具有强对偶性

支持向量机的对偶

• 支持向量机最大间隔化下的损失函数：
  $$\begin{gathered} \min \frac{1}{2}||w|{|}^2 \\ s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2,...,m \end{gathered}$$
  约束条件可以写成：
  $$g_i(\mathbf{w})=1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\le 0$$
• 构造拉格朗日函数： $$L(\mathbf{w},b,\lambda )=\frac{1}{2}||w|{|}^2+\sum _i^m{\lambda }_i(1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b))$$
• 对偶问题的形式，先求$L(\mathbf{w},b,\lambda )$对w,b的极小，再求对$\lambda$的极大
  • 1 求${\min }_{w,b}L(\mathbf{w},b,\lambda )$,将拉格朗日函数分别对 w，b 求偏导并令其等于0：
    $$\begin{gathered} {\nabla }_{w}L(\mathbf{w},b,\lambda )=\mathbf{w}-\sum _i^m{\lambda }_i{y}_i{\mathbf{x}}_i=0, \\ \mathbf{w}=\sum _i^m{\lambda }_i{y}_i{\mathbf{x}}_i \\ {\nabla }_{b}L(\mathbf{w},b,\lambda )=\sum _i^m{\lambda }_i{y}_i=0 \end{gathered}$$
  • 2 将以上求得代入拉格朗日函数：
    $$\begin{gathered} L(\mathbf{w},b,\lambda )=\frac{1}{2}||w|{|}^2+\sum _i^m{\lambda }_i(1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)) \\ =\frac{1}{2}\sum _i^m\sum _j^m{\lambda }_i{\lambda }_j{y}_i{y}_j({\mathbf{x}}_i\cdot {\mathbf{x}}_j)+\sum _i^m{\lambda }_i-\sum _i^m\sum _j^m{\lambda }_i{\lambda }_j{y}_i{y}_j({\mathbf{x}}_i\cdot {\mathbf{x}}_j) \\ =-\frac{1}{2}\sum _i^m\sum _j^m{\lambda }_i{\lambda }_j{y}_i{y}_j({\mathbf{x}}_i\cdot {\mathbf{x}}_j)+\sum _i^m{\lambda }_i \end{gathered}$$
  • 3 以上得出的式子就是$L(\mathbf{w},b,\lambda )$对w，b的极小:$mi{n}_{\mathbf{w},b}L(\mathbf{w},b,\lambda )$;下面需要继续求这个式子对$\lambda$的极大：
    $$\underset{\lambda }{\max }W(\lambda )=\underset{\lambda }{\max }-\frac{1}{2}\sum _i^m\sum _j^m{\lambda }_i{\lambda }_j{y}_i{y}_j({\mathbf{x}}_i\cdot {\mathbf{x}}_j)+\sum _i^m{\lambda }_i$$
    或可以将求极大转换为求极小：
    $$\underset{\lambda }{\min }W(\lambda )=\underset{\lambda }{\min }\frac{1}{2}\sum _i^m\sum _j^m{\lambda }_i{\lambda }_j{y}_i{y}_j({\mathbf{x}}_i\cdot {\mathbf{x}}_j)-\sum _i^m{\lambda }_i$$
    $$\begin{gathered} s.t.\sum _i^m{\lambda }_i{y}_i=0 \\ \lambda \ge 0,i=1,2,...,m \end{gathered}$$
    并且满足KKT条件$$\begin{gathered} 1-y_{i}f({\mathbf{x}}_i)\le 0 \\ \lambda (1-y_{i}f({\mathbf{x}}_i))=0 \\ \lambda \ge 0 \end{gathered}$$

线性可分支持向量机的学习算法 r4p106

输入：线性可分训练集 T={(x1,y1),(x2,y2),...,(xm,ym),}T=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m),\}T={(x1​,y1​),(x2​,y2​),...,(xm​,ym​),},其中xu∈Rn,y∈{−1,1},i=1,2,...,mx_u \in\R^n,y\in\{-1,1\},i=1,2,...,mxu​∈Rn,y∈{−1,1},i=1,2,...,m
输出：分离超平面和分类决策函数
1） 构造并求解约束最优化问题
$$\begin{gathered} \underset{\lambda }{\min }W(\lambda )=\underset{\lambda }{\min }\frac{1}{2}\sum _i^m\sum _j^m{\lambda }_i{\lambda }_j{y}_i{y}_j({\mathbf{x}}_i\cdot {\mathbf{x}}_j)-\sum _i^m{\lambda }_i \\ s.t.\sum _i^m{\lambda }_i{y}_i=0 \\ \lambda \ge 0,i=1,2,...,m \end{gathered}$$
求得最优解 ${\lambda }^{\ast }=({\lambda }_1^{\ast },{\lambda }_2^{\ast }),...,{\lambda }_m^{\ast })$

这是一个二次规划问题，可通过二次规划算法求解；然而该问题的规模正比于训练样本数，在实际任务中会有很大的开销
SMO（Sequential Minimal Optimization）算法是解决这个问题的一个高效的算法

2. 计算$${\mathbf{w}}^{\ast }=\sum _i^m{\lambda }_i^{\ast }{y}_i{\mathbf{x}}_i$$
   选取${\lambda }^{\ast }$的任一正分量${\lambda }_j^{\ast }>0$,计算$$b^{\ast }=y_j-\sum _i^m{\lambda }_i{y}_i(x_i\cdot x_j)$$

$b^{\ast }$的求解过程：
在最优解 ${\lambda }^{\ast }$中至少有一个${\lambda }_j^{\ast }>0$,根据KKT条件$\lambda (1-y_{i}f({\mathbf{x}}_i))=0$ 有：
$$\begin{gathered} {\lambda }_j(1-y_j(\mathbf{w}\cdot {\mathbf{x}}_j+b))=0 \\ 1-y_j(\sum _i^m{\lambda }_i{y}_i({\mathbf{x}}_i\cdot {\mathbf{x}}_j)+b)=0 \end{gathered}$$
因为总有$y_j^2=1$
所以：$$b=y_j-\sum _i^m{\lambda }_i{y}_i({\mathbf{x}}_i\cdot {\mathbf{x}}_j)$$

3. 求得分离超平面：$${\mathbf{w}}^{\ast }\cdot \mathbf{x}+b^{\ast }=0$$
   分类决策函数：$$f(x)=sign({\mathbf{w}}^{\ast }\cdot \mathbf{x}+b^{\ast })$$

• 示例见r4p107
• 在最大化决策间隔时，必然有一些点落在间隔的边界上，这些点就是支持向量。有KKT条件$${\lambda }^{\ast }(y_i({\mathbf{w}}^{\ast }\cdot {\mathbf{x}}_i+b)-1)=0$$
  对于${\lambda }^{\ast }>0$的实例${\mathbf{x}}_i$,有$$y_i({\mathbf{w}}^{\ast }\cdot {\mathbf{x}}_i+b)-1=0$$ 或 $${\mathbf{w}}^{\ast }\cdot {\mathbf{x}}_i+b=\pm 1$$
  可见 支持向量是一定落在间隔边界上