深搜之N皇后问题

深度优先搜素(Depth First Serch):

其过程简而言之是对每一个分支路径深入到不能再深入位置，即沿一条路径不断的纵深，不撞南墙不回头。

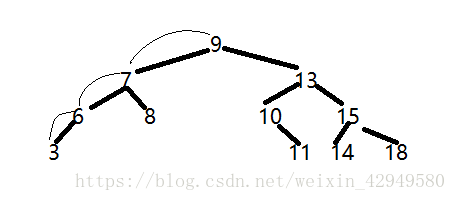
也就是加入我们要寻找8这个数字，首先，它会9->7->6->3一直到最后一个，发现并没有寻找到8，那么我们再返回3->6，还是没有8，我们继续返回3->6->7,发现7还有一个岔路，那么我们就从7->8，这样即完成了寻找。

---

深搜之N皇后问题：

在N*N的方格棋盘放置了N个皇后，使得它们不相互攻击（即任意2个皇后不允许处在同一排，同一列，也不允许处在与棋盘边框成45角的斜线上。
你的任务是，对于给定的N，求出有多少种合法的放置方法。

Input
共有若干行，每行一个正整数N≤10，表示棋盘和皇后的数量；如果N=0，表示结束。
Output
共有若干行，每行一个正整数，表示对应输入行的皇后的不同放置数量。
Sample Input
1
8
5
0
Sample Output
1
92
10
题目分析： 首先任意皇后不能处于同一行，同一列，主副对角线上，那么也就是说我们每一行是只能是一个皇后的。那我们就固定行，从第一行之第N行，逐列寻找满足条件的位置去放上皇后即可了。但是这条题必须得打表，也就是说必须把1~10的行的可能放置种类都存在数组当中，因为如果测试样例是 10 10 10…你没有必要每次算一遍，所以存在数组当中，直接调用就行。

/*
对于皇后问题这道题，要明白是不能在同一列同一行放皇后，也就是说
一行只能有一个皇后，固定行数之后只要对列遍历即可。
*/
#include <bits/stdc++.h>

using namespace std;

int mark[11][11];//我们从第一行第一列开始，这是标记
int cnt[11];//打表计数
int N;//棋盘和皇后的数量
int Count;
void dfs(int row);
bool isCorrect(int R,int C);

int main(){
    //我们将棋盘由1~10的所有所有可能的存在打表的数组当中
    for(N=1;N<=10;N++){
        dfs(1);//从第一行开始
        cnt[N]=Count;
        Count=0;
    }
    while(~scanf("%d",&N)&&N){
        cout << cnt[N] <<endl;
    }
    return 0;
}
void dfs(int row){
    if(row==N+1){
        Count++;//也就是前1~N行，每个位置都正确的放入了皇后，那么次数就+1
        return;
    }
    else{
        //循环的意思是，我们已知行是row行了，
        //那么我们只需要从第一列到第N列中选择正确的一列即可
        for(int i=1;i<=N;i++){
            if(isCorrect(row,i)){
                mark[row][i]=1;//如果这个位置可以放置皇后，那么我们把它标记为1
                dfs(row+1);//之后进行下一行的搜索，
                           //dfs会一直纵深，直到停止，return
                mark[row][i]=0;
                //当dfs return返回后，说明这一条支路已经走完，
                //那么我们把此位置标记为0，进行下一个可能性的判断
                //每次深搜之后整个mark数组都会重新归为0
            }
        }
    }
    return;
}
bool isCorrect(int R,int C){
    /*
    我们将前1~R行，进行遍历，看是否满足条件，因为R~N行，并没有放任何皇后
    那么他们本身就是满足条件的
    */
    for(int i=1;i<=R;i++){
        for(int j=1;j<=N;j++){
            if(i+j==R+C&&mark[i][j]==1)return false;//在主对角线上，满足规律i+j=R+C
            if(C-R==j-i&&mark[i][j]==1)return false;//在副对角线上
            //在同一列当中
            if(j==C&&mark[i][j]==1)return false;
        }
    }
    return true;
}