高斯过程与核函数详解-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_42927835/article/details/119305192

8.1 学习论文
逐句弄懂，打好基础，不急于求成，日积月累加油！

置信区间和置信度
正态分布(Normal distribution)，也叫高斯分布。若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
高斯过程（GP）是概率论和数理统计中随机过程的一种，是一系列服从正态分布的随机变量在一指数集（index set）内的组合。高斯过程由其数学期望和协方差函数完全决定，并继承了正态分布的诸多性质 [1] 。
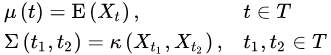
核函数（kernel function）
高斯过程的性质与其协方差函数有密切联系，在构造高斯过程时，一些特定形式的协方差函数被称为核函数。核函数的选择要求满足Mercer定理，即核函数在样本空间内的任意格拉姆矩阵（Gram matrix）为半正定矩阵。这里对高斯过程常见的核函数类型进行总结。
核函数的两个重要度量是单调性和平滑性（smoothness）。表中的核函数均是单调递减函数，因此样本间的相关性与样本间距离成反比，此时特征长度尺度越小，样本间的相关性越高。随机过程的平滑性由均方导数（mean squared derivative）描述，表中RBF核对应无限均方可导的平滑高斯过程；马顿核与RQ核的均方可导性与其超参数有关，例如在取1.5和2.5时，马顿核是1阶和2阶均方可导的；指数函数核对应的高斯过程是奥恩斯坦-乌伦贝克过程（Ornstein-Uhlenbeck Process, OU），OU过程是一个具有强马尔可夫性且均方不可导的随机过程（参见特例部分）。
各项同性（isotropy）与各向异性（anisotropy）核函数：
若高斯过程为高斯随机场，对应的指数集表示空间时，其核函数的选择有各向同性与各向异性之分。各向同性表示样本的协方差与其向量的方向无关，即仅与距离有关，各向异性反之。
平稳高斯过程的数学期望是一常数，因此由核函数完全定义。