选择排序--简单，堆排序

简单选择排序：每次在n-i个序列中选择出关键字的最小的，并和第i个元素进行交换。

• 时间复杂度为O(n2),空间复杂度为O(1),是不稳定排序。（红色的4排序前在黑色的4前面，但排序后红色的4在黑色的4后面，不稳定）
  

#include<iostream>
using namespace std;
//每次选出关键字最小的与之交换 
void SeletctSort(int a[],int length);//简单选择排序
int compare(int a[],int begin,int end);//查找关键字最小的，并返回下标  
void output(int a[],int length);//输出 
int main(){
	int a[6]={-1,3,4,5,2,1};
	SeletctSort(a,5);
	output(a,5);
}
void SeletctSort(int a[],int length){
	for(int i=1;i<=length;i++){
		int j=compare(a,i,length);
		if(i!=j){
			int temp=a[i];
			a[i]=a[j];
			a[j]=temp;
		} 
	}
} 
int compare(int a[],int begin,int end){
	int min=1000;
	int tag;//记录下标  
	for(int i=begin;i<=end;i++){
		if(a[i]<min){
			min=a[i];
			tag=i;
		}
	}
	return tag;
} 
void output(int a[],int length){
	for(int i=1;i<=length;i++)
		cout<<a[i]<<" ";
	cout<<endl;
} 

堆排序：

• 堆定义：

• 
  注： 类似于完全二叉树中所有非终端结点的值都大于（或小于）其左，右孩子结点的值。

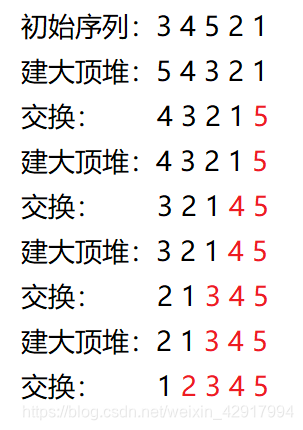
• 堆排序： 按照非降序的排序，要用大顶堆。首先对于无序序列进行建堆，然后将堆顶元素与最后一个元素交换（大顶堆的堆顶元素最大，放在最后面），然后将剩余的n-1个元素重新建立一个大顶堆。一直重复该过程，便可以得到有序序列。

• 时间复杂度为O(nlogn),空间复杂度为O(1),是不稳定排序。

• 例子：
  

#include<iostream>
using namespace std;
void HeapSort(int a[],int length);//堆排序 
void HeapAdujst(int a[],int s,int m);//堆调整 (大顶堆)
void output(int a[],int length);//输出  
int main(){
	int a[6]={-1,3,4,5,2,1};
	HeapSort(a,5);
	output(a,5);
}
void HeapSort(int a[],int length){
	for(int i=length/2;i>0;i--)//建大顶堆 
		HeapAdujst(a,i,length);
	for(int i=length;i>1;i--){
		int temp=a[i];
		a[i]=a[1];
		a[1]=temp;
		HeapAdujst(a,1,i-1);
	}
	
} 
void HeapAdujst(int a[],int s,int m){
	int temp=a[s];
	for(int j=2*s;j<=m;j=j*2){//前面的调整对后面的有影响
		if(a[j]<a[j+1]&&j+1<=m)	j++;
		if(temp>a[j]) //大的情况，不用交换 
			break;
		else{
			a[s]=a[j];
			s=j;
		}	
	}
	a[s]=temp;
}
void output(int a[],int length){
	for(int i=1;i<=length;i++)
		cout<<a[i]<<" ";
	cout<<endl;
} 

注：实质上建大顶堆的过程就是找最大值，只不过每次建大顶堆是从一半开始的，所以时间复杂度低。