部分转自:

斐波那契数列
1. 爬楼梯
70. Climbing Stairs (Easy)
题目描述:有 N 阶楼梯,每次可以上一阶或者两阶,求有多少种上楼梯的方法。
定义一个数组 dp 存储上楼梯的方法数(为了方便讨论,数组下标从 1 开始),dp[i] 表示走到第 i 个楼梯的方法数目。
第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达,走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。

考虑到 dp[i] 只与 dp[i - 1] 和 dp[i - 2] 有关,因此可以只用两个变量来存储 dp[i - 1] 和 dp[i - 2],使得原来的 O(N) 空间复杂度优化为 O(1) 复杂度。
//在线模拟
public int climbStairs(int n) {
if (n <= 2) {
return n;
}
int pre2 = 1, pre1 = 2;
for (int i = 2; i < n; i++) {
int cur = pre1 + pre2;
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
2. 强盗抢劫
198. House Robber (Easy)
题目描述:抢劫一排住户,但是不能抢邻近的住户,求最大抢劫量。
定义 dp 数组用来存储最大的抢劫量,其中 dp[i] 表示抢到第 i 个住户时的最大抢劫量。
由于不能抢劫邻近住户,如果抢劫了第 i -1 个住户,那么就不能再抢劫第 i 个住户,所以

class Solution {
public int rob(int[] nums) {
if(nums==null || nums.length==0) {
return 0;
}
if(nums.length<=2) {
return (nums.length==2) ? Math.max(nums[0],nums[1]) : nums[0];
}
int[] dp = new int[nums.length];
//如果只有一个元素那么最大值就是nums[0]
//如果有两个元素最大值就是max(nums[0],nums[1])
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
//利用前面两个位置的最大值计算本次的最大值
for(int i=2;i<nums.length;++i) {
dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]);
}
//最大值就在数组的最后一位
return dp[nums.length-1];
}
}
作者:wang_ni_ma
链接:https://leetcode-cn.com/problems/house-robber/solution/si-chong-jie-fa-xiang-xi-tu-jie-198-da-jia-jie-she/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
空间还可以 优化一下
public int rob(int[] nums) {
int pre2 = 0, pre1 = 0;
for (int i = 0; i < nums.length; i++) {
//pre1是抢了前一个的,pre2是抢了前前一个的
int cur = Math.max(pre2 + nums[i], pre1);
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
3. 强盗在环形街区抢劫
213. House Robber II (Medium)
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int n = nums.length;
if (n == 1) {
return nums[0];
}
return Math.max(rob(nums, 0, n - 2), rob(nums, 1, n - 1));
}
private int rob(int[] nums, int first, int last) {
int pre2 = 0, pre1 = 0;
for (int i = first; i <= last; i++) {
int cur = Math.max(pre1, pre2 + nums[i]);
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
4. 信件错排
(这个思路太厉害了,我们的动态规划,行!)
题目描述:有 N 个 信 和 信封,它们被打乱,求错误装信方式的数量。
定义一个数组 dp 存储错误方式数量,dp[i] 表示前 i 个信和信封的错误方式数量。假设第 i 个信装到第 j 个信封里面,而第 j 个信装到第 k 个信封里面。根据 i 和 k 是否相等,有两种情况:
- i==k,交换 i 和 j 的信后,它们的信和信封在正确的位置,但是其余 i-2 封信有 dp[i-2] 种错误装信的方式。由于 j 有 i-1 种取值,因此共有 (i-1)*dp[i-2] 种错误装信方式。
- i != k,交换 i 和 j 的信后,第 i 个信和信封在正确的位置,其余 i-1 封信有 dp[i-1] 种错误装信方式。由于 j 有 i-1 种取值,因此共有 (i-1)*dp[i-1] 种错误装信方式。
综上所述,错误装信数量方式数量为:

5. 母牛生产
题目描述:假设农场中成熟的母牛每年都会生 1 头小母牛,并且永远不会死。第一年有 1 只小母牛,从第二年开始,母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N,求 N 年后牛的数量。
第 i 年成熟的牛的数量为:

矩阵路径
1. 矩阵的最小路径和
64. Minimum Path Sum (Medium)
[[1,3,1],
[1,5,1],
[4,2,1]]
Given the above grid map, return 7. Because the path 1→3→1→1→1 minimizes the sum.
题目描述:求从矩阵的左上角到右下角的最小路径和,每次只能向右和向下移动。
//一维的比较难以理解,在先从上到下再从左到右的更新顺序中,当前行的dp[j]代表某一行的到达j列的路径,if (j == 0) dp[j] = dp[j]; 是承接上一行的路径记录的地方.
public int minPathSum(int[][] grid) {
if (grid.length == 0 || grid[0].length == 0) {
return 0;
}
int m = grid.length, n = grid[0].length;
int[] dp = new int[n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (j == 0) {
dp[j] = dp[j]; // 只能从上侧走到该位置
} else if (i == 0) {
dp[j] = dp[j - 1]; // 只能从左侧走到该位置
} else {
dp[j] = Math.min(dp[j - 1], dp[j]);
}
dp[j] += grid[i][j];
}
}
return dp[n - 1];
}
//我的
class Solution {
public int minPathSum(int[][] grid) {
int row = grid.length;
int col = grid[0].length;
int[][] dp = new int[row][col];
dp[0][0] = grid[0][0];
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(i==0 && j==0) continue;
// max_value 是因为不选这个更新方向的
dp[i][j] =grid[i][j] + Math.min(i == 0 ? Integer.MAX_VALUE : dp[i-1][j], j == 0 ? Integer.MAX_VALUE : dp[i][j-1]);
}
}
return dp[row -1][col - 1];
}
}
//可以在原数组上存储值,重点记忆
class Solution {
public int minPathSum(int[][] grid) {
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[0].length; j++) {
if(i == 0 && j == 0) continue;
else if(i == 0) grid[i][j] = grid[i][j - 1] + grid[i][j];
else if(j == 0) grid[i][j] = grid[i - 1][j] + grid[i][j];
else grid[i][j] = Math.min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
}
}
return grid[grid.length - 1][grid[0].length - 1];
}
}
2. 矩阵的总路径数
62. Unique Paths (Medium)
题目描述:统计从矩阵左上角到右下角的路径总数,每次只能向右或者向下移动。

思路一:排列组合
二维动规数组
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < n; i++) dp[0][i] = 1;
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
一维的
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
Arrays.fill(dp, 1);
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n - 1];
}
也可以直接用数学公式求解,这是一个组合问题。机器人总共移动的次数 S=m+n-2,向下移动的次数 D=m-1,那么问题可以看成从 S 中取出 D 个位置的组合数量,这个问题的解为 C(S, D)。
public int uniquePaths(int m, int n) {
int S = m + n - 2; // 总共的移动次数
int D = m - 1; // 向下的移动次数
long ret = 1;
for (int i = 1; i <= D; i++) {
ret = ret * (S - D + i) / i;
}
return (int) ret;
}
3.地下城
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
解答
1.因为生命值最小为1,所以降为0后人为置1
2.倒着循环,全循环,且增加下面一句以躲开目的地:
if (i == row - 1 && j == col - 1) {
continue;
}
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
int row = dungeon.length;
int col = dungeon[0].length;
int[][] dp = new int[row][col];
//dp表示想要到达某个地方至少需要的生命值,如果小于0,设置为1.
dp[row - 1][col - 1] = dungeon[row - 1][col - 1] > 0 ? 1 : -dungeon[row - 1][col - 1] + 1;
for (int i = row - 1; i >= 0; i--) {
for (int j = col - 1; j >= 0; j--) {
if (i == row - 1 && j == col - 1) {
continue;
}
int tep1 = i < row-1 ? dp[i + 1][j] - dungeon[i][j] : Integer.MAX_VALUE;
int tep2 = j < col-1 ? dp[i][j+1] - dungeon[i][j] : Integer.MAX_VALUE;
dp[i][j] = Math.min(tep1,tep2);
if(dp[i][j]<=0) dp[i][j] = 1;
}
}
return dp[0][0];
}
}
数组区间
1. 数组区间和
303. Range Sum Query - Immutable (Easy)
Given nums = [-2, 0, 3, -5, 2, -1]
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
求区间 i ~ j 的和,可以转换为 sum[j + 1] - sum[i],其中 sum[i] 为 0 ~ i - 1 的和。
class NumArray {
private int[] sums;
public NumArray(int[] nums) {
sums = new int[nums.length + 1];
for (int i = 1; i <= nums.length; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
}
public int sumRange(int i, int j) {
return sums[j + 1] - sums[i];
}
}
2. 数组中等差递增子区间的个数
413. Arithmetic Slices (Medium)
A = [0, 1, 2, 3, 4]
return: 6, for 3 arithmetic slices in A:
[0, 1, 2],
[1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3, 4],
[ 1, 2, 3, 4],
[2, 3, 4]
dp[i] 表示以 A[i] 为结尾的等差递增子区间的个数。
当 A[i] - A[i-1] == A[i-1] - A[i-2],那么 [A[i-2], A[i-1], A[i]] 构成一个等差递增子区间。而且在以 A[i-1] 为结尾的递增子区间的后面再加上一个 A[i],一样可以构成新的递增子区间。
dp[2] = 1
[0, 1, 2]
dp[3] = dp[2] + 1 = 2
[0, 1, 2, 3], // [0, 1, 2] 之后加一个 3
[1, 2, 3] // 新的递增子区间
dp[4] = dp[3] + 1 = 3
[0, 1, 2, 3, 4], // [0, 1, 2, 3] 之后加一个 4
[1, 2, 3, 4], // [1, 2, 3] 之后加一个 4
[2, 3, 4] // 新的递增子区间
综上,在 A[i] - A[i-1] == A[i-1] - A[i-2] 时,dp[i] = dp[i-1] + 1。
因为递增子区间不一定以最后一个元素为结尾,可以是任意一个元素结尾,因此需要返回 dp 数组累加的结果。
public int numberOfArithmeticSlices(int[] A) {
if (A == null || A.length == 0) {
return 0;
}
int n = A.length;
int[] dp = new int[n];
for (int i = 2; i < n; i++) {
if (A[i] - A[i - 1] == A[i - 1] - A[i - 2]) {
dp[i] = dp[i - 1] + 1;
}
}
int total = 0;
for (int cnt : dp) {
total += cnt;
}
return total;
}
轮询数组,满足情况是怎样,不满足就总结的方法,我叫做在线模拟法
//我的思路 ,轮询一遍,当
class Solution {
public int numberOfArithmeticSlices(int[] A) {
int res = 0;
int nums = 2;
for(int i = 2; i < A.length; i++){
if(A[i] - A[i-1] == A[i-1] - A[i-2]){
nums++;
}else{
if(nums > 2)
res += helper(nums);
nums = 2;
}
}
if(nums > 2)
res += helper(nums);
return res;
}
private static int helper(int nums){
int res = 0;
for(int i = 3; i <= nums; i++){
res += nums - i + 1;
}
return res;
}
}
分割整数
1. 分割整数的最大乘积
343. Integer Break (Medim)
//剪绳子问题
题目描述:For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i - 1; j++) {
dp[i] = Math.max(dp[i], Math.max(j * dp[i - j], j * (i - j)));
}
}
return dp[n];
}
2. 按平方数来分割整数
279. Perfect Squares(Medium)
也可以用bfs,在搜索部分中出现
题目描述:For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.
public int numSquares(int n) {
List<Integer> squareList = generateSquareList(n);
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = Integer.MAX_VALUE;
for (int square : squareList) {
if (square > i) {
break;
}
min = Math.min(min, dp[i - square] + 1);
}
dp[i] = min;
}
return dp[n];
}
private List<Integer> generateSquareList(int n) {
List<Integer> squareList = new ArrayList<>();
// n^2-(n-1)^2 = 2n - 1;所以每个n后diff加2
int diff = 3;
int square = 1;
while (square <= n) {
squareList.add(square);
square += diff;
diff += 2;
}
return squareList;
}
或者
class Solution {
public int numSquares(int n) {
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = Integer.MAX_VALUE;
for (int j = 1; j * j <= i; j++) {
//dp[i] = Math.min(dp[j] + dp[i - j], dp[i]);
dp[i] = Math.min(dp[i - j * j] + 1, dp[i]);
}
}
return dp[n];
}
}
3. 分割整数构成字母字符串
91. Decode Ways (Medium)
题目描述:Given encoded message “12”, it could be decoded as “AB” (1 2) or “L” (12).
public int numDecodings(String s) {
if (s == null || s.length() == 0) {
return 0;
}
int n = s.length();
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = s.charAt(0) == '0' ? 0 : 1;
for (int i = 2; i <= n; i++) {
int one = Integer.valueOf(s.substring(i - 1, i));
if (one != 0) {
dp[i] += dp[i - 1];
}
//不好处理等于0的问题
if (s.charAt(i - 2) == '0') {
continue;
}
int two = Integer.valueOf(s.substring(i - 2, i));
if (two <= 26) {
dp[i] += dp[i - 2];
}
}
return dp[n];
}
子序列
最长递增子序列
已知一个序列 {S1, S2,…,Sn},取出若干数组成新的序列 {Si1, Si2,…, Sim},其中 i1、i2 … im 保持递增,即新序列中各个数仍然保持原数列中的先后顺序,称新序列为原序列的一个 子序列 。
如果在子序列中,当下标 ix > iy 时,Six > Siy,称子序列为原序列的一个 递增子序列 。
定义一个数组 dp 存储最长递增子序列的长度,dp[n] 表示以 Sn 结尾的序列的最长递增子序列长度。对于一个递增子序列 {Si1, Si2,…,Sim},如果 im < n 并且 Sim < Sn,此时 {Si1, Si2,…, Sim, Sn} 为一个递增子序列,递增子序列的长度增加 1。满足上述条件的递增子序列中,长度最长的那个递增子序列就是要找的,在长度最长的递增子序列上加上 Sn 就构成了以 Sn 为结尾的最长递增子序列。因此 dp[n] = max{ dp[i]+1 | Si < Sn && i < n} 。
因为在求 dp[n] 时可能无法找到一个满足条件的递增子序列,此时 {Sn} 就构成了递增子序列,需要对前面的求解方程做修改,令 dp[n] 最小为 1,即:

对于一个长度为 N 的序列,最长递增子序列并不一定会以 SN 为结尾,因此 dp[N] 不是序列的最长递增子序列的长度,需要遍历 dp 数组找出最大值才是所要的结果,max{ dp[i] | 1 <= i <= N} 即为所求。
300. Longest Increasing Subsequence (Medium)
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
for (int i = 0; i < n; i++) {
int max = 1;
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
max = Math.max(max, dp[j] + 1);
}
}
dp[i] = max;
}
return Arrays.stream(dp).max().orElse(0);
}
使用 Stream 求最大值会导致运行时间过长,可以改成以下形式:
int ret = 0;
for (int i = 0; i < n; i++) {
ret = Math.max(ret, dp[i]);
}
return ret;
以上解法的时间复杂度为 O(N2),可以使用二分查找将时间复杂度降低为 O(NlogN)。
定义一个 tails 数组,其中 tails[i] 存储长度为 i + 1 的最长递增子序列的最后一个元素。对于一个元素 x,
- 如果它大于 tails 数组所有的值,那么把它添加到 tails 后面,表示最长递增子序列长度加 1;
- 如果 tails[i-1] < x <= tails[i],那么更新 tails[i] = x。
例如对于数组 [4,3,6,5],有:
tails len num
[] 0 4
[4] 1 3
[3] 1 6
[3,6] 2 5
[3,5] 2 null
可以看出 tails 数组保持有序,因此在查找 Si 位于 tails 数组的位置时就可以使用二分查找。
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] tails = new int[n];
int len = 0;
for (int num : nums) {
int index = binarySearch(tails, len, num);
tails[index] = num;
if (index == len) {
len++;
}
}
return len;
}
private int binarySearch(int[] tails, int len, int key) {
int l = 0, h = len;
while (l < h) {
int mid = l + (h - l) / 2;
if (tails[mid] == key) {
return mid;
} else if (tails[mid] > key) {
h = mid;
} else {
l = mid + 1;
}
}
return l;
}
2. 一组整数对能够构成的最长链
646. Maximum Length of Pair Chain (Medium)
Input: [[1,2], [2,3], [3,4]]
Output: 2
Explanation: The longest chain is [1,2] -> [3,4]
题目描述:对于 (a, b) 和 (c, d) ,如果 b < c,则它们可以构成一条链。
public int findLongestChain(int[][] pairs) {
if (pairs == null || pairs.length == 0) {
return 0;
}
Arrays.sort(pairs, (a, b) -> (a[0] - b[0]));
int n = pairs.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (pairs[j][1] < pairs[i][0]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
return Arrays.stream(dp).max().orElse(0);
}
3. 最长摆动子序列
376. Wiggle Subsequence (Medium)
Input: [1,7,4,9,2,5]
Output: 6
The entire sequence is a wiggle sequence.
Input: [1,17,5,10,13,15,10,5,16,8]
Output: 7
There are several subsequences that achieve this length. One is [1,17,10,13,10,16,8].
Input: [1,2,3,4,5,6,7,8,9]
Output: 2
要求:使用 O(N) 时间复杂度求解。
public int wiggleMaxLength(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int up = 1, down = 1;
for (int i = 1; i < nums.length; i++) {
if (nums[i] > nums[i - 1]) {
up = down + 1;
} else if (nums[i] < nums[i - 1]) {
down = up + 1;
}
}
return Math.max(up, down);
}
最长公共子序列
注意边界的处理:
-
数组初始为0,但是本题边界是1,所以就new一个边界加1的数组
-
单独拿出来处理
-
二层循环里判断
对于两个子序列 S1 和 S2,找出它们最长的公共子序列。
定义一个二维数组 dp 用来存储最长公共子序列的长度,其中 dp[i][j] 表示 S1 的前 i 个字符与 S2 的前 j 个字符最长公共子序列的长度。考虑 S1i 与 S2j 值是否相等,分为两种情况:
- 当 S1i==S2j 时,那么就能在 S1 的前 i-1 个字符与 S2 的前 j-1 个字符最长公共子序列的基础上再加上 S1i 这个值,最长公共子序列长度加 1,即 dp[i][j] = dp[i-1][j-1] + 1。
- 当 S1i != S2j 时,此时最长公共子序列为 S1 的前 i-1 个字符和 S2 的前 j 个字符最长公共子序列,或者 S1 的前 i 个字符和 S2 的前 j-1 个字符最长公共子序列,取它们的最大者,即 dp[i][j] = max{ dp[i-1][j], dp[i][j-1] }。
综上,最长公共子序列的状态转移方程为:

对于长度为 N 的序列 S1 和长度为 M 的序列 S2,dp[N][M] 就是序列 S1 和序列 S2 的最长公共子序列长度。
与最长递增子序列相比,最长公共子序列有以下不同点:
- 针对的是两个序列,求它们的最长公共子序列。
- 在最长递增子序列中,dp[i] 表示以 Si 为结尾的最长递增子序列长度,子序列必须包含 Si ;在最长公共子序列中,dp[i][j] 表示 S1 中前 i 个字符与 S2 中前 j 个字符的最长公共子序列长度,不一定包含 S1i 和 S2j。
- 在求最终解时,最长公共子序列中 dp[N][M] 就是最终解,而最长递增子序列中 dp[N] 不是最终解,因为以 SN 为结尾的最长递增子序列不一定是整个序列最长递增子序列,需要遍历一遍 dp 数组找到最大者。
public int lengthOfLCS(int[] nums1, int[] nums2) {
int n1 = nums1.length, n2 = nums2.length;
int[][] dp = new int[n1 + 1][n2 + 1];
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[n1][n2];
}
其他解法,注意边界的处理
class Solution {
public int findLength(int[] A, int[] B) {
int m = A.length;
int n = B.length;
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
if(A[i] == B[0]) dp[i][0] = 1;
}
for (int i = 0; i < n; i++) {
if(A[0] == B[i]) dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (A[i] == B[j]) dp[i][j] = dp[i-1][j-1] + 1;
}
}
return dp[m-1][n-1];
}
}
初始化的情况还可以简单一点,因为边缘确实默认为0,,有相等的为1,所以可以将单独考虑纳入到二层循环中去
class Solution {
public int findLength(int[] A, int[] B) {
int m = A.length;
int n = B.length;
int[][] dp = new int[m][n];
int max = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if(A[i] != B[j]){
continue;
}
dp[i][j] += 1;
if (i >0 && j > 0) dp[i][j] += dp[i-1][j-1];
max = Math.max(dp[i][j], max);
}
}
return max;
}
}
2.子序列的个数
1.字符串从0开始,dp[]中的数字是前多少个字符,所以if(s1.charAt(i - 1) == s2.charAt(j - 1))
2.技巧:二维dp中 一般长的作为一层循环
class Solution {
public int numDistinct(String s1, String s2) {
int m = s1.length(), n = s2.length();
int[][] f = new int[m + 1][n + 1];
for(int i = 0; i <= m; i++) f[i][0] = 1;
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
f[i][j] = f[i - 1][j];
if(s1.charAt(i - 1) == s2.charAt(j - 1)){
f[i][j] += f[i - 1][j - 1];
}
}
}
return f[m][n];
}
}
作者:a380922457
链接:https://leetcode-cn.com/problems/distinct-subsequences/solution/dong-tai-gui-hua-si-yao-su-by-a380922457-2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
乘积最大子序列
解题思路
这题是求数组中子区间的最大乘积,对于乘法,我们需要注意,负数乘以负数,会变成正数,所以解这题的时候我们需要维护两个变量,当前的最大值,以及最小值,最小值可能为负数,但没准下一步乘以一个负数,当前的最大值就变成最小值,而最小值则变成最大值了。
class Solution {
public int maxProduct(int[] nums) {
int prevMin = nums[0], prevMax = nums[0], res = nums[0];
int temp1 = 0, temp2 = 0;
for (int i = 1; i < nums.length; i++) {
temp1 = nums[i] * prevMax;
temp2 = nums[i] * prevMin;
prevMax = Math.max(Math.max(temp1, temp2), nums[i]);
prevMin = Math.min(Math.min(temp1, temp2), nums[i]);
res = Math.max(res, prevMax);
}
return res;
}
}
思路:乘积如果不考虑0的话肯定是两边开始最长的包含偶数个数负数的的最长子数组.
可以直接累乘
class Solution:
def maxProduct(self, nums: List[int]) -> int:
reverse_nums = nums[::-1]
for i in range(1, len(nums)):
nums[i] *= nums[i - 1] or 1
reverse_nums[i] *= reverse_nums[i - 1] or 1
return max(nums + reverse_nums)
最长上升子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
背包
有一个容量为 N 的背包,要用这个背包装下物品的价值最大,这些物品有两个属性:体积 w 和价值 v。
定义一个二维数组 dp 存储最大价值,其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。设第 i 件物品体积为 w,价值为 v,根据第 i 件物品是否添加到背包中,可以分两种情况讨论:
- 第 i 件物品没添加到背包,总体积不超过 j 的前 i 件物品的最大价值就是总体积不超过 j 的前 i-1 件物品的最大价值,
dp[i][j] = dp[i-1][j]。 - 第 i 件物品添加到背包中,
dp[i][j] = dp[i-1][j-w] + v。
第 i 件物品可添加也可以不添加,取决于哪种情况下最大价值更大。因此,0-1 背包的状态转移方程为:

// W 为背包总体积
// N 为物品数量
// weights 数组存储 N 个物品的重量
// values 数组存储 N 个物品的价值
public int knapsack(int W, int N, int[] weights, int[] values) {
int[][] dp = new int[N + 1][W + 1];
for (int i = 1; i <= N; i++) {
int w = weights[i - 1], v = values[i - 1];
for (int j = 1; j <= W; j++) {
if (j >= w) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w] + v);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[N][W];
}
空间优化
在程序实现时可以对 0-1 背包做优化。观察状态转移方程可以知道,前 i 件物品的状态仅与前 i-1 件物品的状态有关,因此可以将 dp 定义为一维数组,其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i][j]。此时,

因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w],防止将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
public int knapsack(int W, int N, int[] weights, int[] values) {
int[] dp = new int[W + 1];
for (int i = 1; i <= N; i++) {
int w = weights[i - 1], v = values[i - 1];
for (int j = W; j >= 1; j--) {
if (j >= w) {
dp[j] = Math.max(dp[j], dp[j - w] + v);
}
}
}
return dp[W];
}
无法使用贪心算法的解释
0-1 背包问题无法使用贪心算法来求解,也就是说不能按照先添加性价比最高的物品来达到最优,这是因为这种方式可能造成背包空间的浪费,从而无法达到最优。考虑下面的物品和一个容量为 5 的背包,如果先添加物品 0 再添加物品 1,那么只能存放的价值为 16,浪费了大小为 2 的空间。最优的方式是存放物品 1 和物品 2,价值为 22.
| id | w | v | v/w |
|---|---|---|---|
| 0 | 1 | 6 | 6 |
| 1 | 2 | 10 | 5 |
| 2 | 3 | 12 | 4 |
变种
-
完全背包:物品数量为无限个
-
多重背包:物品数量有限制
-
多维费用背包:物品不仅有重量,还有体积,同时考虑这两种限制
-
其它:物品之间相互约束或者依赖
1. 划分数组为和相等的两部分
416. Partition Equal Subset Sum (Medium)
Input: [1, 5, 11, 5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].
可以看成一个背包大小为 sum/2 的 0-1 背包问题。
public boolean canPartition(int[] nums) {
int sum = computeArraySum(nums);
if (sum % 2 != 0) {
return false;
}
int W = sum / 2;
boolean[] dp = new boolean[W + 1];
dp[0] = true;
for (int num : nums) { // 0-1 背包一个物品只能用一次
for (int i = W; i >= num; i--) { // 从后往前,先计算 dp[i] 再计算 dp[i-num]
dp[i] = dp[i] || dp[i - num];
}
}
return dp[W];
}
private int computeArraySum(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
return sum;
}
2. 改变一组数的正负号使得它们的和为一给定数
494. Target Sum (Medium)
Input: nums is [1, 1, 1, 1, 1], S is 3.
Output: 5
Explanation:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
There are 5 ways to assign symbols to make the sum of nums be target 3.
该问题可以转换为 Subset Sum 问题,从而使用 0-1 背包的方法来求解。
可以将这组数看成两部分,P 和 N,其中 P 使用正号,N 使用负号,有以下推导:
sum(P) - sum(N) = target
sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)
2 * sum(P) = target + sum(nums)
因此只要找到一个子集,令它们都取正号,并且和等于 (target + sum(nums))/2,就证明存在解。
public int findTargetSumWays(int[] nums, int S) {
int sum = computeArraySum(nums);
if (sum < S || (sum + S) % 2 == 1) {
return 0;
}
int W = (sum + S) / 2;
int[] dp = new int[W + 1];
dp[0] = 1;
for (int num : nums) {
for (int i = W; i >= num; i--) {
dp[i] = dp[i] + dp[i - num];
}
}
return dp[W];
}
private int computeArraySum(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
return sum;
}
DFS 解法:
public int findTargetSumWays(int[] nums, int S) {
return findTargetSumWays(nums, 0, S);
}
private int findTargetSumWays(int[] nums, int start, int S) {
if (start == nums.length) {
return S == 0 ? 1 : 0;
}
return findTargetSumWays(nums, start + 1, S + nums[start])
+ findTargetSumWays(nums, start + 1, S - nums[start]);
}
3. 01 字符构成最多的字符串
474. Ones and Zeroes (Medium)
Input: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
Output: 4
Explanation: There are totally 4 strings can be formed by the using of 5 0s and 3 1s, which are "10","0001","1","0"
这是一个多维费用的 0-1 背包问题,有两个背包大小,0 的数量和 1 的数量。
public int findMaxForm(String[] strs, int m, int n) {
if (strs == null || strs.length == 0) {
return 0;
}
int[][] dp = new int[m + 1][n + 1];
for (String s : strs) { // 每个字符串只能用一次
int ones = 0, zeros = 0;
for (char c : s.toCharArray()) {
if (c == '0') {
zeros++;
} else {
ones++;
}
}
for (int i = m; i >= zeros; i--) {
for (int j = n; j >= ones; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - zeros][j - ones] + 1);
}
}
}
return dp[m][n];
}
4. 找零钱的最少硬币数
322. Coin Change (Medium)
Example 1:
coins = [1, 2, 5], amount = 11
return 3 (11 = 5 + 5 + 1)
Example 2:
coins = [2], amount = 3
return -1.
题目描述:给一些面额的硬币,要求用这些硬币来组成给定面额的钱数,并且使得硬币数量最少。硬币可以重复使用。
- 物品:硬币
- 物品大小:面额
- 物品价值:数量
因为硬币可以重复使用,因此这是一个完全背包问题。完全背包只需要将 0-1 背包的逆序遍历 dp 数组改为正序遍历即可。
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
for (int coin : coins) {
for (int i = coin; i <= amount; i++) { //将逆序遍历改为正序遍历
if (i == coin) {
dp[i] = 1;
} else if (dp[i] == 0 && dp[i - coin] != 0) {
dp[i] = dp[i - coin] + 1;
} else if (dp[i - coin] != 0) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] == 0 ? -1 : dp[amount];
}
5. 找零钱的硬币数组合
518. Coin Change 2 (Medium)
Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
完全背包问题,使用 dp 记录可达成目标的组合数目。
public int change(int amount, int[] coins) {
if (coins == null) {
return 0;
}
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i - coin];
}
}
return dp[amount];
}
6. 字符串按单词列表分割
139. Word Break (Medium)
s = "leetcode",
dict = ["leet", "code"].
Return true because "leetcode" can be segmented as "leet code".
dict 中的单词没有使用次数的限制,因此这是一个完全背包问题。
该问题涉及到字典中单词的使用顺序,也就是说物品必须按一定顺序放入背包中,例如下面的 dict 就不够组成字符串 “leetcode”:
["lee", "tc", "cod"]
求解顺序的完全背包问题时,对物品的迭代应该放在最里层,对背包的迭代放在外层,只有这样才能让物品按一定顺序放入背包中。
public boolean wordBreak(String s, List<String> wordDict) {
int n = s.length();
boolean[] dp = new boolean[n + 1];
dp[0] = true;
for (int i = 1; i <= n; i++) {
for (String word : wordDict) { // 对物品的迭代应该放在最里层
int len = word.length();
if (len <= i && word.equals(s.substring(i - len, i))) {
dp[i] = dp[i] || dp[i - len];
}
}
}
return dp[n];
}
7. 组合总和
377. Combination Sum IV (Medium)
nums = [1, 2, 3]
target = 4
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
Therefore the output is 7.
涉及顺序的完全背包。
public int combinationSum4(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return 0;
}
int[] maximum = new int[target + 1];
maximum[0] = 1;
Arrays.sort(nums);
for (int i = 1; i <= target; i++) {
for (int j = 0; j < nums.length && nums[j] <= i; j++) {
maximum[i] += maximum[i - nums[j]];
}
}
return maximum[target];
}
股票交易
1. 需要冷却期的股票交易
309. Best Time to Buy and Sell Stock with Cooldown(Medium)
题目描述:交易之后需要有一天的冷却时间。
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0) {
return 0;
}
int N = prices.length;
int[] buy = new int[N];
int[] s1 = new int[N];
int[] sell = new int[N];
int[] s2 = new int[N];
s1[0] = buy[0] = -prices[0];
sell[0] = s2[0] = 0;
for (int i = 1; i < N; i++) {
buy[i] = s2[i - 1] - prices[i];
s1[i] = Math.max(buy[i - 1], s1[i - 1]);
sell[i] = Math.max(buy[i - 1], s1[i - 1]) + prices[i];
s2[i] = Math.max(s2[i - 1], sell[i - 1]);
}
return Math.max(sell[N - 1], s2[N - 1]);
}
2. 需要交易费用的股票交易
714. Best Time to Buy and Sell Stock with Transaction Fee (Medium)
Input: prices = [1, 3, 2, 8, 4, 9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:
Buying at prices[0] = 1
Selling at prices[3] = 8
Buying at prices[4] = 4
Selling at prices[5] = 9
The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
题目描述:每交易一次,都要支付一定的费用。

public int maxProfit(int[] prices, int fee) {
int N = prices.length;
int[] buy = new int[N];
int[] s1 = new int[N];
int[] sell = new int[N];
int[] s2 = new int[N];
s1[0] = buy[0] = -prices[0];
sell[0] = s2[0] = 0;
for (int i = 1; i < N; i++) {
buy[i] = Math.max(sell[i - 1], s2[i - 1]) - prices[i];
s1[i] = Math.max(buy[i - 1], s1[i - 1]);
sell[i] = Math.max(buy[i - 1], s1[i - 1]) - fee + prices[i];
s2[i] = Math.max(s2[i - 1], sell[i - 1]);
}
return Math.max(sell[N - 1], s2[N - 1]);
}
3.0 买卖股票的最佳时机
思路1:设置一个动态二位数组,ij表示买入和卖出的时机。有点小题大做了。
思路二:只需要一个值记录当前的历史最低值即可
class Solution {
public int maxProfit(int[] prices) {
int minP = Integer.MAX_VALUE;
int res = 0;
for(int i = 0; i < prices.length; i++){
minP = Math.min(minP, prices[i]);
res = Math.max(res, prices[i] - minP);
}
return res;
}
3.2买卖股票的最佳时机二
122. 买卖股票的最佳时机 II可以多次购买、
策略:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rClQnsTi-1593868309201)(C:\Users\sixin\AppData\Local\Temp\1589690496140.png)]
//贪心,只要在上涨时卖出即可,然后当时
class Solution {
public int maxProfit(int[] prices) {
int res = 0;
for(int i = 1; i < prices.length; i++){
if(prices[i] > prices[i-1]){
res+=prices[i]-prices[i-1];
}
}
return res;
}
}
3.3 买卖股票的最佳时机 III
只能进行两次的股票交易
123. Best Time to Buy and Sell Stock III (Hard)

public int maxProfit(int[] prices) {
int firstBuy = Integer.MIN_VALUE, firstSell = 0;
int secondBuy = Integer.MIN_VALUE, secondSell = 0;
for (int curPrice : prices) {
if (firstBuy < -curPrice) {
firstBuy = -curPrice;
}
if (firstSell < firstBuy + curPrice) {
firstSell = firstBuy + curPrice;
}
if (secondBuy < firstSell - curPrice) {
secondBuy = firstSell - curPrice;
}
if (secondSell < secondBuy + curPrice) {
secondSell = secondBuy + curPrice;
}
}
return secondSell;
}
class Solution {
public int maxProfit(int[] prices) {
if (prices.length == 0) {
return 0;
}
int s1 = -prices[0], s2 = Integer.MIN_VALUE,s3 = Integer.MIN_VALUE,s4 = Integer.MIN_VALUE;
for (int i = 1; i < prices.length; i++){
s1 = Math.max(s1, -prices[i]);
s2 = Math.max(s2, s1 + prices[i]);
s3 = Math.max(s3, s2 - prices[i]);
s4 = Math.max(s4, s3 + prices[i]);
}
return Math.max(s4, 0);
}
}
4. 只能进行 k 次的股票交易
188. Best Time to Buy and Sell Stock IV (Hard)
public int maxProfit(int k, int[] prices) {
int n = prices.length;
if (k >= n / 2) { // 这种情况下该问题退化为普通的股票交易问题
int maxProfit = 0;
for (int i = 1; i < n; i++) {
if (prices[i] > prices[i - 1]) {
maxProfit += prices[i] - prices[i - 1];
}
}
return maxProfit;
}
int[][] maxProfit = new int[k + 1][n];
for (int i = 1; i <= k; i++) {
int localMax = maxProfit[i - 1][0] - prices[0];
for (int j = 1; j < n; j++) {
maxProfit[i][j] = Math.max(maxProfit[i][j - 1], prices[j] + localMax);
localMax = Math.max(localMax, maxProfit[i - 1][j] - prices[j]);
}
}
return maxProfit[k][n - 1];
}
字符串
1. 删除两个字符串的字符使它们相等
583. Delete Operation for Two Strings (Medium)
Input: "sea", "eat"
Output: 2
Explanation: You need one step to make "sea" to "ea" and another step to make "eat" to "ea".
可以转换为求两个字符串的最长公共子序列问题。
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return m + n - 2 * dp[m][n];
}
2. 编辑距离
72. Edit Distance (Hard)
Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
Example 2:
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
题目描述:修改一个字符串成为另一个字符串,使得修改次数最少。一次修改操作包括:插入一个字符、删除一个字符、替换一个字符。
public int minDistance(String word1, String word2) {
if (word1 == null || word2 == null) {
return 0;
}
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
dp[i][0] = i;
}
for (int i = 1; i <= n; i++) {
dp[0][i] = i;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i][j - 1], dp[i - 1][j])) + 1;
}
}
}
return dp[m][n];
}
3. 复制粘贴字符
650. 2 Keys Keyboard (Medium)
题目描述:最开始只有一个字符 A,问需要多少次操作能够得到 n 个字符 A,每次操作可以复制当前所有的字符,或者粘贴。
Input: 3
Output: 3
Explanation:
Intitally, we have one character 'A'.
In step 1, we use Copy All operation.
In step 2, we use Paste operation to get 'AA'.
In step 3, we use Paste operation to get 'AAA'.
public int minSteps(int n) {
if (n == 1) return 0;
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) return i + minSteps(n / i);
}
return n;
}
public int minSteps(int n) {
int[] dp = new int[n + 1];
int h = (int) Math.sqrt(n);
for (int i = 2; i <= n; i++) {
dp[i] = i;
for (int j = 2; j <= h; j++) {
if (i % j == 0) {
dp[i] = dp[j] + dp[i / j];
break;
}
}
}
return dp[n];
}
字符串匹配
public static boolean isMatch(String s, String p) {
//如果s不为空,p为空,是匹配不成功的,直接返回false
if (s.length() != 0 && p.length() == 0)
return false;
int slen = s.length(), plen = p.length();
boolean[][] dp = new boolean[slen + 1][plen + 1];
dp[0][0] = true;
//边界条件的初始化
for (int j = 1; j <= plen && dp[0][j - 1]; j++)
dp[0][j] = p.charAt(j - 1) == '*';
for (int i = 1; i <= slen; i++) {
for (int j = 1; j <= plen; j++) {
char si = s.charAt(i - 1), pj = p.charAt(j - 1);
//下面是动态规划的状态转移方程
if (si == pj || pj == '?') {
dp[i][j] = dp[i - 1][j - 1];
} else if (pj == '*') {
dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
}
}
}
return dp[slen][plen];
}
作者:sdwwld
链接:https://leetcode-cn.com/problems/wildcard-matching/solution/javadong-tai-gui-hua-yi-ji-dai-ma-you-hua-by-sdwwl/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
正则表达式匹配
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ggODyCMd-1598623833858)(C:\Users\s50012937\AppData\Roaming\Typora\typora-user-images\image-20200706215820405.png)]
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
boolean[][] f = new boolean[m + 1][n + 1];
f[0][0] = true;
for (int i = 0; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p.charAt(j - 1) == '*') {
f[i][j] = f[i][j - 2];
if (matches(s, p, i, j - 1)) {
f[i][j] = f[i][j] || f[i - 1][j];
}
}
else {
if (matches(s, p, i, j)) {
f[i][j] = f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
public boolean matches(String s, String p, int i, int j) {
if (i == 0) {
return false;
}
if (p.charAt(j - 1) == '.') {
return true;
}
return s.charAt(i - 1) == p.charAt(j - 1);
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/regular-expression-matching/solution/zheng-ze-biao-da-shi-pi-pei-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
## 通配符匹配
[44. 通配符匹配](https://leetcode-cn.com/problems/wildcard-matching/)
```java
public static boolean isMatch(String s, String p) {
//如果s不为空,p为空,是匹配不成功的,直接返回false
if (s.length() != 0 && p.length() == 0)
return false;
int slen = s.length(), plen = p.length();
boolean[][] dp = new boolean[slen + 1][plen + 1];
dp[0][0] = true;
//边界条件的初始化
for (int j = 1; j <= plen && dp[0][j - 1]; j++)
dp[0][j] = p.charAt(j - 1) == '*';
for (int i = 1; i <= slen; i++) {
for (int j = 1; j <= plen; j++) {
char si = s.charAt(i - 1), pj = p.charAt(j - 1);
//下面是动态规划的状态转移方程
if (si == pj || pj == '?') {
dp[i][j] = dp[i - 1][j - 1];
} else if (pj == '*') {
dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
}
}
}
return dp[slen][plen];
}
作者:sdwwld
链接:https://leetcode-cn.com/problems/wildcard-matching/solution/javadong-tai-gui-hua-yi-ji-dai-ma-you-hua-by-sdwwl/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
正则表达式匹配
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Rblk3xnm-1595487867314)(C:\Users\s50012937\AppData\Roaming\Typora\typora-user-images\image-20200706215820405.png)]
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
boolean[][] f = new boolean[m + 1][n + 1];
f[0][0] = true;
for (int i = 0; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p.charAt(j - 1) == '*') {
f[i][j] = f[i][j - 2];
if (matches(s, p, i, j - 1)) {
f[i][j] = f[i][j] || f[i - 1][j];
}
}
else {
if (matches(s, p, i, j)) {
f[i][j] = f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
public boolean matches(String s, String p, int i, int j) {
if (i == 0) {
return false;
}
if (p.charAt(j - 1) == '.') {
return true;
}
return s.charAt(i - 1) == p.charAt(j - 1);
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/regular-expression-matching/solution/zheng-ze-biao-da-shi-pi-pei-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
最长回文子串
- 二维动规,对角值确定,求右上角的值
public class Solution {
public String longestPalindrome(String s) {
// 特判
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i, j] 是否是回文串
boolean[][] dp = new boolean[len][len];
char[] charArray = s.toCharArray();
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
for (int j = 1; j < len; j++) {
for (int i = 0; i < j; i++) {
if (charArray[i] != charArray[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][j] == true 成立,就表示子串 s[i..j] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
}
最长有效括号
https://leetcode-cn.com/problems/longest-valid-parentheses/
public class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
int dp[] = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] + ((i - dp[i - 1]) - 2 >= 0 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = Math.max(maxans, dp[i]);
}
}
return maxans;
}
}
二维
最大正方形
在一个由 0 和 1 组成的二维矩阵内,找到只包含 1 的最大正方形,并返回其面积。
示例:
输入:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
输出: 4
使用二维dp,dp[i][j]表示以此为右下角的最大的正方形的边长,然后从上向下循环一下,很自然的思路。
比较难想到的是递推公式,即第ij的元素是怎么通过左和上的元素求得。绿色的方块就是根据左和上的两个方块
public class n221 {
public int maximalSquare(char[][] matrix) {
//动态规划:
int maxLen = 0;
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return maxLen;
}
int row = matrix.length;
int col = matrix[0].length;
int[][] dp = new int[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (matrix[i][j] == '1'){
if(i == 0 || j == 0) dp[i][j] = 1;
else{
dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1])+1;
}
maxLen = Math.max(maxLen, dp[i][j]);
}
}
}
return maxLen * maxLen;
}
}
搜索问题
求某些特征的数
279. 完全平方数
错误的一种贪心思路:能用大数就用大数来减
非常想当然的一种想法:
如果是12
结果是3 1 1 1
然而正确的结果是4 4 4
(但是可以通过大部分的测试)
暴力递归,超时
class Solution {
public int numSquares(int n) {
int m = (new Double(Math.sqrt(n))).intValue();
if(m * m == n) return 1;
int res = n;
for (int i = 1; i <= m; i++) {
res = Math.min(numSquares(n - i * i) + 1, res);
}
return res;
}
}
之所以不行,是因为中间很多的计算都是重复的
动规
用下面的转移方程复杂度很高
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++)
dp[j] = max(dp[j], dp[j-i] + dp[i]);
}
正确的动规
class Solution {
public int numSquares(int n) {
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = Integer.MAX_VALUE;
for (int j = 1; j * j <= i; j++) {
dp[i] = Math.min(dp[i - j * j] + 1, dp[i]);
}
}
return dp[n];
}
}
# $$$$$$$$$$$$贪心
@[toc]
保证每次操作都是局部最优的,并且最后得到的结果是全局最优的。
## 1. 分配饼干
455\. Assign Cookies (Easy)
[Leetcode](https://leetcode.com/problems/assign-cookies/description/) / [力扣](https://leetcode-cn.com/problems/assign-cookies/description/)
```html
Input: grid[1,3], size[1,2,4]
Output: 2
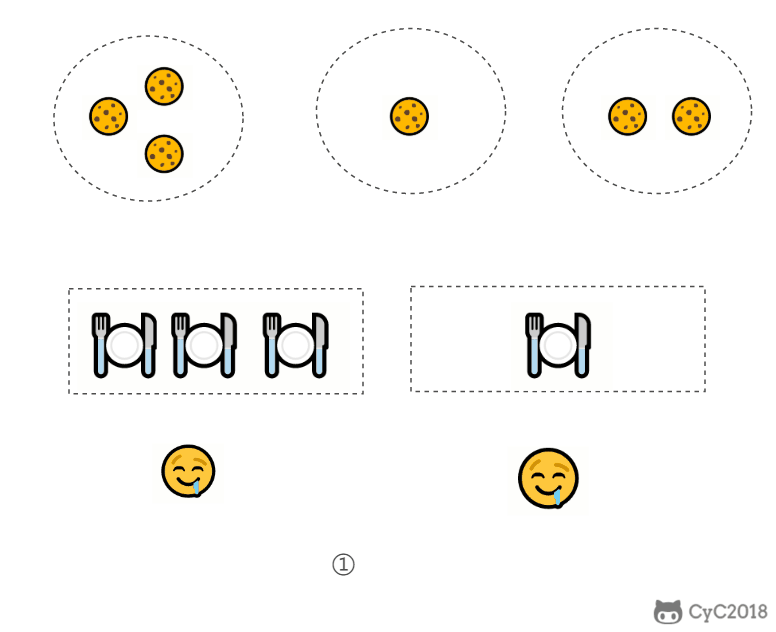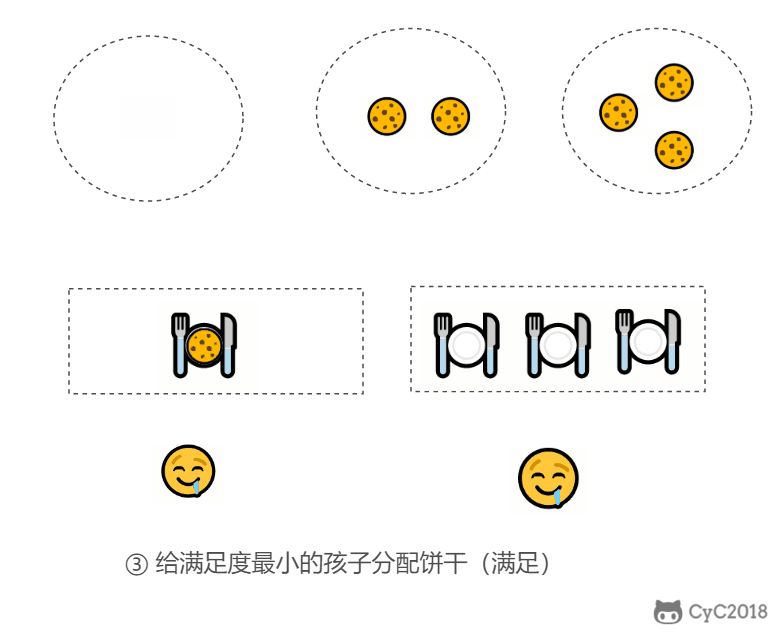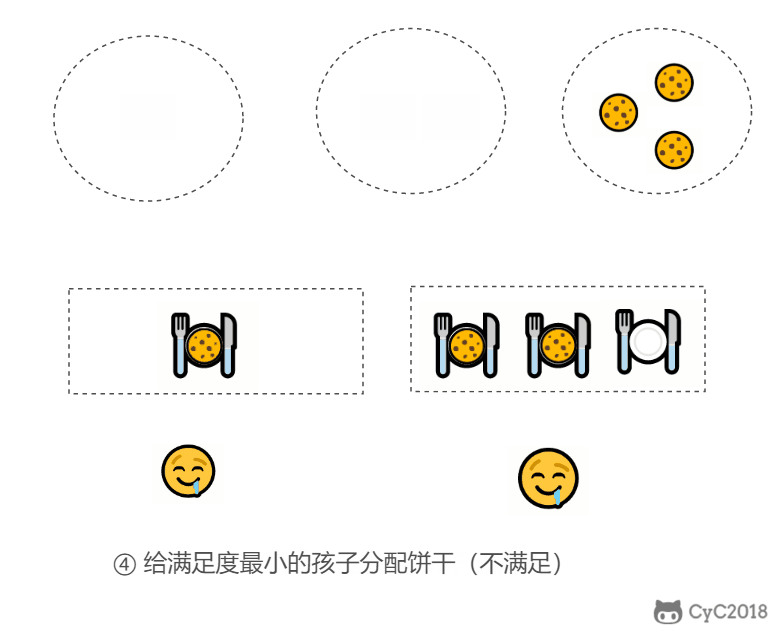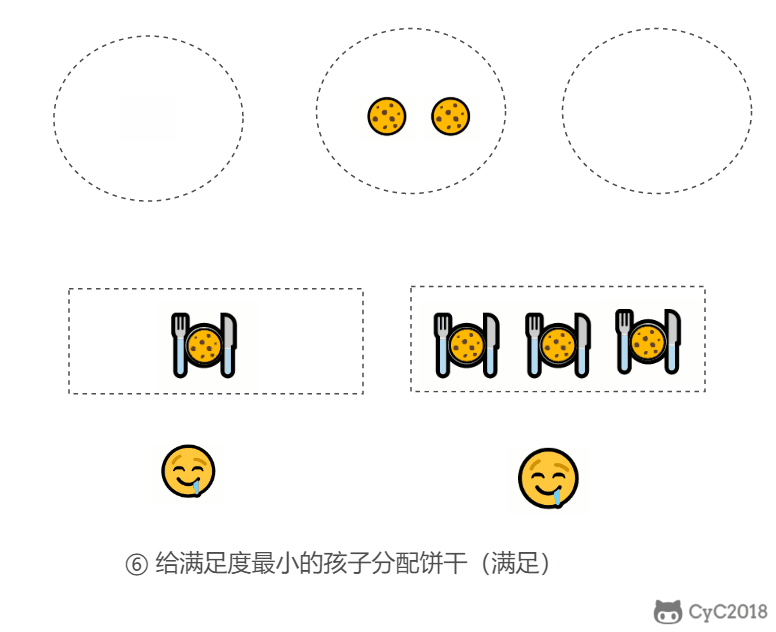
题目描述:每个孩子都有一个满足度 grid,每个饼干都有一个大小 size,只有饼干的大小大于等于一个孩子的满足度,该孩子才会获得满足。求解最多可以获得满足的孩子数量。
- 给一个孩子的饼干应当尽量小并且又能满足该孩子,这样大饼干才能拿来给满足度比较大的孩子。
- 因为满足度最小的孩子最容易得到满足,所以先满足满足度最小的孩子。
在以上的解法中,我们只在每次分配时饼干时选择一种看起来是当前最优的分配方法,但无法保证这种局部最优的分配方法最后能得到全局最优解。我们假设能得到全局最优解,并使用反证法进行证明,即假设存在一种比我们使用的贪心策略更优的最优策略。如果不存在这种最优策略,表示贪心策略就是最优策略,得到的解也就是全局最优解。
证明:假设在某次选择中,贪心策略选择给当前满足度最小的孩子分配第 m 个饼干,第 m 个饼干为可以满足该孩子的最小饼干。假设存在一种最优策略,可以给该孩子分配第 n 个饼干,并且 m < n。我们可以发现,经过这一轮分配,贪心策略分配后剩下的饼干一定有一个比最优策略来得大。因此在后续的分配中,贪心策略一定能满足更多的孩子。也就是说不存在比贪心策略更优的策略,即贪心策略就是最优策略。
public int findContentChildren(int[] grid, int[] size) {
if (grid == null || size == null) return 0;
Arrays.sort(grid);
Arrays.sort(size);
int gi = 0, si = 0;
while (gi < grid.length && si < size.length) {
if (grid[gi] <= size[si]) {
gi++;
}
si++;
}
return gi;
}
2. 不重叠的区间个数
435. Non-overlapping Intervals (Medium)
Input: [ [1,2], [1,2], [1,2] ]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.
Input: [ [1,2], [2,3] ]
Output: 0
Explanation: You don't need to remove any of the intervals since they're already non-overlapping.
题目描述:计算让一组区间不重叠所需要移除的区间个数。
先计算最多能组成的不重叠区间个数,然后用区间总个数减去不重叠区间的个数。
在每次选择中,区间的结尾最为重要,选择的区间结尾越小,留给后面的区间的空间越大,那么后面能够选择的区间个数也就越大。
按区间的结尾进行排序,每次选择结尾最小,并且和前一个区间不重叠的区间。
public int eraseOverlapIntervals(int[][] intervals) {
if (intervals.length == 0) {
return 0;
}
Arrays.sort(intervals, Comparator.comparingInt(o -> o[1]));
int cnt = 1;
int end = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] < end) {
continue;
}
end = intervals[i][1];
cnt++;
}
return intervals.length - cnt;
}
使用 lambda 表示式创建 Comparator 会导致算法运行时间过长,如果注重运行时间,可以修改为普通创建 Comparator 语句:
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
3. 投飞镖刺破气球
452. Minimum Number of Arrows to Burst Balloons (Medium)
Input:
[[10,16], [2,8], [1,6], [7,12]]
Output:
2
题目描述:气球在一个水平数轴上摆放,可以重叠,飞镖垂直投向坐标轴,使得路径上的气球都被刺破。求解最小的投飞镖次数使所有气球都被刺破。
也是计算不重叠的区间个数,不过和 Non-overlapping Intervals 的区别在于,[1, 2] 和 [2, 3] 在本题中算是重叠区间。
public int findMinArrowShots(int[][] points) {
if (points.length == 0) {
return 0;
}
Arrays.sort(points, Comparator.comparingInt(o -> o[1]));
int cnt = 1, end = points[0][1];
for (int i = 1; i < points.length; i++) {
if (points[i][0] <= end) {
continue;
}
cnt++;
end = points[i][1];
}
return cnt;
}
4. 根据身高和序号重组队列
406. Queue Reconstruction by Height(Medium)
Input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
题目描述:一个学生用两个分量 (h, k) 描述,h 表示身高,k 表示排在前面的有 k 个学生的身高比他高或者和他一样高。
为了使插入操作不影响后续的操作,身高较高的学生应该先做插入操作,否则身高较小的学生原先正确插入的第 k 个位置可能会变成第 k+1 个位置。
身高 h 降序、个数 k 值升序,然后将某个学生插入队列的第 k 个位置中。
public int[][] reconstructQueue(int[][] people) {
if (people == null || people.length == 0 || people[0].length == 0) {
return new int[0][0];
}
Arrays.sort(people, (a, b) -> (a[0] == b[0] ? a[1] - b[1] : b[0] - a[0]));
List<int[]> queue = new ArrayList<>();
for (int[] p : people) {
queue.add(p[1], p);
}
return queue.toArray(new int[queue.size()][]);
}
5. 买卖股票最大的收益
121. Best Time to Buy and Sell Stock (Easy)
题目描述:一次股票交易包含买入和卖出,只进行一次交易,求最大收益。
只要记录前面的最小价格,将这个最小价格作为买入价格,然后将当前的价格作为售出价格,查看当前收益是不是最大收益。
public int maxProfit(int[] prices) {
int n = prices.length;
if (n == 0) return 0;
int soFarMin = prices[0];
int max = 0;
for (int i = 1; i < n; i++) {
if (soFarMin > prices[i]) soFarMin = prices[i];
else max = Math.max(max, prices[i] - soFarMin);
}
return max;
}
6. 买卖股票的最大收益 II
122. Best Time to Buy and Sell Stock II (Easy)
题目描述:可以进行多次交易,多次交易之间不能交叉进行,可以进行多次交易。
对于 [a, b, c, d],如果有 a <= b <= c <= d ,那么最大收益为 d - a。而 d - a = (d - c) + (c - b) + (b - a) ,因此当访问到一个 prices[i] 且 prices[i] - prices[i-1] > 0,那么就把 prices[i] - prices[i-1] 添加到收益中。
public int maxProfit(int[] prices) {
int profit = 0;
for (int i = 1; i < prices.length; i++) {
if (prices[i] > prices[i - 1]) {
profit += (prices[i] - prices[i - 1]);
}
}
return profit;
}
7. 种植花朵
605. Can Place Flowers (Easy)
Input: flowerbed = [1,0,0,0,1], n = 1
Output: True
题目描述:flowerbed 数组中 1 表示已经种下了花朵。花朵之间至少需要一个单位的间隔,求解是否能种下 n 朵花。
public boolean canPlaceFlowers(int[] flowerbed, int n) {
int len = flowerbed.length;
int cnt = 0;
for (int i = 0; i < len && cnt < n; i++) {
if (flowerbed[i] == 1) {
continue;
}
int pre = i == 0 ? 0 : flowerbed[i - 1];
int next = i == len - 1 ? 0 : flowerbed[i + 1];
if (pre == 0 && next == 0) {
cnt++;
flowerbed[i] = 1;
}
}
return cnt >= n;
}
8. 判断是否为子序列
392. Is Subsequence (Medium)
s = "abc", t = "ahbgdc"
Return true.
public boolean isSubsequence(String s, String t) {
int index = -1;
for (char c : s.toCharArray()) {
index = t.indexOf(c, index + 1);
if (index == -1) {
return false;
}
}
return true;
}
9. 修改一个数成为非递减数组
665. Non-decreasing Array (Easy)
Input: [4,2,3]
Output: True
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.
题目描述:判断一个数组是否能只修改一个数就成为非递减数组。
在出现 nums[i] < nums[i - 1] 时,需要考虑的是应该修改数组的哪个数,使得本次修改能使 i 之前的数组成为非递减数组,并且 不影响后续的操作 。优先考虑令 nums[i - 1] = nums[i],因为如果修改 nums[i] = nums[i - 1] 的话,那么 nums[i] 这个数会变大,就有可能比 nums[i + 1] 大,从而影响了后续操作。还有一个比较特别的情况就是 nums[i] < nums[i - 2],修改 nums[i - 1] = nums[i] 不能使数组成为非递减数组,只能修改 nums[i] = nums[i - 1]。
public boolean checkPossibility(int[] nums) {
int cnt = 0;
for (int i = 1; i < nums.length && cnt < 2; i++) {
if (nums[i] >= nums[i - 1]) {
continue;
}
cnt++;
if (i - 2 >= 0 && nums[i - 2] > nums[i]) {
nums[i] = nums[i - 1];
} else {
nums[i - 1] = nums[i];
}
}
return cnt <= 1;
}
10. 子数组最大的和
53. Maximum Subarray (Easy)
For example, given the array [-2,1,-3,4,-1,2,1,-5,4],
the contiguous subarray [4,-1,2,1] has the largest sum = 6.
public int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int preSum = nums[0];
int maxSum = preSum;
for (int i = 1; i < nums.length; i++) {
preSum = preSum > 0 ? preSum + nums[i] : nums[i];
maxSum = Math.max(maxSum, preSum);
}
return maxSum;
}
11. 分隔字符串使同种字符出现在一起
763. Partition Labels (Medium)
Input: S = "ababcbacadefegdehijhklij"
Output: [9,7,8]
Explanation:
The partition is "ababcbaca", "defegde", "hijhklij".
This is a partition so that each letter appears in at most one part.
A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits S into less parts.
public List<Integer> partitionLabels(String S) {
int[] lastIndexsOfChar = new int[26];
for (int i = 0; i < S.length(); i++) {
lastIndexsOfChar[char2Index(S.charAt(i))] = i;
}
List<Integer> partitions = new ArrayList<>();
int firstIndex = 0;
while (firstIndex < S.length()) {
int lastIndex = firstIndex;
for (int i = firstIndex; i < S.length() && i <= lastIndex; i++) {
int index = lastIndexsOfChar[char2Index(S.charAt(i))];
if (index > lastIndex) {
lastIndex = index;
}
}
partitions.add(lastIndex - firstIndex + 1);
firstIndex = lastIndex + 1;
}
return partitions;
}
private int char2Index(char c) {
return c - 'a';
}
12.加油站
特点:只有一个,当前最大
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
//记录起始的位置
int start = 0;
//i是当前的位置
int totalTank = 0;
int curCost = 0;
//本题目的一个特点是肯定要计算所有的消耗的和的,所以用一个total来记录
for(int i = 0; i < gas.length; i++){
totalTank += gas[i]-cost[i];
curCost += gas[i]-cost[i];
if(curCost < 0){
start = i + 1;
curCost = 0;
}
}
return totalTank >= 0 ? start : -1;
}
}
13.分发糖果
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
左右扫描两遍
https://leetcode-cn.com/problems/candy/solution/fen-fa-tang-guo-by-powcai/
class Solution {
public int candy(int[] ratings) {
//思路:先使用一个基准的数字,1
int res = 0;
int[] dis = new int[ratings.length];
Arrays.fill(dis, 1);
for(int i = 1; i < ratings.length; i++){
if(ratings[i]>ratings[i-1]){
dis[i] = dis[i-1]+1;
}
}
res = dis[ratings.length-1];
for(int i = ratings.length - 2; i >= 0; i--){
if(ratings[i]>ratings[i+1]){
dis[i] = Math.max(dis[i+1]+1, dis[i]);
}
res += dis[i];
}
return res;
}
}
14.数位之积
现给定任意正整数 n,请寻找并输出最小的正整数 m(m>9),使得 m 的各位(个位、十位、百位 … …)之乘积等于n,若不存在则输出 -1。
public static int solution (int n) {
// write code here
int res = 0;
if(n <= 9) return 10+n;
int base = 1;
for(int i = 9; i > 0; i--){
//贪心算法尽量使高位的数字大,能除近的绝不移动
while(n % i == 0){
res += base*i;
//base 记录走到了多少位
base*=10;
n /= i;
}
}
return n==0 ? res : -1;
}





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








