1.复杂度和简单排序算法
- destination:一周刷爆LeetCode,算法大神左神(左程云)耗时100天打造算法与数据结构基础到高级全家桶教程,直击BTAJ等一线大厂必问算法面试题真题详解_哔哩哔哩_bilibili
- 1.复杂度
- 常数操作
- 常数操作:
- 加减乘除
- 位运算
- 查找数组第i个位置数据
- 非常数操作:
- 查找链表第i个位置的数据
- 常数操作:
- 时间复杂度:
- 定义:
- 时间复杂度的指标无法区分两个算法的优劣时,通过实际运行来确定
- 因为两个算法的常数操作都是固定时间,但是这两个固定时间可能会有所不同
- 定义:
- 常数操作
- 2.排序算法
- 选择排序
- 每一轮都要遍历剩余元素,找出其中最大(小)元素放在对应的位置
- 时间复杂度O(N^2),额外空间复杂度0(1)
- 冒泡排序
- 每一轮都要将剩余元素中相邻两两对比,判断是否交换两个元素的位置,该轮遍历之后最大(小)元素出现在对应的位置
- 时间复杂度O(N^2),额外空间复杂度0(1)
- 插入排序
- 从前向后,每一轮将待排序元素依次向前与已排序的元素比较判断是否需要交换,直到找到一个不再需要向前比较的位置,此时前面的元素相对有序
- 时间复杂度O(N^2),额外空间复杂度0(1)
- 选择排序数据状况不同,复杂度表现不一样
- 算法流程按照最差情况来估计时间复杂度

- 选择排序
- 3.异或运算
- a^b:相同为0,不同为1
- 异或运算也可以看成无进位相加(10110^10001=00111)
- 性质:
- 0^N=N N^N=0(实质是二进制补码的异或运算)
- 交换律:a^b=b^a
- 结合律:(a^b)^c=a^(b^c)
- 同一些数的异或结果是相同的,与计算顺序无关
- 应用(相当抖机灵,不要用):
- 交换函数:
- 前提:被交换值的两个数的地址不同

- 交换函数:
- 4.位运算的应用
- 1.整型数组中,时O(N),空O(1)
- 1)只有一种数出现了奇数次,其余数都出现了偶数次,找出这个数
- 初始整型变量eor=0,然后和所有数异或一遍,最后得到的结果就是出现奇数次的数
- 2)只有两种数出现了奇数次,其余数都出现了偶数次,找出这两个数
- 算法:
- 初始整型变量eor=0,然后和所有数异或一遍,最后得到的结果就是出现奇数次的数a和b异或的结果c
- 假设c第i位的数为1,则a和b在第i位的数第一个为1,另一个为0
- 初始整型变量eor1=0,然后异或所有第i位的数为1的数,得到结果为a
- b=a^c
- 代码:
- ~eor是eor取反,eor&(~eor+1)得到最右侧的1

- 算法:
- 1)只有一种数出现了奇数次,其余数都出现了偶数次,找出这个数
- 1.整型数组中,时O(N),空O(1)
- 5.二分法的详解与拓展
- 1)在一个有序数组中,找某个数是否存在
- 二分找中间值判断,找到这个数或找不到这个数
- 时间复杂度是判断次数,即O(log₂N),常写为O(logN)默认底数为2,其余底数要写明
- 2)在一个有序数组中,找>=某个数最左侧的位置
- 二分找中间值判断一直到结束,将最后二分得到的区域内数据全部判断一遍
- 3)局部最小值问题(无序也可以使用二分)
- 局部最小:对于相邻数不相等的无序数组,
- 如果0位置上的数小于1位置上的数,则0位置就是局部最小
- 如果N-1位置上的数小于N-2位置上的数,则N-1位置就是局部最小
- 如果中间位置i上的数既小于i-1位置上的数,也小于i+1位置上的数,则i位置就是局部最小
- 求一个局部最小的位置,能不能时间复杂度小于O(N)
- 先判断0位置和N-1位置是否是局部最小(若都不是,则之间必存在一个局部最小)
- 二分到死,肯定能找到一个局部最小
- 局部最小:对于相邻数不相等的无序数组,
- 1)在一个有序数组中,找某个数是否存在
- 6.对数器
- 对数器的概念和使用
- 1.有一个你想要测的方法a(比如自己想的)
- 2.实现复杂度不好但是容易实现的方法b(比如暴力解)
- 3.实现一个随机样本产生器
- 4.把方法a和方法b跑相同的随机样本,看看得到的结果是否一样
- 5.如果有一个随机样本使得比对结果不一致,打印样本进行人工干预,改对方法a或者方法b
- 6.当样本数量很多时比对测试依然正确,可以确定方法a已经正确
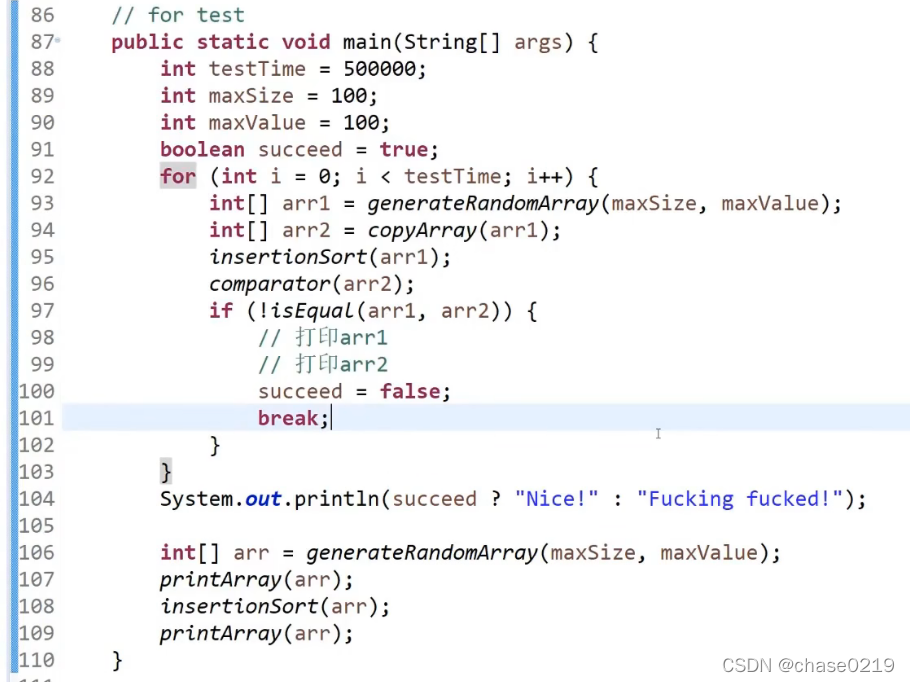
- 随机数组长度随机值,复制测试数据分别在两个方法里面跑,写一个isequal方法判断两个结果是否相同,测足够次数(几万几十万次)
- 对数器的概念和使用







 本文深入探讨了算法中的复杂度分析,重点讲解了选择排序、冒泡排序和插入排序的时间复杂度,并介绍了异或运算的性质和在交换函数中的应用。同时,阐述了位运算在整型数组处理中的高效策略,如找出出现奇数次的数。此外,还详细解析了二分法在有序数组查找中的多种应用场景。最后,提出了对数器的概念,用于验证算法复杂度的正确性。
本文深入探讨了算法中的复杂度分析,重点讲解了选择排序、冒泡排序和插入排序的时间复杂度,并介绍了异或运算的性质和在交换函数中的应用。同时,阐述了位运算在整型数组处理中的高效策略,如找出出现奇数次的数。此外,还详细解析了二分法在有序数组查找中的多种应用场景。最后,提出了对数器的概念,用于验证算法复杂度的正确性。

















 417
417

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








