学习simplified river plume算例
简介
本算例模拟了一个理想海岸的河流羽流运动。在一个理想的矩形计算域内,我们放入一定深度的盐水;我们再在一个边界的某一处添加一个入流边界条件,以输入淡水,并以此模拟河流的输入。在模拟结果中,我们能看到一个简单的羽流形成过程,及羽流的各个结构。
此外,该算例也能让大家熟悉边界条件的配置。该算例的文件位于 /examples/boundaries 文件夹中。
网格配置
本例采用一个三维网格。从水平面上看,计算域为一个场3km,宽1km的矩形,其网格均为三角形。从垂向看,网格被均分为了10层(suntans.dat: Nkmax=10, rstretch=1)。网格配置如下图所示。

定解条件设置
初始条件设置
在本算例中,需要设定的初始条件为水深和初始盐度。相关设置都在 initialization.c 文件中。
初始水深和初始水位分别通过函数 ReturnDepth 和 ReturnFreeSurface 设定:
REAL ReturnDepth(REAL x, REAL y) {
REAL length, xmid, shelfdepth, depth;
return 10;
}
REAL ReturnFreeSurface(REAL x, REAL y, REAL d) {
return 0;
}
初始盐度场通过函数 ReturnSalinity 设定:
REAL ReturnSalinity(REAL x, REAL y, REAL z) {
return 0;
}
即初始盐度场标记为0(这个0并不是实际意义上的0密度,而是表面初始场密度为参考密度)。
边界条件设置
在本算例中,需要设定的边界条件有两部分,第一是南侧(y=0)的入流边界,另一个是东侧的流出边界(开边界的一种)。如下图所示,描粗的边即计算域中需要设定边界条件的边。相关设置都在 initialization.c 文件中。

开边界处的通量计算(OpenBoundaryFluxes)
void OpenBoundaryFluxes(REAL **q, REAL **ub, REAL **ubn, gridT *grid, physT *phys, propT *prop) {
int j, jptr, ib, k, forced;
REAL *uboundary = phys->a, **u = phys->uc, **v = phys->vc, **uold = phys->uold, **vold = phys->vold;
REAL z, c0, c1, C0, C1, dt=prop->dt, u0, u0new, uc0, vc0, uc0old, vc0old, ub0;
for(jptr=grid->edgedist[2];jptr<grid->edgedist[3];jptr++) {
j = grid->edgep[jptr];
ib = grid->grad[2*j];
for(k=grid->etop[j];k<grid->Nke[j];k++)
ub[j][k]=0;
if(grid->yv[ib]>50) {
for(k=grid->etop[j];k<grid->Nke[j];k++)
ub[j][k]=-phys->h[ib]*sqrt(prop->grav/grid->dv[ib]);
} else {
if(grid->xv[ib]>900&&grid->xv[ib]<1200)
for(k=grid->etop[j];k<grid->Nke[j];k++)
ub[j][k]=phys->boundary_u[jptr-grid->edgedist[2]][k]*grid->n1[j]+
phys->boundary_v[jptr-grid->edgedist[2]][k]*grid->n2[j];
}
}
}
上述代码表达了这样的含义,在edge mark = 2的边中( for(jptr=grid->edgedist[2];jptredgedist[3];jptr++) ),我们首先找到中心点坐标 yv>50 的边,即东边界。并计算东边界的通量为:
ub[j][k]=-phys->h[ib]*sqrt(prop->grav/grid->dv[ib]);
这对应了如下数学表达式:
u
b
=
−
h
b
g
d
u_b=-h_b \sqrt{ \frac {g} {d}}
ub=−hbdg
式子中,hb表示边界处的水位,g是重力加速度,d是边界处对应的水深。这个式子表示了一种开边界,即水流可以自由地流出东边界。
而对于edge mark = 2的边中 yv<50 的南边界,则我们需要在 900m<xv<1200m 的网格上施加一个入流通量,这个通量根据边界速度计算:
ub[j][k]=phys->boundary_u[jptr-grid->edgedist[2]][k]*grid->n1[j]+
phys->boundary_v[jptr-grid->edgedist[2]][k]*grid->n2[j];
这个代码式的含义即将笛卡尔坐标系下的boundary_u和boundary_v,通过投影的方式计算得到网格边界的通量;也即:
u
b
=
(
b
o
u
n
d
a
r
y
u
,
b
o
u
n
d
a
r
y
v
)
⋅
n
⃗
=
(
b
o
u
n
d
a
r
y
u
,
b
o
u
n
d
a
r
y
v
)
⋅
(
n
1
,
n
2
)
u_b = (boundary_u, boundary_v) \cdot \vec{n} = (boundary_u, boundary_v) \cdot (n_1,n_2)
ub=(boundaryu,boundaryv)⋅n=(boundaryu,boundaryv)⋅(n1,n2)
式子中,向量n表示网格边界的法向量。
开边界处的速度、水位(BoundaryVelocities和SetUVWH)
void BoundaryVelocities(gridT *grid, physT *phys, propT *prop, int myproc, MPI_Comm comm) {
int jptr, j, ib, k;
REAL z;
for(jptr=grid->edgedist[2];jptr<grid->edgedist[3];jptr++) {
j = grid->edgep[jptr];
ib = grid->grad[2*j];
for(k=grid->etop[j];k<grid->Nke[j];k++) {
phys->boundary_u[jptr-grid->edgedist[2]][k]=0;
phys->boundary_v[jptr-grid->edgedist[2]][k]=0;
phys->boundary_w[jptr-grid->edgedist[2]][k]=0;
}
if(grid->yv[ib]>50) {
for(k=grid->etop[j];k<grid->Nke[j];k++) {
phys->boundary_u[jptr-grid->edgedist[2]][k]=phys->uc[ib][k];
phys->boundary_v[jptr-grid->edgedist[2]][k]=phys->vc[ib][k];
phys->boundary_w[jptr-grid->edgedist[2]][k]=0.5*(phys->w[ib][k]+phys->w[ib][k+1]);
}
} else {
if(grid->xv[ib]>900 && grid->xv[ib]<1200) {
z=0;
for(k=grid->etop[j];k<grid->Nke[j];k++) {
z-=0.5*grid->dzz[ib][k];
if(z>-3.0)
phys->boundary_v[jptr-grid->edgedist[2]][k]=prop->amp;
z-=0.5*grid->dzz[ib][k];
}
}
}
}
}
注:ib表示边界相邻网格的索引。
在BoundaryVelocities中,我们首先也要找到通过 edge mark = 2 和 yv>50 找到东边界,然后将boundary_u、boundary_v和boundary_w均设置为边界相邻网格的速度。这里要注意的是,由于在网格中,垂向速度w定义在垂向网格界面上,所以boundary_w通过取相邻网格的值做平均来得到。
而对于南边界,该算例将高程 -3.0 (水深小于3m)的 900m<xv<1200m 网格设置为了入流网格,即入流网格并未延伸至计算域的底部,而是在水面至水深3.0的部分。对于入流边界,我们设置boundary_v = amp。在本例中,amp在suntans.dat中设定,amp= 0.005 (单位m/s)。
static void SetUVWH(gridT *grid, physT *phys, propT *prop, int ib, int j, int boundary_index, REAL boundary_flag) {
int k;
if(boundary_flag==open) {
phys->boundary_h[boundary_index]=phys->h[ib];
for(k=grid->ctop[ib];k<grid->Nk[ib];k++) {
phys->boundary_u[boundary_index][k]=phys->uc[ib][k];
phys->boundary_v[boundary_index][k]=phys->vc[ib][k];
phys->boundary_w[boundary_index][k]=0.5*(phys->w[ib][k]+phys->w[ib][k+1]);
}
} else {
phys->boundary_h[boundary_index]=prop->amp*fabs(cos(prop->omega*prop->rtime));
for(k=grid->ctop[ib];k<grid->Nk[ib];k++) {
phys->boundary_u[boundary_index][k]=phys->u[j][k]*grid->n1[j];
phys->boundary_v[boundary_index][k]=phys->u[j][k]*grid->n2[j];
phys->boundary_w[boundary_index][k]=0.5*(phys->w[ib][k]+phys->w[ib][k+1]);
}
}
}
同理,SetUVWH中确定了边界速度,还确定了边界处的水位boundary_h。对于开边界,boundary_h 亦采用了相邻网格的h,即phys->h[ib]。
开边界处的盐度(BoundaryScalars)
void BoundaryScalars(gridT *grid, physT *phys, propT *prop, int myproc, MPI_Comm comm) {
int jptr, j, ib, k;
REAL z;
for(jptr=grid->edgedist[2];jptr<grid->edgedist[3];jptr++) {
j=grid->edgep[jptr];
ib=grid->grad[2*j];
for(k=grid->ctop[ib];k<grid->Nk[ib];k++) {
phys->boundary_T[jptr-grid->edgedist[2]][k]=phys->T[ib][k];
phys->boundary_s[jptr-grid->edgedist[2]][k]=phys->s[ib][k];
}
z=0;
if(grid->yv[ib]<50)
if(grid->xv[ib]>900 && grid->xv[ib]<1200)
for(k=grid->ctop[ib];k<grid->Nk[ib];k++) {
z-=0.5*grid->dzz[ib][k];
if(z>-3.0) {
phys->boundary_T[jptr-grid->edgedist[2]][k]=phys->T[ib][k];
phys->boundary_s[jptr-grid->edgedist[2]][k]=-0.0001;
} else {
phys->boundary_T[jptr-grid->edgedist[2]][k]=phys->T[ib][k];
phys->boundary_s[jptr-grid->edgedist[2]][k]=0;
}
z-=0.5*grid->dzz[ib][k];
}
}
}
第一部分的代码块表示:对于除了入流边界外的开边界,boundary_T和boundary_S分别设置为相邻网格的温度值与盐度值,即均采用温度和盐度的零梯度边界条件(注:在本例中,温度不影响水的密度)。对于入流边界,我们设定温度的边界值boundary_T为相邻网格的温度值,即采用零温度梯度的边界条件;而将入流的盐度条件将采用如下方式设定:
ρ
i
n
f
l
o
w
=
{
Δ
ρ
if
z
>
−
3.0
0
if
o
t
h
e
r
w
i
s
e
\rho _{inflow}=\begin{cases} \Delta \rho &\text{if } z>-3.0 \\ 0 &\text{if }otherwise \end{cases}
ρinflow={Δρ0if z>−3.0if otherwise
密度状态方程
在本算例中,水体密度仅由盐度s确定,其状态方程表达式体现在 state.c 文件的 StateEquation 函数中:
REAL StateEquation(const propT *prop, const REAL s, const REAL T, const REAL p) {
return prop->beta*s;
}
其中,beta为定值参数,在 /rundata/suntans.dat 中指定。在此例中,beta = 1.0。
其它参数配置
该算例采用非静压模拟(suntans.dat: nonhydrostatic = 1),时间步长为Δt=60s (suntans.dat: dt = 60),总共运行3000个时间步(suntans.dat: nstep = 3000),并每隔120步输出一次结果(suntans.dat: ntout = 120)。水体的分子粘度采用1e-4 m2/s,盐度的水平、垂向扩散系数均设置为0。动量平流项采用中心差分格式(suntans.dat: nonlinear = 2),并采用2.5阶Mellor-Yamada紊流模型(suntans.dat: turbmodel = 1)。
此外,模拟考虑了科氏力效应,设置科氏力系数Coriolis_f = 5e-4。
模拟结果
首先展示羽流形态的发展过程,其中云图颜色表示参考盐度的大小,箭头表示速度矢量。
- t = 10 hrs
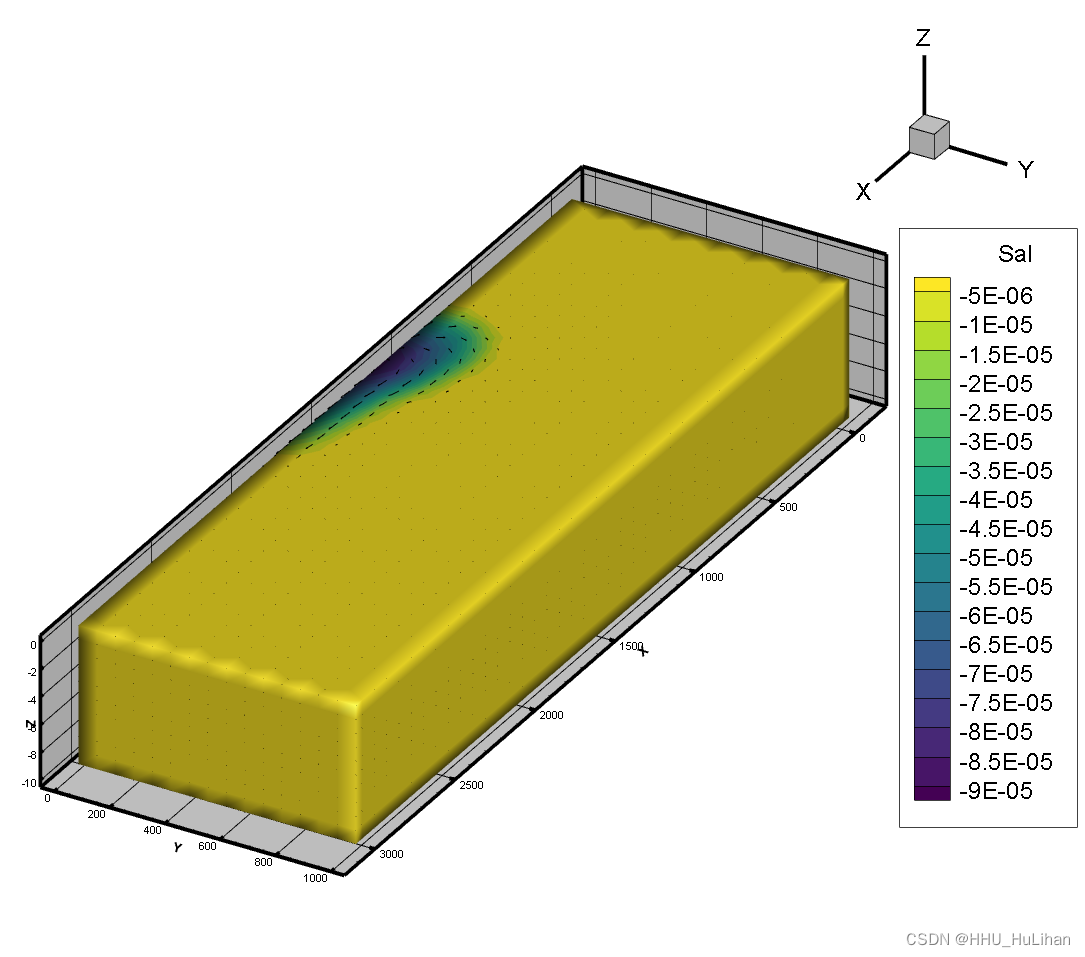
- t = 20 hrs

- t = 30 hrs

- t = 40 hrs

- t = 50 hrs

此外,水位结果也清晰表面了近场羽流的凸起结构(Bulge),及沿岸流结构。
以下展示 t = 50 hrs 时刻水位的平面分布。












 本文介绍了一个简化河流羽流运动的数值模拟案例。该案例通过在理想海岸线上建立三维网格,模拟淡水流入盐水环境中形成的羽流现象。文章详细介绍了网格配置、初始条件设置、边界条件配置等关键步骤。
本文介绍了一个简化河流羽流运动的数值模拟案例。该案例通过在理想海岸线上建立三维网格,模拟淡水流入盐水环境中形成的羽流现象。文章详细介绍了网格配置、初始条件设置、边界条件配置等关键步骤。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








