非静压模型NHWAVE学习（3）——考虑斜压问题的控制方程、控制方程的通量形式

考虑斜压问题的控制方程

在非静压模型NHWAVE学习（1）中，我们学习了模型的控制方程（如下图所示）。但实际上，由于NHWAVE模型的版本不断地更新迭代，计算模块不断增加（例如植被、泥沙输运等），现在的模型源代码所遵循的方程实际上远比下图所示的要复杂；简单来说，现版本NHWAVE中，控制方程中含有更多、更为复杂的项。

在这篇blog中，我们着重介绍NHWAVE的开发组学者Gangfeng Ma所引入的斜压项¹；他的这项工作使得NHWAVE可以模拟由于密度差异而引起的斜压问题，从而使模型的应用范围扩展到盐度、泥沙等物质输运过程的数值模拟中。
何为斜压（Baroclinic）问题？我们首先要知道，斜压这个概念是相对于正压（Barotropic）而言的。在流体力学中，若等压面和等密度面相重合，则根据状态方程知，此时的密度仅收到液体压强的控制；但在实际的河口、海洋或是湖泊、水库中，水体温度、盐度、泥沙含量等也会显著地影响流体的密度，而此时的流体等压面不再与等密度面相互交割，故称“斜压”。

斜压项

简单来说，只要我们考虑盐度、泥沙、温度等对水体密度的影响时，我们需要进行斜压问题的模拟。在NHWAVE模型中，Ma在动量方程中添加了一个密度项（或称斜压力项，如下图红圈所示）：

斜压项在σ坐标下的形式

于是，动量方程经σ坐标系转化后，将变为如下的形式

此处的S为方程的源项。



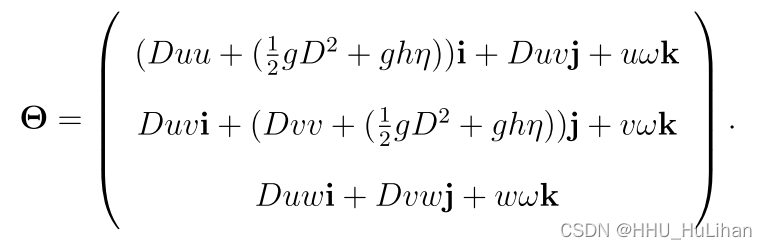
此时，注意这个源项，它可以被表达为

其中，S_h,S_p,S_ρ和S_τ分别表示了底部摩阻力项、动压力梯度项目、斜压项和扩散项，它们的表达式为，

其中，

ρ₀为清水的密度。详细可见NHWAVE模型手册及Gangfeng Ma等人的论文¹。
经过上述的处理，NHWAVE模型可以考虑斜压作用之影响。

控制方程（动量方程）的通量形式

NHWAVE主要是通过有限体积法进行空间离散的。为了便于有限体积法的实施，模型源代码中对控制方程的计算一般采用其通量形式。我们进行动量方程的转化，将

转化为如下形式，


其中，源项S_p,S_ρ和S_τ的形式在上一小节中给出；为了保持静水状态下，压力项与底摩阻项的平衡性，S_h将被改写成如下形式

参考文献

---

1. Ma G , Kirby J T , F Shi. Numerical simulation of tsunami waves generated by deformable submarine landslides[J]. Ocean Modelling, 2013, 69(Complete):146-165. ↩︎ ↩︎