【读书2】【2014】基于MATLAB的雷达信号处理基础（第二版）——分布式目标的距离方程(5)

在面散射中，微分RCS与散射面微分面积成正比，可以表示为

In area scattering the differential RCS isproportional to the differential area of the scattering surface and can berepresented as

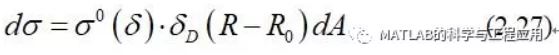
其中σ0（读作“西格玛零”）为面反射率，单位m2/m2，因此无量纲。

where σ0 (called “sigmanought”) is the area reflectivity in m2/m2 and istherefore dimensionless.

许多表面类型的面反射率都是掠射角δ的重要函数。

The area reflectivity of many surface typesis a significant function of the grazing angle δ.

通用的雷达距离方程（式2.17）修改为

The generalized range equation [Eq. (2.17)]becomes

其中ΔA为距离R0处的照射面积。

where ΔA is the illuminated area at range R0.

如果被照射区域受到波束的限制，将图2.3a的几何关系应用于距离R0上的微分散射单元，则在某时刻对后向散射起作用的区域为R2ϕ3θ3/sinδ。

If the illuminated area is beam limited,applying the geometry of Fig. 2.3ato the differential scattering element at range R0 shows that thearea contributing to the backscatter at one instant is R2ϕ3θ3/sinδ.

因此，微分面积对接收回波功率的贡献为

Thus, adifferential area contributing to the received power is of the form

将上式代入（2.28），同时假设天线的3-dB波束宽度范围内近似为恒定增益：

Applying this to Eq. (2.28) and again usingthe constant-gain approximation to the antenna 3-dB beamwidth gives thebeam-limited range equation for area scatterers:

如果被照射区域受到脉冲限制，图2.3b的几何关系表明，在某时刻对后向散射起作用的区域为Rθ3ΔR/cosδ。

If the illuminated area is pulse limited,the geometry of Fig. 2.3b shows that the area contributing to the backscatterat one instant is Rθ3ΔR/cosδ.

则

可以再次使用主瓣上的一阶恒定增益近似值，尽管现在ϕ上的积分限制在覆盖地面脉冲照射的范围内。

The first-order approximation of constantgain over the mainlobe can be used again, though the integral over ϕ is nowlimited to the range that covers the extent of the pulse on the ground.

则式（2.28）可改写为

Equation (2.28) becomes

请注意，在波束限制的情况下，接收功率随R-2变化，这与体散射一样，分辨率单元的大小在横向距离和下视范围内都随着距离的增大而增大。

Note that power varies as R-2 in the beam-limited casebecause, as with the volume scattering, the resolution cell size grows in bothcross-range and downrange extent with increasing range.

在脉冲限制的情况下，功率随R-3变化，因为分辨率单元仅在横向距离范围内随距离的增大而增大。

In the pulse-limited case, power varies asR-3 because the resolution cell extent increases in only thecross-range dimension with increasing range.

如果感兴趣的范围变化很大，掠射角δ就会有很大的变化，因此天线波束和脉冲脚印范围都会有很大的变化。

If the range of interest varies by a largeamount, there will be significant variation in the grazing angle δ andtherefore in both the antenna beam and pulse footprint extents.

例如，对于恒定高度h、斜距R的雷达，有sinδ = h/R。

For instance, for a radar at a constantaltitude h and a slant range R to the ground, sinδ = h/R.

随着R的增大，几何关系由“波束限制”变化为“脉冲限制”。

As R increases, the beam-limited antennafootprint area will then increase as R3 instead of R2 sothat the clutter power would be expected to fall only as R-1 .

然而，σ0也可能随掠射角而显著变化（见第2.3.1节）。

However, σ0 may also varysignificantly with grazing angle (see Section 2.3.1).

当距离R增大到一定程度时，会出现更复杂的情况，即波束限制出现在相对较近的距离和陡峭的掠射角时，脉冲限制出现在较远的距离和较浅的掠射角时，或者掠射角低于“临界角”。

Additional complications occur when R increasesso much that a radar that was beam limited at a relatively short range andsteep grazing angle becomes pulse limited at a longer range and shallowergrazing angle, or the grazing angle falls below the “critical angle”.

因此，接收到的杂波功率可能会以不同的速率从R-1下降到R-3，甚至在非常小的掠射角度时下降得更快(Long, 2001; Currie, 2010)。

Consequently, the received clutter powermay fall off at various rates from R-1to R-3 or evenmore rapidly at very shallow angles (Long, 2001; Currie, 2010).

——本文译自Mark A. Richards所著的《Fundamentals of Radar Signal Processing（Second edition）》

更多精彩文章请关注微信号：