概率分布实践

基本概念

PDF：概率密度函数（probability density function），连续型随机变量的概率密度函数

PMF : 概率质量函数（probability mass function)，离散随机变量在各特定取值上的概率。

CDF : 累积分布函数 (cumulative distribution function)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。
PPF ：CDF的逆

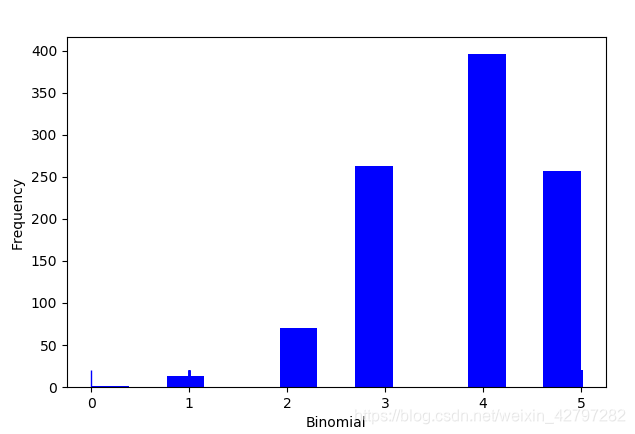
二项分布

data_binom = binom.rvs(n=5,p=0.75, size=1000)
ax = sn.distplot(data_binom,
                 hist=False,
                  kde=True,rug=True,
                  color='blue',
                  hist_kws={"linewidth":80,'alpha':1}
                    )
ax.set(xlabel='Binomial', ylabel='Frequency')
plt.show()

正态分布

loc = 1#均值
scale = 2.0#标准差
x = np.linspace(norm.ppf(0.01, loc, scale), norm.ppf(0.99, loc, scale), 100)
plt.plot(x, norm.pdf(x, loc, scale), 'b-', label='norm')
plt.title(u'正太分布概率密度函数')
plt.show()

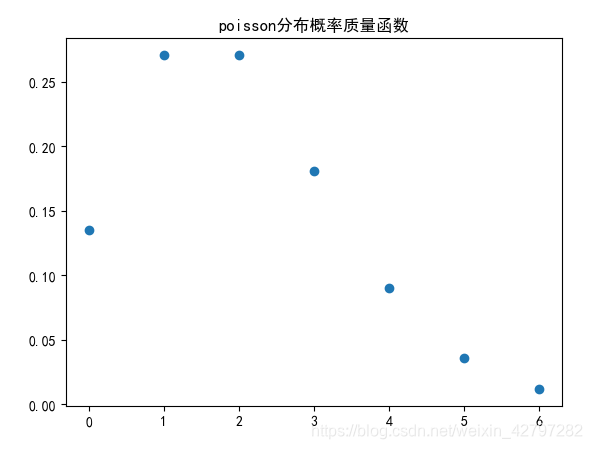
泊松分布

mu = 2 #λ 平均一段时间内发生了几次事件
x = np.arange(poisson.ppf(0.01, mu),poisson.ppf(0.99, mu)+1)
plt.plot(x, poisson.pmf(x, mu),'o')
plt.title(u'poisson分布概率质量函数')
plt.show()

伯努利分布

在这里插入代data_binom = binom.rvs(n=1,p=0.75, size=1000)
ax = sn.distplot(data_binom,
                 hist=True,
                  kde=False,rug=True,#核密度y轴表示概率密度函数是累计概率！！
                  color='blue',
                  hist_kws={"linewidth":200,'alpha':1}
                    )
ax.set(xlabel='Binomial', ylabel='Frequency')
plt.title("伯努利分布(n=1的二项分布)")
plt.show()码片

几何分布

在n次伯努利实验中，第k次实验才得到第一次成功的概率分布。其中：P(k) = (1-p)^(k-1)*p

p = 0.6
x = np.arange(geom.ppf(0.01, p),geom.ppf(0.99, p)+1)
plt.plot(x, geom.pmf(x, p),'o')
plt.title(u'几何分布概率质量函数')
plt.show()