模拟退火算法详解

举个例子

1、求一个给定函数的最值问题

求函数 y = 11sin(x) + 7cos(5x) 在[6, 6] 内的最大值

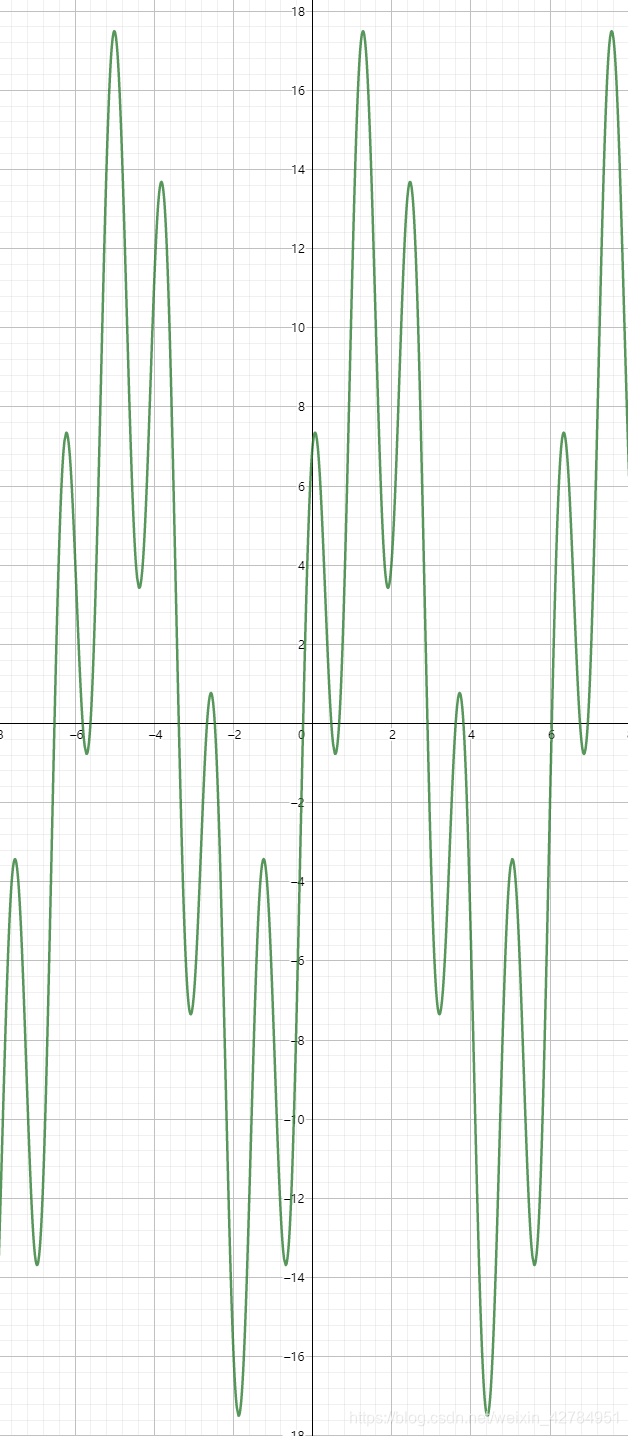
对于此问题，我们可以使用穷举方法，针对x，每次增长一个固定长度: [-10, -9.9999, ....., 9.9999, 10]，然后对每个值代入进行计算，从而找到它最大值比较接近的点。似乎不是特别复杂。

那么当变数量有三个变量时， z= 11sin(x) + 7cos(5y)，从图我们可以看到函数复杂度大大增加，穷举也变得更加困难。

显而易见，当有三十个变量时，穷举的时间复杂度已经提高到难以解决的地步。

2、旅行商问题

假设有一个旅行商人要拜访N个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径为所有路径之中的最小值。

假如我们使用枚举法，先走完所有的路径，然后选出最短的一条路径。从初始点出发的周游路线一共有(n-1)!条，即等于除初始结点外的n-1个结点的排列数，因此旅行商问题是一个排列问题。通过枚举(n-1)!条周游路线，从中找出一条具有最小成本的周游路线的算法，其计算时间显然为O(n!)。

那当有38个城市的时候，对应的计算量是10^44次，假设我们的计算机每秒进行十亿次计算，那么穷尽所有结的时间大于1亿年。

因此当变量数较多时，使用穷举法要耗费大量的时间，是不可能在实际情况下解决问题的。因此就引出了启发式搜索。

启发式搜索

那么什么是启发式搜索呢，它又和盲目搜索有哪些不同？

按照预定的策略实行搜索，在搜索过程中过去的中间信息不用来改进策略，成为盲目搜索，如上面介绍的穷举法为盲目搜索。反之利用中间信息来改进搜索策略则称之为启发式搜索。下面我们要介绍的爬山算法和模拟退火算法就是启发式搜索算法中的一种。

爬山算法

介绍模拟退火前，先介绍爬山算法。爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。 爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。如下图，在处于当前解时，爬山法会同时比较向左走和向右走两种，当发现向右走得到的值会得到更优的解，因此会一直向右走直到找到局部最优解，爬山法搜索到局部最优解后，就会停止搜索，因为在局部最优解这个点，无论向哪个方向小幅度的移动，都无法得到更优解。

模拟退火算法

不同于爬山法，模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。如上图中，在处于局部最优解时，会以一定的概率接受点到A和解B的移动。也许经过几次这样的不是局部最优的移动后会到达最优解，于是就跳出了局部最大值A。

举个例子：

求函数 y = 11sinx + 7cos(5x) 在[-6,6] 内的最大值

假设当前解位于局部最优点B, 其对应的$x_i$所得到函数值为发$f(x_i)$，在A点附近随机找到一个新的解$x_j$，对应的函数值为$f(x_j)$，现在A点位于局部最优解，可以看到无论向左移动还是向右移动都会使$f(x_i)>f(x_j)$，如果直接拒绝，是无法找到最大值的。因此我们直接定义一个接受的概率p，p位于[0,1]之间，且$f(x_i)$和$f(x_{}$