本文介绍了蚁群算法在解决旅行商问题（TSP）中的应用，概述了算法的基本原理，包括蚂蚁如何依据信息素浓度和启发式因子选择路径，以及禁忌表和信息素更新策略。提供了MATLAB和C++两种编程语言的实现示例，其中C++部分的路径绘制使用了OpenCV库。
蚁群算法的直观理解就是：m只蚂蚁分别走遍n个城市，每只蚂蚁根据信息素浓度和启发式因子得出的概率p选择下一座城市。禁忌表Tabu经过一次迭代就更新一次。信息素浓度Tau经过一次迭代就更新一次（蚁周算法）。
典型的MATALB实现：
%%%一个旅行商人要拜访全国31个省会城市，需要选择最短的路径%%%%
%%%蚁群算法解决TSP问题%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
m=50; %% m 蚂蚁个数
Alpha=1; %% Alpha 表征信息素重要程度的参数
Beta=5; %% Beta 表征启发式因子重要程度的参数
Rho=0.1; %% Rho 信息素蒸发系数
NC_max=200; %%最大迭代次数
Q=100; %%信息素增加强度系数
C=[
1304 2312;
3639 1315;
4177 2244;
3712 1399;
3488 1535;
3326 1556;
3238 1229;
4196 1004;
4312 790;
4386 570;
3007 1970;
2562 1756;
2788 1491;
2381 1676;
1332 695;
3715 1678;
3918 2179;
4061 2370;
3780 2212;
3676 2578;
4029 2838;
4263 2931;
3429 1908;
3507 2367;
3394 2643;
3439 3201;
2935 3240;
3140 3550;
2545 2357;
2778 2826;
2370 2975
];%%31个省会坐标
%%-------------------------------------------------------------------------
%% 主要符号说明
%% C n个城市的坐标，n×2的矩阵
%% NC_max 最大迭代次数
%% m 蚂蚁个数
%% Alpha 表征信息素重要程度的参数
%% Beta 表征启发式因子重要程度的参数
%% Rho 信息素蒸发系数
%% Q 信息素增加强度系数
%% R_best 各代最佳路线
%% L_best 各代最佳路线的长度
%%=========================================================================
%% 第一步：变量初始化
n=size(C,1);%n表示问题的规模（城市个数）
D=zeros(n,n);%D表示完全图的赋权邻接矩阵
for i=1:n
for j=1:n
if i~=j
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
else
D(i,j)=eps; %i=j时不计算，应该为0，但后面的启发因子要取倒数，用eps（浮点相对精度）表示
end
D(j,i)=D(i,j); %
end
end
Eta=1./D; %Eta为启发因子，这里设为距离的倒数
Tau=ones(n,n); %Tau为信息素矩阵
Tabu=zeros(m,n); %存储并记录路径的生成
NC=1; %迭代计数器，记录迭代次数
R_best=zeros(NC_max,n); %各代最佳路线
L_best=inf.*ones(NC_max,1); %各代最佳路线的长度
L_ave=zeros(NC_max,1); %各代路线的平均长度
while NC<=NC_max %停止条件之一：达到最大迭代次数，停止
%%第二步：将m只蚂蚁放到n个城市上
Randpos=[]; %随即存取
for i=1:(ceil(m/n))
Randpos=[Randpos,randperm(n)]; %执行两次操作之后Randpos的维度为1*62
end
Tabu(:,1)=(Randpos(1,1:m))';
%%第三步：m只蚂蚁按概率函数选择下一座城市，完成各自的周游
for j=2:n %所在城市不计算
for i=1:m
visited=Tabu(i,1:(j-1)); %记录已访问的城市，避免重复访问
J=zeros(1,(n-j+1)); %存储待访问的城市
P=J; %待访问城市的选择概率分布
Jc=1;
for k=1:n %找到未访问的城市，并存在数组J中
if isempty(find(visited==k, 1)) %开始时置0 find函数返回在visited数组中k所在的位置 没有则返回0 1表示只找1次
J(Jc)=k;
Jc=Jc+1; %访问的城市个数自加1
end
end
%下面计算待选城市的概率分布
for k=1:length(J)
P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);
end
P=P/(sum(P)); %更新待访问城市概率数组中元素的值
%按轮盘赌法选取下一个城市
Pcum=cumsum(P); %cumsum，元素的逐次累加和
Select=find(Pcum>=rand);%选择概率相对较大的那个节点
to_visit=J(Select(1));
Tabu(i,j)=to_visit;
end
end
if NC>=2
Tabu(1,:)=R_best(NC-1,:);%保留一下上次最优路线至tabu第一行，保障本次迭代情况不至于太差
end
%%第四步：记录本次迭代每只蚂蚁所走距离L，记录每次迭代最佳路线距离L_best和最佳路线信息R_best
L=zeros(m,1); %开始距离为0，m*1的列向量
for i=1:m
R=Tabu(i,:);
for j=1:(n-1)
L(i)=L(i)+D(R(j),R(j+1)); %原距离加上第j个城市到第j+1个城市的距离
end
L(i)=L(i)+D(R(1),R(n)); %一轮下来后走过的距离
end
L_best(NC)=min(L); %最佳距离取最小
L_ave(NC)=mean(L); %此轮迭代后的平均距离
pos=find(L==L_best(NC));
R_best(NC,:)=Tabu(pos(1),:); %此轮迭代后的最佳路线
NC=NC+1 %迭代继续
%%第五步：更新信息素
Delta_Tau=zeros(n,n); %开始时信息素为n*n的0矩阵
for i=1:m
for j=1:(n-1)
Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
%此次循环在路径（i，j）上的信息素增量
end
Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
%.此次循环在整个路径上的信息素增量
end
Tau=(1-Rho).*Tau+Delta_Tau; %考虑信息素挥发，更新后的信息素
%%第六步：禁忌表清零
Tabu=zeros(m,n); %直到最大迭代次数
end
%%第七步：输出结果
Pos=find(L_best==min(L_best)); %找到最佳路径（非0为真）
Shortest_Route=R_best(Pos(1),:)%最大迭代次数后最佳路径
Shortest_Length=L_best(Pos(1)) %最大迭代次数后最短距离
%% 画出路线图，和L_best，L_ave迭代曲线
figure(1)
subplot(1,2,1) %绘制第一个子图形
N=length(Shortest_Route);
scatter(C(:,1),C(:,2));
for i = 1:size(C,1)
text(C(i,1),C(i,2),[' ' num2str(i)]);
end
hold on
plot([C(Shortest_Route(1),1),C(Shortest_Route(N),1)],[C(Shortest_Route(1),2),C(Shortest_Route(N),2)],'g')
hold on
for ii=2:N
plot([C(Shortest_Route(ii-1),1),C(Shortest_Route(ii),1)],[C(Shortest_Route(ii-1),2),C(Shortest_Route(ii),2)],'g')
hold on
end
title('旅行商问题优化结果 ')
subplot(1,2,2) %绘制第二个子图形
plot(L_best)
hold on %保持图形
plot(L_ave,'r')
title('平均距离和最短距离') %标题
C++实现：
#include <iostream>
#include <fstream>
#include <stdlib.h>
#include <time.h>
#include <stdio.h>
#include <vector>
#include <algorithm>
#include "draw.h"
using namespace std;
#define m 100 //蚂蚁的个数
#define n 31 //城市的数量
const int NC_max = 100; //最大迭代次数
const double Alpha = 1; //表征信息素重要程度的参数
const double Beta = 5; //表征启发式因子重要程度的参数
const double Rho = 0.1; //信息素蒸发系数
const double Q = 100; //信息素增加强度系数
const double C[n][2] = //各个城市的坐标数据
{ { 1304, 2312 },
{ 3639, 1315 },
{ 4177, 2244 },
{ 3712, 1399 },
{ 3488, 1535 },
{ 3326, 1556 },
{ 3238, 1229 },
{ 4196, 1004 },
{ 4312, 790 },
{ 4386, 570 },
{ 3007, 1970 },
{ 2562, 1756 },
{ 2788, 1491 },
{ 2381, 1676 },
{ 1332, 695 },
{ 3715, 1678 },
{ 3918, 2179 },
{ 4061, 2370 },
{ 3780, 2212 },
{ 3676, 2578 },
{ 4029, 2838 },
{ 4263, 2931 },
{ 3429, 1908 },
{ 3507, 2367 },
{ 3394, 2643 },
{ 3439, 3201 },
{ 2935, 3240 },
{ 3140, 3550 },
{ 2545, 2357 },
{ 2778, 2826 },
{ 2370, 2975 }
};
double D[n][n]; //表示完全图的邻接矩阵
double Eta[n][n]; //表示启发式因子，为D中距离的倒数
double DeltaTau[n][n]; //表示启发式因子的变化量
double Tau[n][n]; //路径上面信息素的浓度
int Tabu[m][n]; //禁忌表，存储走过的路径
double L_best[NC_max]; //存储每次迭代的路径的最短长度
double L_ave[NC_max]; //存储每次迭代的路径的平均长度
int R_best[NC_max][n]; //存储每次迭代的最佳路线
void ValueInit(void) //变量初始化函数
{
for (int i = 0; i < n; i++) //初始化 D[n][n]
{
for (int j = 0; j < n; j++)
{
if (i != j)
D[i][j] = pow(pow((C[i][0] - C[j][0]), 2) + pow((C[i][1] - C[j][1]), 2), 0.5);
else
D[i][j] = DBL_EPSILON;
}
}
for (int i = 0; i < n; i++) //初始化 Eta[n][n]
for (int j = 0; j < n; j++)
Eta[i][j] = 1.0 / D[i][j];
for (int i = 0; i < n; i++) //初始化 DeltaEta[n][n]
for (int j = 0; j < n; j++)
DeltaTau[i][j] = 0;
for (int i = 0; i < n; i++) //初始化 Tau[n][n]
for (int j = 0; j < n; j++)
Tau[i][j] = 1.0;
for (int i = 0; i < m; i++) //初始化 Tabu[m][n]
for (int j = 0; j < n; j++)
Tabu[i][j] = 0;
}
void ValueDisplayTabu(int (*p)[n]) //禁忌表，存储走过的路径, 显示函数
{
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
cout << *(*(p + i) + j) << ' ';
}
cout << endl;
}
}
void ValueDisplayTau(double(*p)[n]) //信息素的浓度,显示函数
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cout << *(*(p + i) + j) << ' ';
}
cout << endl;
}
}
double rnd(double lower, double uper) //生成lower和uper之间的一个double类型随机数
{
return (rand() / (double)RAND_MAX) * (uper - lower) + lower;
}
int main()
{
//第一步：进行变量的初始化
ValueInit();
int NC = 0;
while(NC < NC_max)
{
//第二步：将m只蚂蚁随机放到n个城市上
vector<int> temp;
for (int i = 0; i < ceil((double)m / (double)n); i++)
{
for (int j = 0; j < n; j++)
temp.push_back(j);
}
random_shuffle(temp.begin(), temp.end()); //打乱temp数组中元素的次序
for (int i = 0; i < m; i++)
{
Tabu[i][0] = temp[i];
}
//第三步：m只蚂蚁按概率函数选择n中的下一座城市，完成各自的周游
for (int j = 1; j < n; j++)
{
for (int i = 0; i < m; i++)
{
vector<int> visited; //第i只蚂蚁已访问过的城市
vector<int> J; //第i只蚂蚁待访问的城市
vector<double> P; //第i只蚂蚁待访问的城市的概率
double Psum = 0.0; //概率值和
double rate = 0.0; //随机数
double choose = 0.0; //轮盘赌算法累加值
int to_visit; //下一个要去的城市
for (int k = 0; k < j; k++)
visited.push_back(Tabu[i][k]); //visited初始化
for (int k = 0; k < n; k++)
{
if (find(visited.begin(), visited.end(), k) == visited.end()) //在visited中没有找到t
{
J.push_back(k); //J初始化
P.push_back(0.0); //P初始化
}
}
for (int k = 0; k < P.size(); k++) //计算去下一座城市的概率
{
P[k] = pow(Tau[visited.back()][J[k]], Alpha) * pow(Eta[visited.back()][J[k]], Beta);
Psum += P[k];
}
rate = rnd(0.0, Psum); //使用轮盘赌算法，挑选下一座要去的城市
for (int k = 0; k < P.size(); k++)
{
choose += P[k];
if (choose > rate)
{
to_visit = J[k];
break;
}
}
Tabu[i][j] = to_visit; //更新禁忌表
}
}
//第四步：记录本次迭代蚂蚁行走的路线数据
double L[m]; //记录本代每只蚂蚁走的路程，并初始化
for (int i = 0; i < m; i++)
{
L[i] = 0.0;
}
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n - 1; j++)
{
L[i] += D[Tabu[i][j]][Tabu[i][j + 1]];
}
L[i] += D[Tabu[i][0]][Tabu[i][n - 1]];
}
double min_value = L[0]; //声明求本代所有蚂蚁行走距离最小值的临时变量
double sum_value = L[0]; //声明求本代所有蚂蚁行走距离总值的临时变量
int min_index = 0; //记录本代所有蚂蚁行走距离最小值的下标
for (int i = 1; i < m; i++)
{
sum_value += L[i];
if (L[i] < min_value)
{
min_value = L[i];
min_index = i;
}
}
L_best[NC] = min_value; //每代中路径的最短长度
L_ave[NC] = sum_value / m; //每代中路径的平均长度
for (int i = 0; i < n; i++)
{
R_best[NC][i] = Tabu[min_index][i]; //记录每代最短的路径数据
}
cout << NC << ": L_best is " << L_best[NC] << ' ' << "L_ave is " << L_ave[NC] << endl; //打印各代距离信息
NC++; //迭代继续
//第五步：更新信息素
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n - 1; j++)
{
DeltaTau[Tabu[i][j]][Tabu[i][j + 1]] += Q / L[i]; //此次循环在整个路径上的信息素增量
}
DeltaTau[Tabu[i][n - 1]][Tabu[i][0]] += Q / L[i];
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
Tau[i][j] = (1 - Rho) * Tau[i][j] + DeltaTau[i][j]; //考虑信息素挥发，更新后的信息素
}
}
for (int i = 0; i < m; i++) //禁忌表清零
for (int j = 0; j < n; j++)
Tabu[i][j] = 0;
}
//第六步：把结果画出来
double min_L = L_best[0]; //所有迭代中最短距离
int min_L_index = 0; //所有迭代中最优路径的下标
int Shortest_Route[n]; //所有迭代中的最优路径
for (int i = 0; i < NC; i++)
{
if (L_best[i] < min_L)
{
min_L = L_best[i];
min_L_index = i;
}
}
cout << "The length of the shortest route is " << min_L << endl;
cout << "The number of iteration is " << min_L_index << endl;
cout << "The Shortest route is： " << endl << "start";
for (int i = 0; i < n; i++) //所有迭代中的最优路径
{
Shortest_Route[i] = R_best[min_L_index][i];
cout << " -> " << Shortest_Route[i];
}
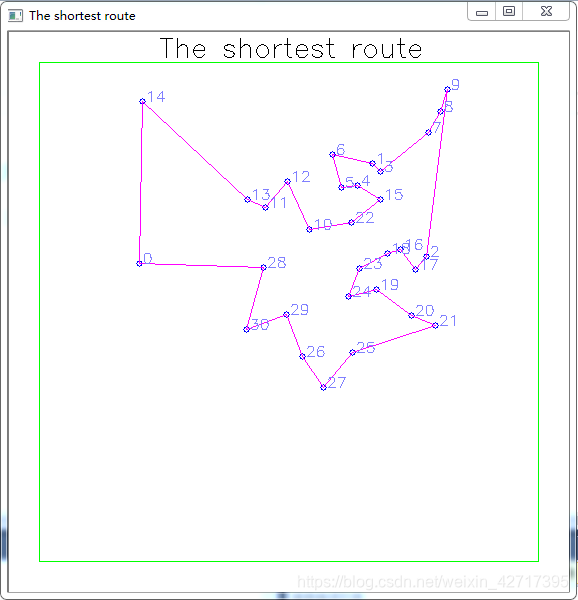
//draw_route(C, Shortest_Route); //画出来最优的路线
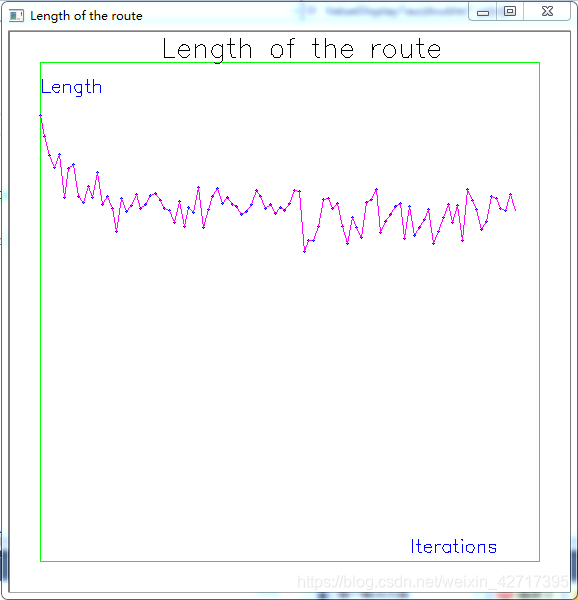
//draw_Lbest(NC_max, L_best); //画出来各代最优距离的曲线
system("pause");
return 0;
}
注：最后我是用opencv画出曲线的，可以注释掉
扫一扫
420
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
