这篇论文评估了一款连接到80通道列表模式读出系统的大型视场伽马相机，适用于25-511keV能量范围。研究涵盖了从基座减法、数字光电倍增管增益均衡到能量和空间校正的详细数据处理方法，展示了良好的能量分辨率、空间分辨率和均匀性。系统在小动物成像和正电子发射器应用中具有潜力。
Evaluation of a 25-511keV List Mode Readout System for a Large Field-of-View Gamma Camera
【25-511keV列表模式读数的评估大型视野伽马相机的系统】
原文链接：https://sci-hub.st/10.1109/NSSMIC.2010.5874166
我们评估了连接到新的80通道列表模式读出系统的大视场伽马相机(9.5毫米厚的NaI(Tl)晶体)的性能。该装置的最终目标是在小型动物扫描仪中同时对正电子发射器(511千电子伏)和单光子发射示踪剂(25-400千电子伏)进行亚毫米成像。我们的测试伽马相机中的所有55个光电倍增管(PMT)都已插入读出系统的通道，该系统在输出端给出闪烁晶体中伽马射线事件的PMT信号的数字化电荷积分值。除此之外，我们还开发了数据处理和校准方法，以从检测器获得校正后的图像。为了在不丢失相关信息的情况下最小化列表文件的大小，只有那些高于基值的PMT值才会被写入磁盘。在离线分析中，我们通过结合从校准数据获得的能量、线性和均匀性校正，使用电荷质心发现算法来估计伽马相互作用的位置和能量。
我们严格按照NEMA NU 1-2007标准评估了从27keV伏(I-125)到511keV(Na-22)的能量范围内的性能。我们发现空间分辨率从7.1毫米(27keV)到3.0毫米(511keV)不等。能量分辨率范围从22.7%(27keV)到9.7%(511keV)。在所有能量的有用视场(UFOV)上，发现差分空间线性度优于0.3毫米。在整个能量范围内，积分和微分均匀性分别优于2.8%和1.8%。
我们的读数系统和软件在空前的各种能量范围内均显示出良好的性能，并且仅针对27、140和511 keV采集了校准数据。通过对单个光电倍增管信号运行更复杂的统计定位算法，我们相信最终可以用相同的探测器硬件扩大UFOV，并且空间和能量分辨率都可以略有提高。
1 介绍
对于小动物成像，临床伽马探测器的应用在使用大范围能量方面提出了新的挑战。27KeV周围的低能同位素不会应用在人体诊断应用中，因为在该能量下发射的伽马射线在软组织中具有大约1cm的平均路径长度。如果他们在人体内发射，他们不会到达探测器，因为他们必须经过厘米级的距离。然而，在小动物应用中，对于I-125这样的同位素（其光峰在30keV附近），越来越需要标记药物分子。
另一方面，最近引入的专用针孔准直器可以应用于正电子发射体产生的511keV的高能光子，为这种探测器开辟了新的应用，这种探测器在历史上被限制在70-400keV的能量范围内。仅对于低成本的PET兼容系统，晶体比本研究中的晶体厚的伽马相机的性能已在70-511keV范围内进行了评估。此外，伽马照相机用于正电子发射器的符合成像的使用已经被研究，呈现出一些限制，特别是关于计数率能力，这在针孔PET中不再是一个问题。
商业上可获得的临床伽马相机不允许如此宽的能量范围，也不提供来自读出电子设备的数字光电倍增管值，这一事实促使我们开发一种读出系统，我们将能够为这一大能量范围改进定位和校准方法。
在这项工作中，我们评估了25-511keV能量范围内的临床伽马相机的性能，该相机连接到列表模式读出系统，该系统设计和配置为在如此宽的能量范围内实现良好的响应。当晶体中发生伽马射线相互作用时，电子器件给出所有光电倍增管的数字化电荷积分值。由于正确的校准对于获得最佳结果非常重要，我们还介绍了本评估中使用的开发校准方法。
2 材料
我们使用了一个伽马相机，它有一个9.5毫米厚的NaI(TI)晶体和一个23x19英寸的视场(FOV)。它有55个光电倍增管:49个3英寸直径，6个2英寸直径。它们已经被插入到我们的80通道列表模式读出系统的通道中，如果来自一组16个通道的和信号高于阈值，就会触发该系统。在检测到有效事件后，光电倍增管的输出信号被积分一段预设时间。这些值被数字化并传送到采集计算机，在那里基座减法和光电倍增管增益均衡被在线执行。然后，列表模式数据可通过复杂的校准和校正算法进行离线处理，以估计事件位置和能量。超级列表模式一词可用于电子设备提供的数据格式，因为越来越多的术语将其与列表模式的历史含义（列表项是位置和能量估计）区别开来。
3 方法
3.1 数据处理
我们的校准方法包括五个步骤。前两个(基座减法和数字光电倍增管增益均衡)处理来自电子设备的原始数据，并在线完成。其他(能量、线性和均匀性校正)离线完成，并使用估计的空间坐标和伽马相互作用的能量。每个校正步骤都涉及校准文件，这些文件必须在后续步骤进行之前应用于采集的数据。
3.2 在线处理
3.2.1 基座减法
在电荷积分期间，在硬件中应用电流偏移，以避免负电荷的积分。这种偏移在通道之间略有不同，主要是由于组件的公差(图1)
基座的测量使用周期时钟来触发系统，而不是来自相机的信号。来自每个通道的数据被拟合到高斯函数以获得平均基座值。为了使所有通道达到共同的零参考，在伽马测量中，从通道值中在线减去基座值。
3.2.2 数字光电倍增管增益均衡
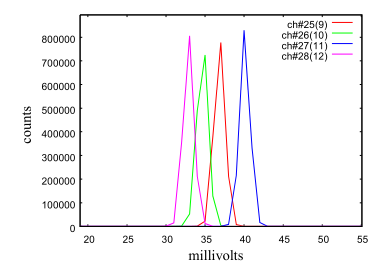
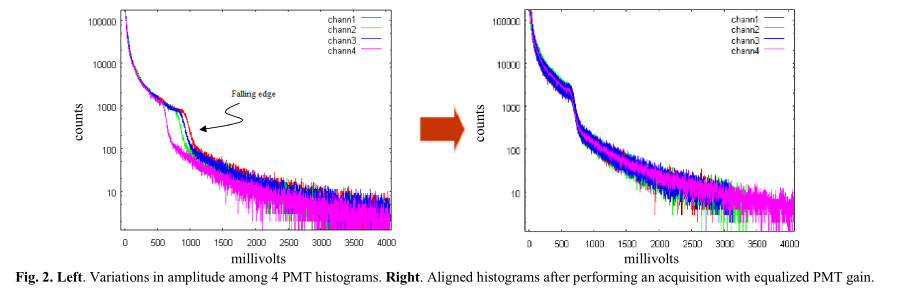
通过用均匀的Tc-99m放射源照射整个探测器表面，每个光电倍增管直方图并不显示相同的毫伏幅度(图2，左侧)。对于每个光电倍增管，我们设置一个增益校正因子来均衡所有光电倍增管响应。均衡过程包括以下步骤:
a)拾取每个直方图(FEi)的下降沿。我们假设该点是拐点，因此我们在直方图的二阶导数中寻找符号的变化，该变化先前已经用移动平均滤波器平滑，以提供对噪声的鲁棒性。
b)平均所有直方图下降沿的位置(FEavg)。
c)对于每个光电倍增管，我们定义了一个增益校正因子，即所有直方图的平均下降沿与每个直方图的下降沿之比Gi= FEavg/FEi
来自读出电子设备的每个数字化光电倍增管值将在线乘以在该校准步骤中计算的增益系数。
3.2.3 列表模式格式
对于每个检测到的事件，我们只在基座减法和非零增益校正后将PMT值写入磁盘。与从电子设备中写入所有原始数据相比，这将大大减少列表文件的大小。我们已经测试了在上述标准下对图像形成有贡献的偏振模色散的数量是介于10和20之间的可变数量。由于我们使用3字节/PMT (1字节用于PMT标识符，2字节(12位)用于PMT值)，我们最终有30-60字节/事件，而不是由读出系统发送的176字节/事件的固定大小。
3.3 离线处理
3.3.1 事件能量和位置
我们使用基于阈值的质心估计算法。事件能量Eest的估计首先通过对我们的伽马相机的所有55个光电倍增管通道(Pi)求和来确定。然后阈值ET被设置为ET=T*Eest，其中T被设置为0.04(即总事件能量的4%)。
E
e
s
t
=
∑
i
=
1
55
P
i
E_{est}=\sum_{i=1}^{55}{P_i}
Eest=i=1∑55Pi
E T = T E e s t E_{T}=TE_{est} ET=TEest
我们假设，只有ET值以上的才有助于γ相互作用的定位[。低于ET的PMT预计会引入噪声，因此设置为零。位置计算以浮点精度离线执行(公式3和4)。Ci,x和Ci,y是512x512像素矩阵中PMTi中心位置的x和y坐标。
X
=
∑
P
i
>
E
T
C
i
,
x
(
P
i
−
E
T
)
/
∑
P
i
>
E
T
(
P
i
−
E
T
)
X={\sum_{P_i>E_T}{C_{i,x}(P_i-E_T)}}/{\sum_{P_i>E_T}{(P_i-E_T)}}
X=Pi>ET∑Ci,x(Pi−ET)/Pi>ET∑(Pi−ET)
Y = ∑ P i > E T C i , y ( P i − E T ) / ∑ P i > E T ( P i − E T ) Y={\sum_{P_i>E_T}{C_{i,y}(P_i-E_T)}}/{\sum_{P_i>E_T}{(P_i-E_T)}} Y=Pi>ET∑Ci,y(Pi−ET)/Pi>ET∑(Pi−ET)
在采集10幅图像(Tc-99m)后，选择0.04的T值，T值范围为0至0.09。用于线性校准的模型(见第三节。C.3)被放置在照相机前面。选择阈值的标准仅仅是视觉检查:当阈值低于T=0.04时，图像中的斑点看起来彼此靠近，并且图像存在全局收缩，导致定位精度的损失。当阈值高于0.04时，质心估计开始无法区分两个相邻的幻像孔。
为了将能量信息存储在有限的位数中，我们将Eest扩展到256个能量仓。
3.3.2 能量校准
观察探测器每个位置的能量响应Eest，我们观察到单能同位素成像时光电峰光谱位置的变化。我们的方法为探测器中的2×2像素(2.38mm2)区域定义了局部能量校准因子。我们分别对3个洪水源(I-125(27千电子伏)、Tc-99(140千电子伏)和Na-22(511千电子伏))进行成像，以获得每个局部区域至少1000个光峰计数。对于这些数据，我们可以为每个区域拟合二阶多项式，以计算能量仓和keV之间的关系。
E
(
k
e
V
)
=
a
∗
c
h
2
+
b
∗
c
h
+
c
E(keV)=a*ch^2+b*ch+c
E(keV)=a∗ch2+b∗ch+c
我们发现，虽然线性拟合对于相对较短的能量范围就足够了，但是当观察25-511千电子伏的范围时，多项式拟合提供了更精确的能量转换。
整个检测器上系数的平均值(+/-标准偏差)如下所示。请注意二次系数的较小值，它在较高的能量下变得相关(相对于线性拟合)。
a=0.0012±0.0002; b=2.69±0.13;c=1.28±1.0
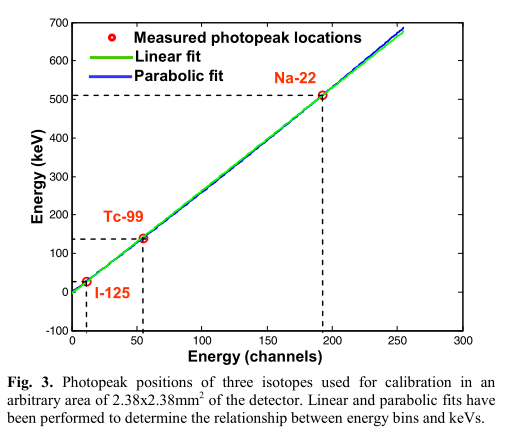
图3 在探测器2.38x2.38mm2的任意区域内用于校准的三种同位素的光峰位置。线性拟合和抛物线拟合被用来确定能量仓和千电子伏之间的关系。
3.3.3 空间线性校正
在伽玛相机中，使用标准质心方法进行事件定位的准确性因视场而异。为了进行校正，我们在摄像机前放置一个正交孔模型(2.25毫米孔直径，15毫米间距)，由Tc-99m光源均匀照射。我们获得了如图5(左)所示的失真图像。
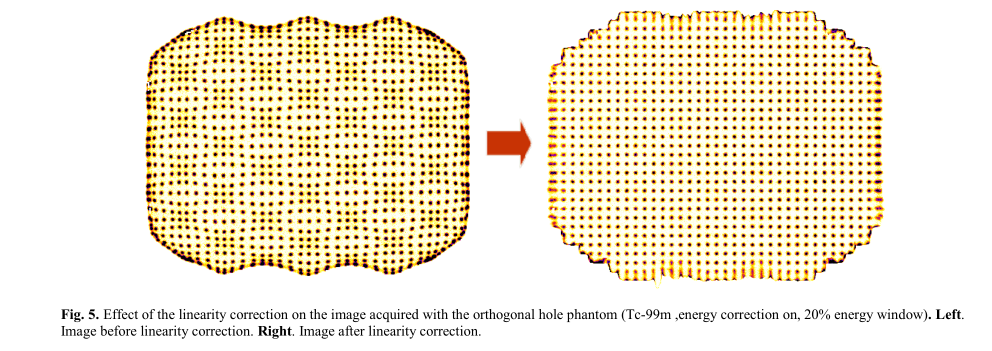
图5 线性校正对用正交孔模型(Tc-99m，能量校正，20%能量窗)获得的图像的影响。左图：线性校正前的图像。右图：线性校正后的图像。
本工作中应用的线性校准遵循以下程序:
a.以512x512像素的矩阵大小生成一个与模型中孔洞的真实位置相匹配的规则网格。
b.确定图像中每个投影点的最大亮度位置。应用高斯滤波器来消除高频，并从中减去噪声阈值(设置为图像中最大值的20%)。沿X和Y方向对图像进行两次扫描，寻找相对最大值，得到最大亮度图。我们假设这些最大值确定了斑点中心。
c.通过连接上一步计算的点，将整个图像分割成四边形(图4)
图4 未校正图像的细节，用于校准，显示四边形的不规则图案(红线)。绿线的交点表示投影点在没有空间扭曲的情况下应该所处的位置。
d.需要修正的基本上是几何变换。对于每个不规则四边形，可以通过双线性变换(等式6)获得其规则等价四边形。对于每对四边形，可以从四边形的4个角计算出变换T。(图6)
KaTeX parse error: Undefined control sequence: \matrix at position 74: …quad T= \left[ \̲m̲a̲t̲r̲i̲x̲{ \C_{11} & C…
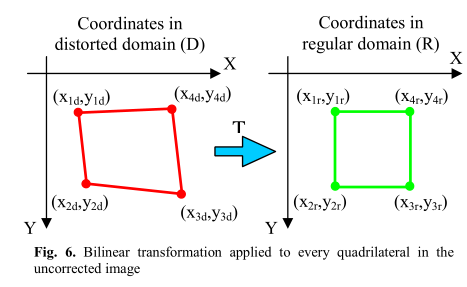
图6 双线性变换应用于未校正图像中的每个四边形
e.对图像中的每一对(X，Y)应用这些变换，并计算X和Y坐标的偏移，以校正失真，并将它们存储在512x512查找表(LUT)中。
L
U
T
x
(
x
D
,
y
D
)
=
x
R
−
x
D
LUT_x(x_D,y_D)=x_R-x_D
LUTx(xD,yD)=xR−xD
L U T y ( x D , y D ) = y R − y D LUT_y(x_D,y_D)=y_R-y_D LUTy(xD,yD)=yR−yD
f.我们的查找表具有有限的分辨率，即512x512，但重建的事件坐标是以浮点精度计算的。如果这些坐标落在查找表的4个像素之间，我们应用双三次插值来获得所需的位移。
S
H
I
F
T
(
x
D
,
y
D
)
=
∑
n
=
−
1
2
∑
m
=
−
1
2
L
U
T
(
i
+
n
,
j
+
n
)
∗
P
(
n
−
a
)
∗
P
(
b
−
m
)
SHIFT(x_D,y_D)=\sum_{n=-1}^{2}\sum_{m=-1}^{2}{LUT(i+n,j+n)*P(n-a)*P(b-m)}
SHIFT(xD,yD)=n=−1∑2m=−1∑2LUT(i+n,j+n)∗P(n−a)∗P(b−m)
w h e r e P ( k ) = 1 6 ( ( C ( k + 2 ) ) 3 − 4 ∗ ( C ( k + 1 ) ) 3 + 6 ( C ( k ) ) 3 − 4 ( c ( k − 1 ) ) 3 ) w h e r e c ( k ) = m a x ( 0 , k ) where \quad P(k)=\frac{1}{6}((C(k+2))^3-4*(C(k+1))^3+6(C(k))^3-4(c(k-1))^3)\quad where c(k)=max(0,k) whereP(k)=61((C(k+2))3−4∗(C(k+1))3+6(C(k))3−4(c(k−1))3)wherec(k)=max(0,k)
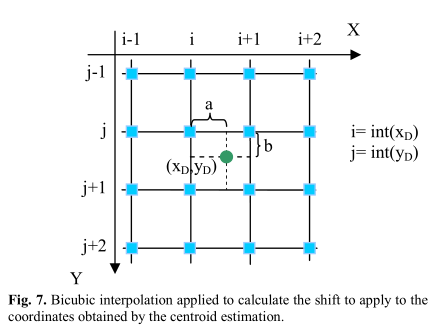
图7 双三次插值用于计算应用于质心估计获得的坐标的偏移。
g.最后，每个事件的坐标根据以下内容进行校正:
(
x
c
o
r
r
,
y
c
o
r
r
)
=
(
x
D
+
S
H
I
F
T
x
(
x
D
,
y
D
)
,
y
D
+
S
H
I
F
T
y
(
x
D
,
y
D
)
)
(x_corr,y_corr)=(x_D+SHIFT_x(x_D,y_D),y_D+SHIFT_y(x_D,y_D))
(xcorr,ycorr)=(xD+SHIFTx(xD,yD),yD+SHIFTy(xD,yD))
我们使用从Tc-99m计算的每个同位素的查找表。
3.3.4 均匀性校准
在应用上述校正之后，在用均匀洪水源获取的图像中仍然存在不均匀性。最后一次校正是基于计算洪水场图像(Navg)中每个像素的平均计数。为了避免统计波动，必须在光峰窗口中获得至少500个计数/像素。对于洪水源图像中具有Ni计数的每个像素，均匀性校正因子为:UCFi= Navg/ Ni，这意味着Navg以下的像素产生大于1的校正因子，而Navg以上的像素产生小于1的校正因子。
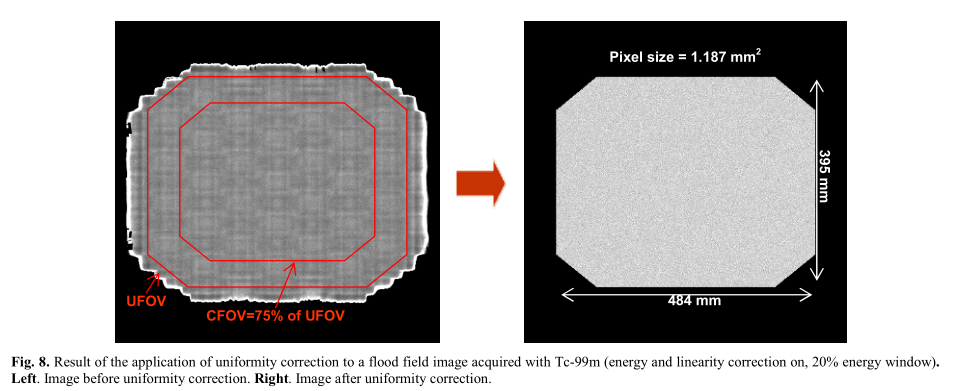
对Tc-99m获得的洪水场图像进行均匀性校正的结果(能量和线性校正开启，20%能量窗口)。左：均匀性校正前的图像。右：均匀性校正后的图像。
我们计算步骤4中使用的每种同位素的均匀性图:I-125、Tc-99、Na-22。在这一步中，我们还将图像遮挡到有用的视场(UFOV)，我们将其定义为484x395mm2。
3.4 测量
一旦摄像机被校准并且所有校准文件被生成，我们就对能量分辨率、空间分辨率、差分空间线性度和洪水场均匀性进行测量。我们严格遵循NEMA伽马相机性能测量标准，因此我们仅提及偏离标准的步骤。
为了测量空间分辨率和线性度，NEMA建议使用覆盖整个有用视场的铅掩模，该掩模具有1毫米宽的平行狭缝和30毫米的间距。我们在伽马相机的中心放置了一个1毫米宽的单缝引线模型(I-125为3毫米厚，Tc-99为4.5厘米厚，Na22为4.5厘米厚)。提供的结果是两次测量的平均值。
为了测量空间差分线性，我们使用了与空间分辨率相同的数据集。所提供的结果是狭缝中等距线扩展函数峰值位置的标准偏差的平均值。
4 结果
4.1 能量分辨率
我们在图9中显示了I-125 (1h采集时间，29000 cps观测计数率)、Tc-99 (1h30 '，17.000 cps)和Na-22(2 h30 '，34000 cps)的三次洪水现场采集的能谱。这些测量不需要如此长的采集时间，但我们后来在相同的数据集上使用，以评估一致性，其中每个像素需要最小数量的计数，以符合NEMA标准。
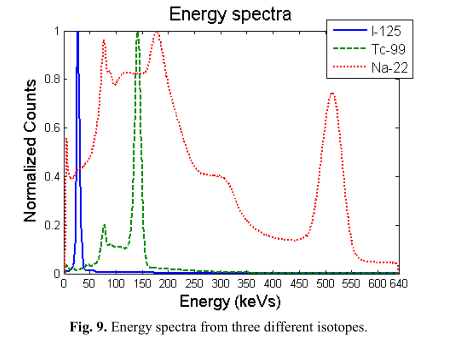
图9。三种不同同位素的能谱。
4.2 空间分辨率和线性度
表1显示了固有空间分辨率和差分线性度的结果。钠-22图像中的背景(尽管模型厚度为4.5厘米)使得无法测量该同位素的FWTM。图10显示了用这些测量获得的一些图像。I-125、Tc-99和Na-22的对称能窗分别为58%、20%和18%。
图10。用单缝体模获得的图像。
表一.空间分辨率和线性结果
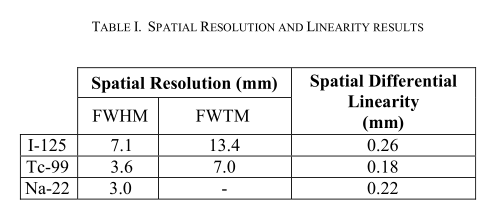
4.3 洪水场均匀性
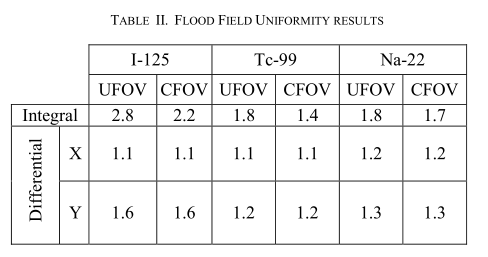
与能量分辨率相同的数据集用于评估洪水场均匀性测量。与第四章相同的能量窗B被应用。我们将图像重新绑定到8.22毫米的像素大小，以便在中心像素中至少有10.000个计数。三种同位素的结果如表2所示。
表二。洪水场均匀性结果
5 讨论和结论
们已经评估了基于光电倍增管的伽马相机的性能，该相机连接到一个新颖的80通道列表模式读出电子系统，具有广泛的能量范围。结果是令人鼓舞的，将该系统应用于具有511千电子伏针孔成像选项的小动物断层扫描系统。此外，我们相信，通过更复杂的定位算法，可以用所提出的电子设备来实现，在空间分辨率和线性方面的性能可以进一步提高。
扫一扫
2255
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
