普林斯顿大学—算法4—学习记录

tips：https://www.cnblogs.com/onepixel/articles/7674659.html十大经典排序算法

 

开发有效算法的流程：

1-建立问题模型 

2-提出算法解决问题

3-运行时间、存储空间不足--找出问题所在--提出新算法

以上为设计和分析希算法的科学途径，找出问题的实质，通过实践验证模型，进而改进模型和方法。

 

2-1 动态连通性问题 Dynamic connectivity

即 并查集问题的模型

连接

连通分量：互相连接的对象的最大集合

java中：创建UF类，包含两个方法：1 实现合并；2 连接查找，返回一个布尔量。构建器需要对象的数量

 由此建立数据结构。

PS：当实现算法时，对象的数量和操作的数量是巨大的，可能有大量合并与连接查找的操作，此时算法的高效尤为重要

  测试：在处理更深层的问题之前，需要检查应用程序接口API的设计。

2-2-快速查找 Quick-find

attention here：

—> union(1,3)把1的内容改成3

—> 合并时，把if语句中的pid写成索引值p

快速查找算法的效率：

查找：常数次

合并：查找他们是否连通-N²次，太慢不可取

2-3- 快速合并

合并具体示例：

attention—>union(根节点，子节点)，当根节点在一个连通分量里，那么子节点连接在连通分量的根节点上；当子节点在一个连通分量里，那么连通分量的根节点连接在包含根节点的连通分量根节点上。

具体实现：

效率：

虽然比快速查找法快速，但也很慢。

当树很高，查找操作代价很大。每个子节点都需要遍历。

 

2-4 快速合并的改进 Quick union improvement

方法1：权重weighting

           任意节点x的深度是以2为底N的对数

方法2：路径压缩 path compression

时间复杂度并不线性，但足够接近线性

并查集问题不存在线性时间算法

2-5 Union find application 应用

渗滤模型percolation

 

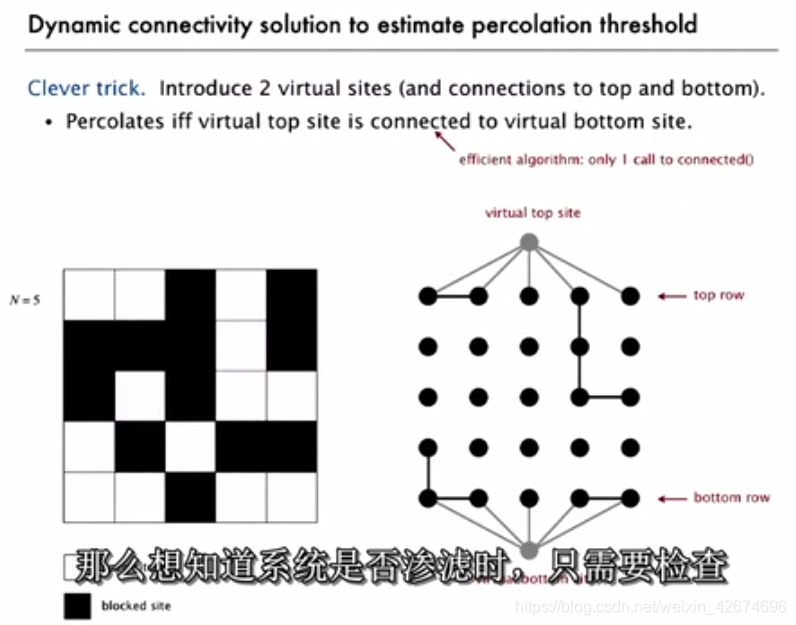
3-1 算法分析

FFT： N log N

N body simulation： N log N

科学方法：

观察

假设：假设一个与观察结果一致的模型

预测：通过假设预测事件

验证预测

证明 重复实验直到假设与观察结果一致

3-2 观察

Q1：如何定量测量程序运行时间。

        java 中 Stopwatch.java类可以检测运行时间

 

三数之和：计算三个输入整数之和为0，ThreeSum.count()计算每次输入大小。

 DoublingTest.：生成一个随机数输入数组，每次数组大小×2，输出运行时间。 DoublingRatio.java类似于ThreeSum.count()，也但同时输出从一种尺寸到下一种尺寸的运行时间比率。

3-3 数学模型

程序的运行时间有两方面因素决定：执行每个语句的成本和每个语句执行频率

Tilde近似：当使用tilde近似时，使公式复杂化的低阶项被忽略。用 ~ f(N) 表示任何被除以y f(N)后接近1的函数，g（N）~f（N）表示 随着N的增大，g（N）/ f（N）接近1 

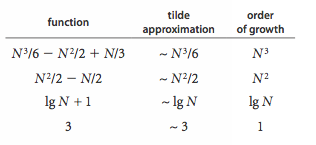
Order-of-growth classifications增长顺序分类：

使用一些结构基元（语句，条件，循环，嵌套和方法调用）来实现算法，因此成本增长的顺序通常只是问题大小N的几个函数之一。

成本模型Cost model：通过阐明定义基本操作的成本模型，我们得到算法的性能。例如？：3-sum问题的适当成本模型是我们访问数组条目的次数，用于读取或写入。

性能：ThreeSum.java 的增长顺序的运行时间 为N ^ 3

建议：3数之和的暴力算法：使用N^3 / 2 数组访问来计算N个数中总和为0的三元组数

设计更快的算法：使用归并排序mergesort 和二进制排序binary search。

                      2数之和： TwoSum.java暴力算法的时间复杂度 N^2.TwoSumFast.java时间复杂度N log N 

                      3数之和： ThreeSumFast.java 时间复杂度N^2 log N 

关于对输入依赖的应对：

对于很多问题来说，程序运行时间很大程度上取决于输入

-输入模型。我们必须人文模拟输入类型，因为模型可能并不现实。

-最坏情况保证。 运行时间小于一个确定值，无论输入的是什么。

-随机算法。提供性能保证的一种方法是引入随机性，例如快速排序和散列。每次运行算法时，都会花费不同的时间。这些保证并不是绝对的，但它们无效的可能性小于您的计算机被闪电击中的可能性。因此，这种保证在实践中与最坏情况保证一样有用。

-摊销分析。对于很多应用，算法的输入可能不仅仅是数据，而是用户的操作顺序。摊销分析为一系列操作提供一种最坏情况下的性能保证。

PS: 在Bag，Stack和Queue的链表实现中 ，所有操作在最坏的情况下都需要一段时间。

PS: 在Bag，Stack和Queue的调整大小数组实现中 ，从空数据结构开始，在最坏的情况下，N个操作的任何序列都需要与N成比例的时间（每个操作的摊销的恒定时间）。

内存使用memory usage

为了估计程序使用多少内存，我们可以计算变量的数量，并根据它们的类型按字节数加权。

对于典型的 64位机器，

-私有类型（primitive types）

-对象（object）

为了计算对象的内存使用情况，我们可以增加每个实例变量使用的内存量添加到每个对象的关联开销中

为了确定对象的内存使用情况，我们将每个实例变量使用的内存量添加到与每个对象关联的开销中，通常为16个字节。此外，内存使用量通常填充为8字节的倍数（在64位机器上）。

-引用。引用通常是对象的内存地址，所以用8字节内存。

-LinkList链表列表。嵌套的非静态（内部）类需要额外的8字节开销（用来对封装实例的引用）。

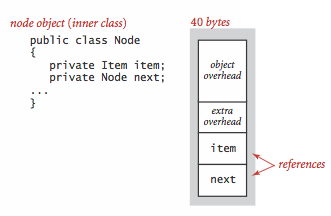
-数组Array。数组被实例化为对象，需要额外的开销。一个原始类型数据的数组需要24字节的头信息（16字节的对象开销，4字节的长度，4字节的填充）以及存储值所需的内存。

-字符串String。长度为N的 Java 7字符串通常使用32个字节（对于String对象）加上24 + 2 N个字节（对于包含字符的数组），总共56 + 2 N个字节。

根据上下文，我们可能会或可能不会计算对象的内存引用（递归）。例如，我们为String对象计算内存中char []数组的内存， 因为在创建字符串时会分配此内存。但是，我们通常不会计算StackOfStrings对象中String对象 的内存，因为String对象是由客户端创建的。 

WEEK2

包、队列、堆栈

1-1 APIs

1-1

泛型 generic

ADT数据集最主要特征是他需要被应用于任何数据类型，在Java中有特定的机制支持这个功能。

每个API中的类名后面的符号<Item>将名称Item定义为类型参数，是客户端使用的某种具体类型的符号占位符。

API中每个类名后面的特殊符号<item>定义item为一个类型参数

Stack<item> 表示 stack of items。

自动装箱autoboxing

可迭代 Iterable

背包bags

先进先出FIFO

pushdown stack

Arithemtic expression evaluation

 

Array and resizing array implementations of collection

Linked list 

stack代码实现：

package com.appjishu.algorithm4j.StackandQueues;

import java.util.Arrays;

public class Stack {
    private int size = 0;
    private  int[] array;

    public Stack(){
        this(10);
    }
    public Stack(int i){
        if(i <= 10){
            i = 10;
        }
        array = new int[i];
    }

    /**
     * 入栈、
     *入栈
     * @paramitem入栈的值
     */
    public void push(int item){
        if(size == array.length){
            array = Arrays.copyOf(array,size * 2); //扩容
        }
        array[size++] = item;
    }

    /**
     * 获取栈顶元素，但不出站
     * @return
     */
    public int peek(){
        if(size == 0){
            throw new IndexOutOfBoundsException("栈已为空"); //异常情况
        }
        return array[size - 1];
    }

    /**
     * 出栈，同时获取栈顶元素
     * @return
     */
    public int pop(){
        int i = peek();
        size--;//是元素个数减一，下次入栈覆盖旧元素的值
        return i;
    }

    /**
     * 栈是否已满
     * @return
     */
    public  boolean isFull(){
        return size == array.length;
    }

    /**
     * 栈是否为空
     * @return
     */
    public boolean isEmpty(){
        return size == 0;
    }
    public  int size(){
        return size;
    }
}

stacktest代码实现

package com.appjishu.test;


import com.appjishu.algorithm4j.StackandQueues.Stack;

public class StackTest {
    public static void main(String[] args){
        Stack stack = new Stack(1);  //设定初始长度1
        stack.push(1);
        stack.push(2);
        System.out.println("栈内的元素个数是（当前数组长度为2）：" + stack.size());

        stack.push(3);
        System.out.println("栈内的元素个数是（当前数组长度为3）：" + stack.size());
        System.out.println("获取栈顶元素："  + stack.peek());
        System.out.println("获取栈顶元素之后的元素个数：" + stack.size());
        System.out.println("出栈元素：  "  +stack.pop());
        System.out.println("出栈后的元素个数：  "+stack.size());

    }
}

queue代码实现

package com.appjishu.algorithm4j.StackandQueues;

public class Queue {
    private final Object[] items;
    private int head = 0;
    private int tail = 0;

    /**
     * 初始化隊列
     * @paramcapacity隊列的長度
     */
    public Queue(int capacity){
        this.items = new Object[capacity];
    }

    /**
     * 入隊
     * @param item
     * @retrun
     */
    public boolean put(Object item){
        if(head == (tail + 1) % items.length){ //隊滿
            return false;
        }
        items[tail] = item;
        tail = (tail + 1) % items.length;//标记向后移动一位
        return true;
    }
    /**
     * 获取头元素，不出队
     * @return
     */
    public Object peek(){
        if(head == tail){//队列为空
            return null;
        }
        return items[head];
    }

    /**
     * 出队
     *@return
     */
    public Object poll(){
        if(head == tail){
            return null;
        }
        Object item = items[head];
        items[head] = null; //把没用的元素赋值空值

        head = (head + 1) % items.length;
        return item;
    }

    public boolean isEmpty(){
        return head == tail;
    }
    public boolean isFull(){
        return head == (tail +1)%items.length;
    }
    public int size(){
        if(tail >= head){
            return tail - head;
        }else{
            return tail + items.length - head;
        }
    }

}

queueTest代码实现

package com.appjishu.test;

import com.appjishu.algorithm4j.StackandQueues.Queue;

public class QueueTest {
    public static void main(String[] args){
        Queue q = new Queue(4);
        System.out.println("队长度 "  + q.size());
        q.put(1000);
        q.put(9999);
        q.put(9998);
        System.out.println("对头元素" + q.peek());
        System.out.println("出队元素" + q.poll());
        System.out.println("队长度" + q.size());
    }
}

2-1 排序