基于MATLAB的机器人学、机器视觉与控制

• 参考书目：《机器人学、机器视觉与控制——MATLAB算法基础》，Peter Corke
• 准备工具：MATLAB，Robotics Toolbox[download]，安装方法参考[blog]

---

根据毕业设计的要求，本文主要讨论机械臂动力学，视觉与控制

一、机械臂运动学

运动学是力学的一个分支，它在不考虑质量和作用力的前提下研究一个刚体，或者由多个刚体组成系统的运动。

1.描述一台机械臂

一个串联机械臂的整个链路是由一组被称为连杆的刚体组成的，这些连杆由关节（运动副）连接起来。每个关节有一个平移（滑动或移动副）或者转动（转动副）的自由度。关节的运动改变了其邻接连杆的相对角度和位置。

• 使用工具箱中的 Link 对象来描述一个机器人连杆：
  

>> L = Link([0, 0.1, 0.2, pi/2, 0])
 
L = 
Revolute(std): theta=q, d=0.1, a=0.2, alpha=1.5708, offset=0

输入向量的元素按顺序为：关节角，连杆偏移，连杆长度，连杆扭转角；第五个元素未指定则默认为转动关节。

• 两连杆机器人
  D-H 参数如下所示，用这些参数创建一个 Link 对象的向量 L：
  

>> L(1) = Link([0 0 1 0]);
>> L(2) = Link([0 0 1 0]);
>> L
 
L = 
Revolute(std):  theta=q1   d=0           a=1           alpha=0           offset=0          
Revolute(std):  theta=q2   d=0           a=1           alpha=0           offset=0          

这个向量将被传递给构造函数 SerialLink：

>> two_link = SerialLink(L, 'name', 'two link')
 
two_link = 
 
two link:: 2 axis, RR, stdDH, slowRNE                            
+---+-----------+-----------+-----------+-----------+-----------+
| j |     theta |         d |         a |     alpha |    offset |
+---+-----------+-----------+-----------+-----------+-----------+
|  1|         q1|          0|          1|          0|          0|
|  2|         q2|          0|          1|          0|          0|
+---+-----------+-----------+-----------+-----------+-----------+

用以下指令，可以画出机器人的图形：

>> two_link.plot([0 0])
>> two_link.plot([pi/4 -pi/4])

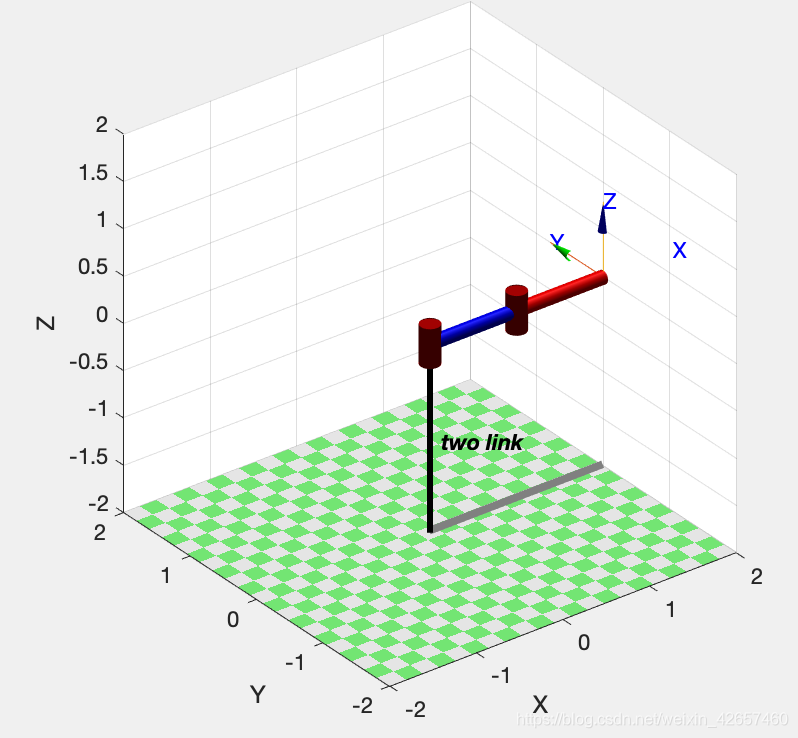
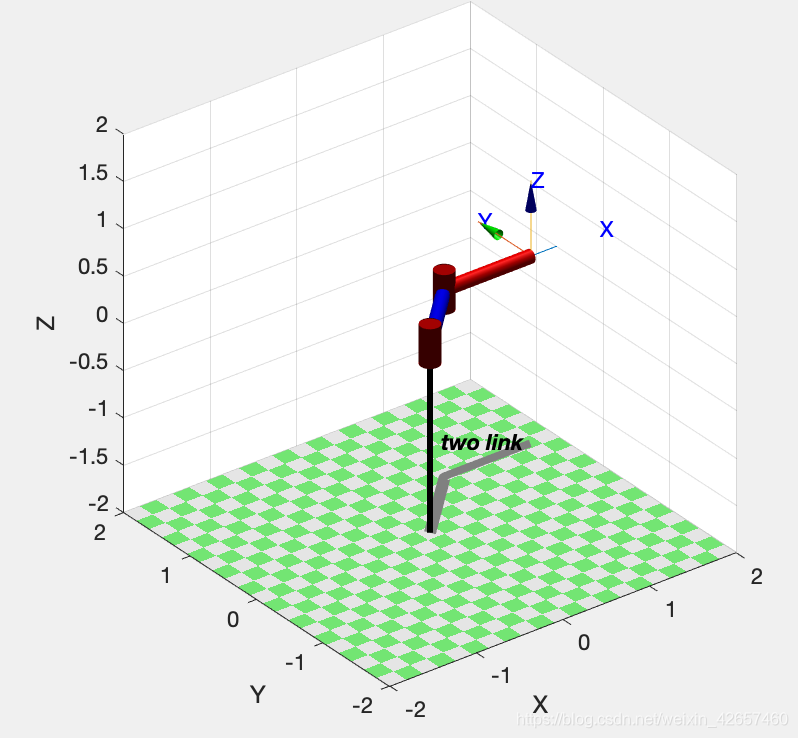
• 六轴机器人
  以 Puma 560 机器人为例，使用如下指令定义一个 Puma 560 机器人的实例（工具箱自带模板指令来定义很多常见的工业机器人），它将在工作区中创建一个名为 p560 的 SerialLink 对象：

>> mdl_puma560
>> p560
 
p560 = 
 
Puma 560 [Unimation]:: 6 axis, RRRRRR, stdDH, slowRNE            
 - viscous friction; params of 8/95;                             
+---+-----------+-----------+-----------+-----------+-----------+
| j |     theta |         d |         a |     alpha |    offset |
+---+-----------+-----------+-----------+-----------+-----------+
|  1|         q1|          0|          0|     1.5708|          0|
|  2|         q2|          0|     0.4318|          0|          0|
|  3|         q3|    0.15005|     0.0203|    -1.5708|          0|
|  4|         q4|     0.4318|          0|     1.5708|          0|
|  5|         q5|          0|          0|    -1.5708|          0|
|  6|         q6|          0|          0|          0|          0|
+---+-----------+-----------+-----------+-----------+-----------+  

>> p560.plot(qz)
>> p560.plot(qr)
>> p560.plot(qs)
>> p560.plot(qn)

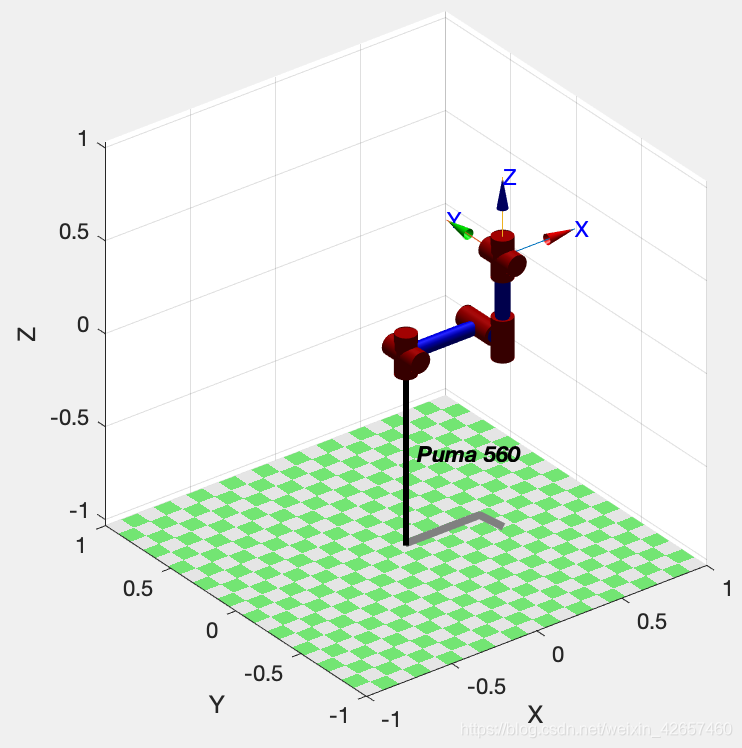
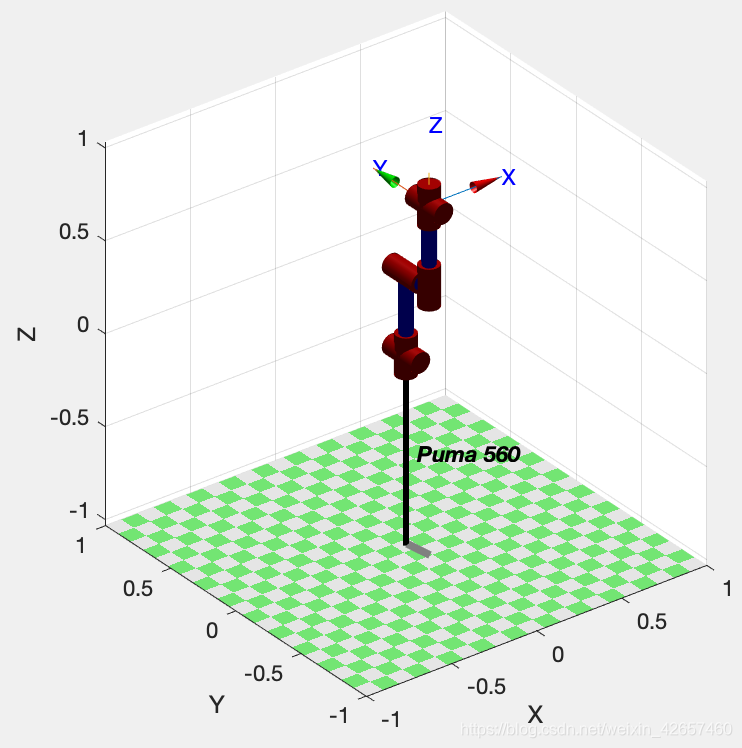
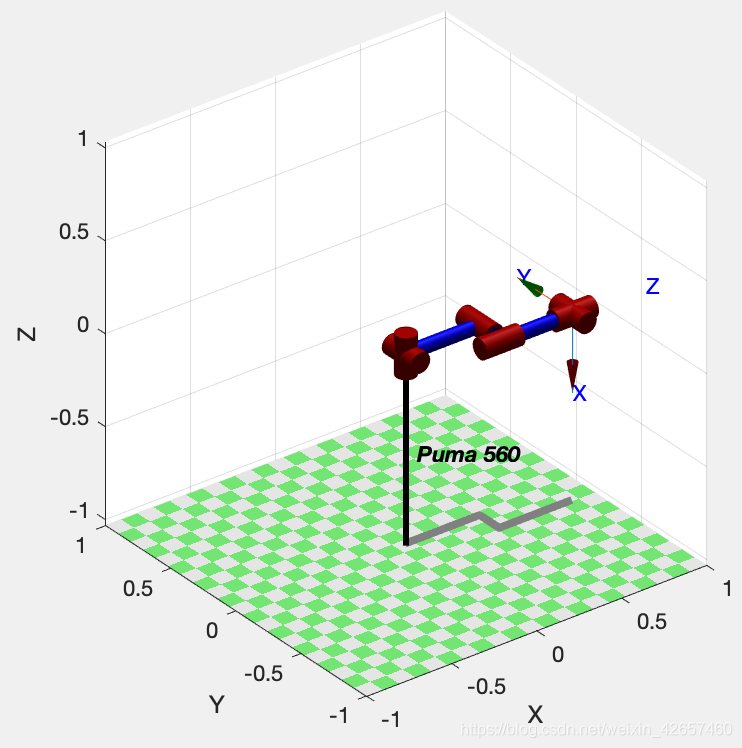
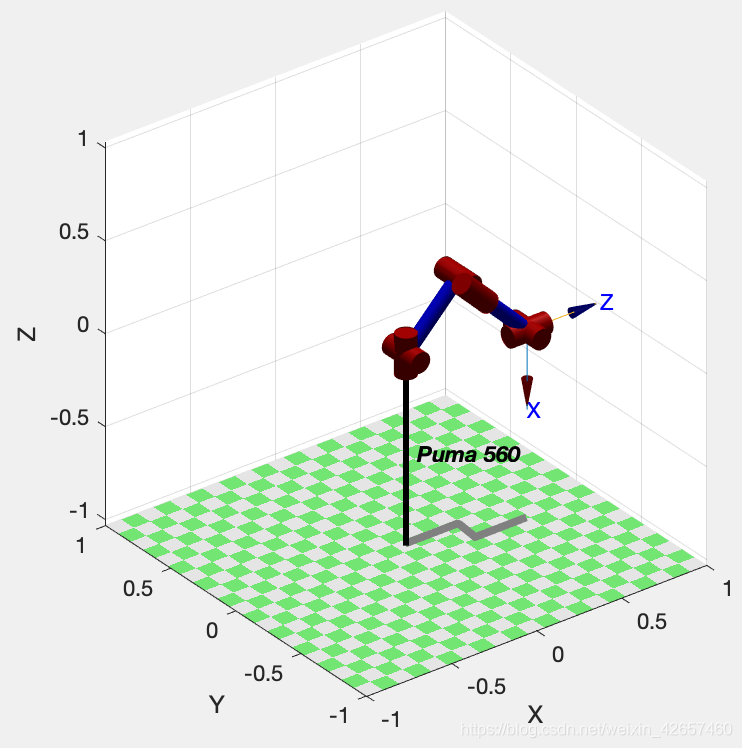
2.正运动学

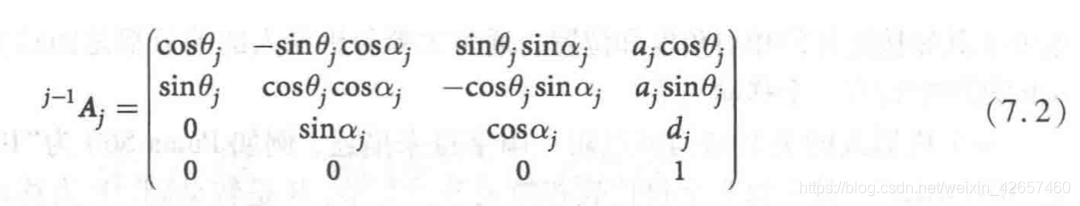
• 两连杆机器人 - planar2：

>> mdl_planar2 % 直接构造2连杆平面机器人，并创建名为 two_link 的 SerialLink 对象
>> two_link.fkine([0 0]) % q1 = 0, q2 = 0 时的变换矩阵
 

ans = 
         1         0         0         2
         0         1         0         0
         0         0         1         0
         0         0         0         1
>> two_link.fkine([pi/4 -pi/4]) % q1 = pi/4, q2 = -pi/4
 

ans = 
         1         0         0     1.707
         0         1         0    0.7071
         0         0         1         0
         0         0         0         1

• 六轴机器人 - Puma 560：

>> mdl_puma560 % 直接构造 Puma 560 机器人，并创建名为 P560 的 SerialLink 对象
>> p560.fkine(qz) % 零角度时的变换矩阵
 

ans = 
         1         0         0    0.4521
         0         1         0     -0.15
         0         0         1    0.4318
         0         0         0         1
>> p560.fkine(qn) % 标准状态时的变换矩阵
 

ans = 
         0         0         1    0.5963
         0         1         0   -0.1501
        -1         0         0  -0.01435
         0         0         0         1

3.逆运动学

给定期望的末端执行器位姿，求取所需的关节坐标。一般而言，逆运动学的解不是唯一的，而且对于某些类型的机械臂甚至没有封闭形式的解存在，只能求出一个数值解

• 封闭形式解 - ikine6s
  对于六轴机器人，其逆运动学具有封闭形式解的一个必要条件是：三个腕关节的轴相交于一个点。这意味着腕关节的运动只改变末端执行器的姿态，而不改变其位置

>> mdl_puma560
>> qn % 机器人标准状态的关节坐标

qn =

         0    0.7854    3.1416         0    0.7854         0

>> T = p560.fkine(qn) % 标准状态对应的末端执行器位姿
 

T = 
         0         0         1    0.5963
         0         1         0   -0.1501
        -1         0         0  -0.01435
         0         0         0         1
>> qi = p560.ikine6s(T) % ikine6s 方法计算其逆运动学的封闭解，要实现位姿 T，所需的关节坐标为 qi

qi =

    2.6486   -3.9270    0.0940    2.5326    0.9743    0.3734

由 qn 和 qi 的坐标比较可知，两组不同的关节坐标值得到了相同的末端执行器位姿，这两组坐标值对应的机器人位形如图所示：

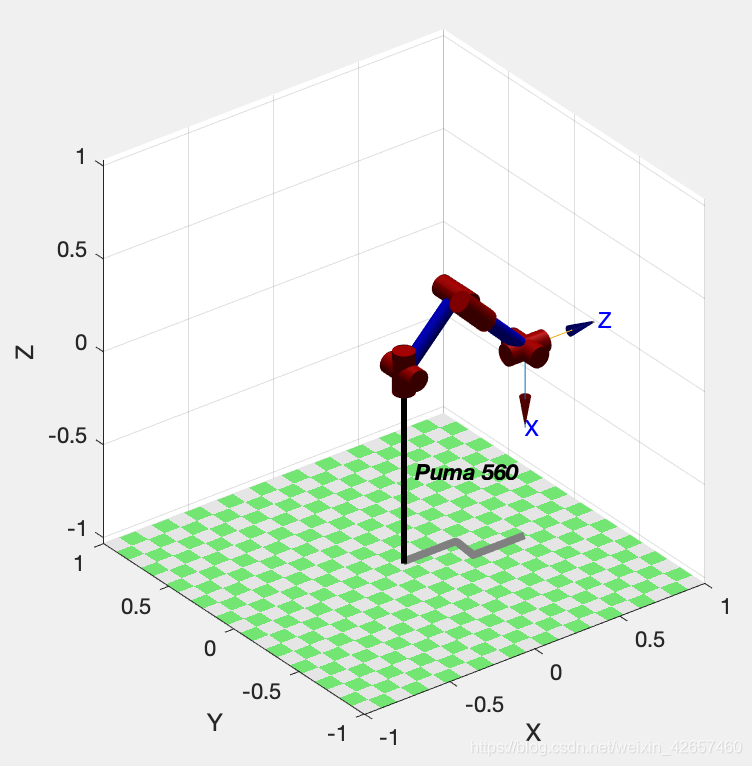
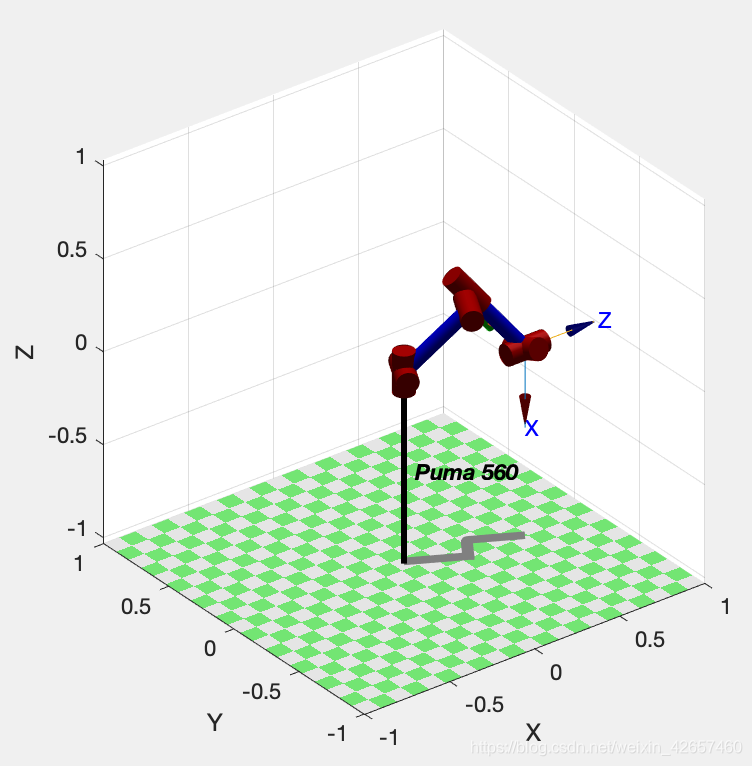
分别为左手运动学位形和右手运动学位形，一般来说，有8组不同的关节坐标值可以得到相同的末端执行器位姿

• 数值解 - ikine
  对于不具有6个关节和球形腕关节的机器人，需要使用一种迭代数值解，使用 ikine 方法来计算一般逆运动学解：

>> mdl_puma560
>> qn % 机器人标准状态的关节坐标

qn =

         0    0.7854    3.1416         0    0.7854         0

>> T = p560.fkine(qn) % 标准状态对应的末端执行器位姿
 

T = 
         0         0         1    0.5963
         0         1         0   -0.1501
        -1         0         0  -0.01435
         0         0         0         1
>> qi = p560.ikine(T) % ikine 方法计算其逆运动学的封闭解，要实现位姿 T，所需的关节坐标为 qi

qi =

   -0.0000   -0.8335    0.0940    0.0000   -0.8312   -0.0000

4.轨迹