算术运算符

需求分析
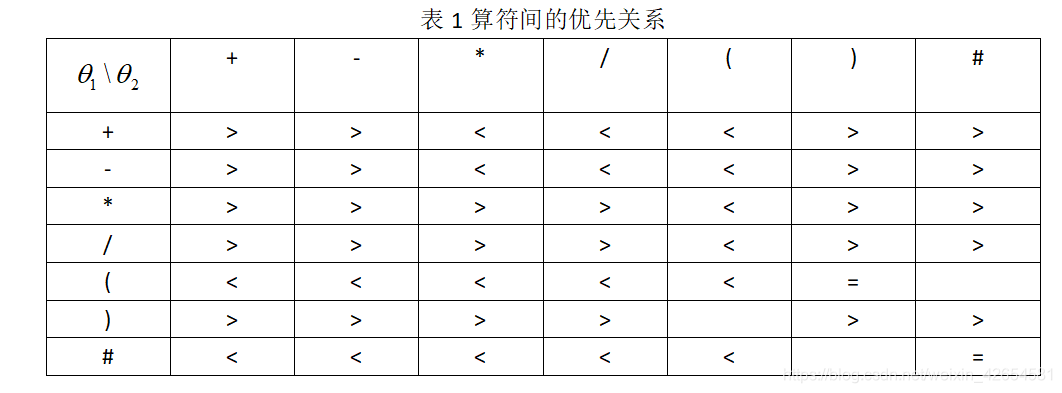
表达式求值的一种算法称为“算符优先法”，即定义算符之间的优先关系，在求解过程中，通过比较算符之间的优先关系，最终获得表达式的求解结果。
（1）以字符序列的形式从终端输入语法正确的、不含变量的任意位正浮点数表达式。
（2）根据表1给出的算符优先关系进行运算，且输入的算符只包含表中这7种。
（3）运算任意位正浮点数的算术四则混合运算表达式，得出结果并输出。

抽象数据类型
ADT Stack
{
数据对象：

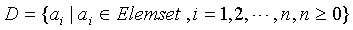
数据关系：

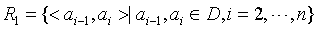
基本操作：
InitStack(&S)
操作结果：构造一个空栈S。
Push(&S,e)
初始条件：栈S存在
操作结果：插入元素e为新的栈顶元素。
Gettop(&S)
初始条件：栈S已存在并且非空
操作结果：用e返回栈顶元素。
Pop(&S,&e)
初始条件：栈S已存在并且非空
操作结果：删除S的栈顶元素，并用e返回其值。
EvaluateExpression()
操作结果：计算最终的结构并且返回其值。
}ADT Stack

ADT Arithmetic
{
数据对象：

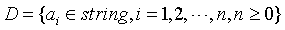
基本操作：
Zhuanhuan(a)
初始条件：a为字符串
操作结果：a转换为浮点数并返回。
In( c)
操作结果：判断字符c是否为符号。是返回TRUE，不是返回FALSE
Precede(a,b)
操作结果：比较a,b的优先顺序。返回”>””<”或”=”三种字符串。
Operate(a,theta,b)
操作结果：运算，其中a，b为数字，theta为符号。
EvaluateExpression()
操作结果：计算最终的结构并且返回其值。
}ADT Arithmetic

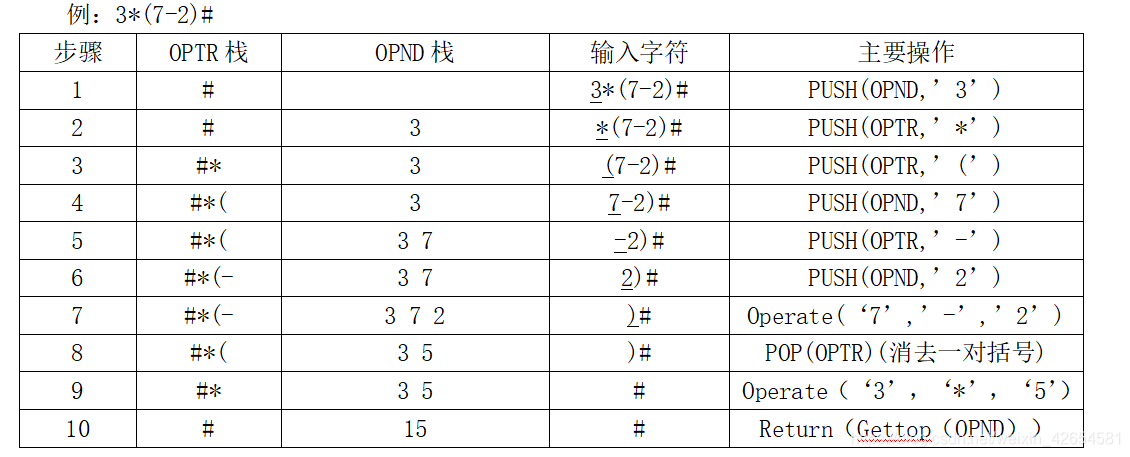
模拟运行过程

代码

#include<iostream>
#include<string>
#include <sstream>
#include<stdlib.h>
#pragma warning(disable:4996)
#define TRUE 1
#define FALSE 0
#define OVERFLOW -1
using namespace std;
typedef int Status;
typedef struct SNode {
	string data;
	struct SNode *next;
} SNode;
typedef struct node
{
	SNode* top;
	int count;
}*LinkStack;
//构造一个空栈
Status InitStack(LinkStack &S) {
	S = new node();
	S->top = NULL;
	S->count = 0;
	return TRUE;
}

//插入e
Status Push(LinkStack &S, string e) {
	SNode *p = new SNode();
	if (!p) {
		return OVERFLOW;
	}
	p->data = e;
	p->next = S->top;
	S->top = p;
	S->count++;
	return TRUE;
}

//用e返回S的栈元素
string GetTop(LinkStack &S) {
	if (!S)
		return 0;
	else
	{
		return S->top->data;
	}
}

//字符串转换为数字
float zhuanhuan(string a)
{
	stringstream b;
	float c;
	b << a;
	b >> c;
	return c;
}

//判断输入的字符是否是运算符
bool In(char c) {
	char fuhao[7] = { '+', '-', '*', '/', '(', ')', '#' };
	for (int i = 0; i < 7; i++) {
		if (c == fuhao[i]) {
			return true;
		}
	}
	return false;
}

//若栈不空，删除栈顶元素,用e返回其值
Status Pop(LinkStack &S, string &e) {
	SNode* p;
	if (!S)
		return FALSE;
	e = S->top->data;
	p = S->top;
	S->top = S->top->next;
	free(p);
	return TRUE;
}

//比较两个运算符的优先级
string Precede(string a, char b) {
	if ((a == "(" && b == ')') || (a == "#" && b == '#')) {
		return "=";
	}
	else if (((a=="+"||a=="-"||a=="("||a=="#")&&(b=='*'||b=='/'||b=='('))||(a=="("&&(b=='+'||b=='-'))||(a=="#"&&(b=='+'||b=='-'))||(a=="*"&&b=='(')) {
		return "<";
	}
	else
		return ">";
}

//运算a,b为数,theta为符号
string Operate(string a, string theta, string b) {
	float c,d;
	string r;
	stringstream aa;
	stringstream bb;
	stringstream result;
	aa << a;
	aa >> c;
	bb << b;
	bb >> d;
	if (theta == "+")
	{
		result << c + d;
		result >> r;
		return r;
	}
	if (theta == "-")
	{
		result << c - d;
		result >> r;
		return r;
	}
	if (theta == "*")
	{
		result << c * d;
		result >> r;
		return r;
	}
	if (theta == "/")
	{
		result << c / d;
		result >> r;
		return r;
	}
	return 0;
}

//算法3.4　表达式求值 p53页
string EvaluateExpression() {
	//算术表达式求值的算符优先算法，设OPTR和OPND分别为运算符栈和操作数栈
	//OP为运算符集合
	LinkStack OPTR, OPND;
	string c,x,theta,a,b,top,t,d;
	InitStack(OPTR); 
	InitStack(OPND);
	Push(OPTR, "#"); //将表达式起始符“#”压入OPTR栈
	cin >> c;
	for (int i = 0; i < c.length(); i++)
	{
		while (c[i] != '#' || (GetTop(OPTR) != "#")) //OPTR的栈顶元素不为“#”
		{
			if (!In(c[i])) 
			{//c不是运算符进OPND栈
				while (!In(c[i]))
				{
					t = t + c[i];
					i++;
				}
				Push(OPND, t);
				t = "";
			}
			else
			{
				string temp,m;
				m = GetTop(OPTR);
				temp = Precede(m,c[i]);
				if (temp == "<")//比较OPTR的栈顶元素和c[i]的优先级
				{
					d = d + c[i];
					Push(OPTR,d);
					i++;
					d = "";
				}
				if (temp == "=")
				{
					d = d + c[i];
					Pop(OPTR, d);
					i++;
					d = "";
				}
				if (temp == ">")
				{
					Pop(OPTR, theta);
					Pop(OPND, b);
					Pop(OPND, a);
					Push(OPND, Operate(a, theta, b));
				}
			}//else
		} //while
	}//for
	return GetTop(OPND); //OPND栈顶即为结果
}

int main() {
	do
	{
		int c;
		cout << "1.计算" << endl;
		cout << "2.退出" << endl;
		cout << "输入:";
		cin >> c;
		switch (c) 
		{
			case 1:
			{
				cout << "请输入不含变量的正浮点数算术表达式(以'#'结束)："<< endl;
				string res = EvaluateExpression();
				cout << "结果："<<zhuanhuan(res) << endl;
			}break;
		case 2:
		{
			cout << "退出" << endl;
			return 0;
		}
		default:
			break;
		}
		system("pause");
		system("cls");
	} while (1);
	return 0;
}

运行结果

实验不足
只能进行全体正浮点数的算术表达式运算，而不能对有表达式中含有负数的式子进行运算，若要改进为全体浮点数运算则需要将判断是否为符号位类型中的减号考虑多种情况。且灵活性较差，只能对表中存在的那些符号进行运算。若为负数中的负号则需要将其放入存储数值的栈中。但由于减号与负号在书写上是相同的符号，故实施还有待查询资料。

参考文献
1.《数据结构》 严蔚敏 吴伟民 清华大学出版社 2018年12月
2.https://blog.youkuaiyun.com/yh_zeng2/article/details/73441551 String字符串拼接应该使用哪种方式？ 曾燕辉
3.https://blog.youkuaiyun.com/sunshineacm/article/details/78068987 string和stringstream的用法 unshin
4.http://www.cplusplus.com/reference/sstream/stringstream/ stringstream
5.https://blog.youkuaiyun.com/believe_s/article/details/76473768 数据结构之链式栈的一些基本操作 believe_s