平衡二叉树（AVL）定义及其旋转

平衡二叉树（AVL）

平衡二叉树（AVL），是一个二叉排序树，同时任意节点左右两个子树的高度差（或平衡因子，简称BF）的绝对值不超过1，并且左右两个子树也满足。

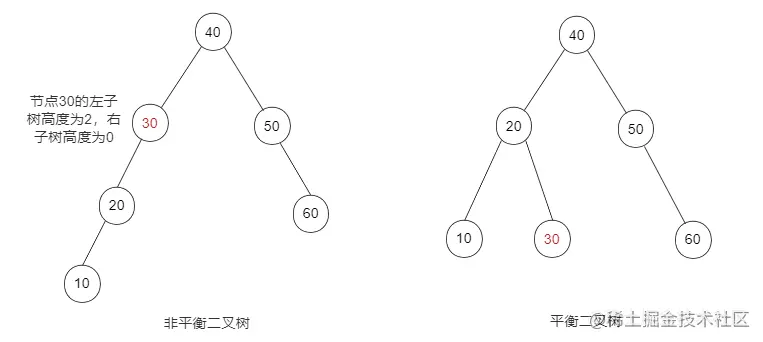
为什么使用平衡二叉树

通过二叉查找树的查找操作可以发现，一棵二叉查找树的查找效率取决于树的高度，如果使树的高度最低，那么树的查找效率也会变高。

如下面一个二叉树，全部由右子树构成

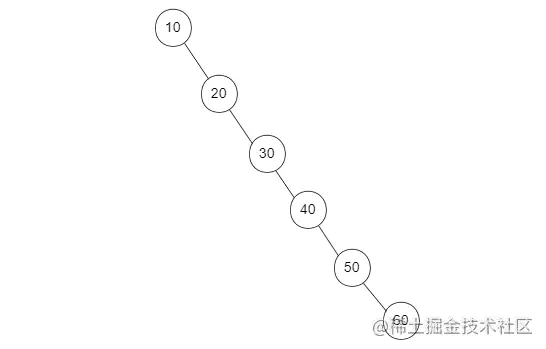
这个时候的二叉树其实就类似于链表，此时的查找时间复杂度为O(n)，而AVL树的查找时间复杂度为O(logn)。之前讲过O(logn)耗时是小于O(n)的，如下：

可参考：常见数据结构的时间复杂度

平衡二叉树的调整

一棵平衡二叉树的插入操作会有2个结果：

如果平衡没有被打破，即任意节点的BF=1，则不需要调整

如果平衡被打破，则需要通过旋转调整，且该节点为失衡节点

一棵失衡的二叉树通过以下调整可以重新达到平衡：

左旋：以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变

正在上传…重新上传取消

右旋：以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变

正在上传…重新上传取消

通过旋转最小失衡子树来实现失衡调整：

在一棵平衡二叉树新增节点，在新增的节点向上查找，第一个平衡因子的绝对值超过1（BF>1）的节点为根的子树称为最小不平衡子树。也就是说，一棵失衡的树，有可能多棵子树同时失衡，这时只需要调整最小的不平衡子树即可。

看完下面的旋转方式之后再回来看最小失衡子树旋转就很清晰了

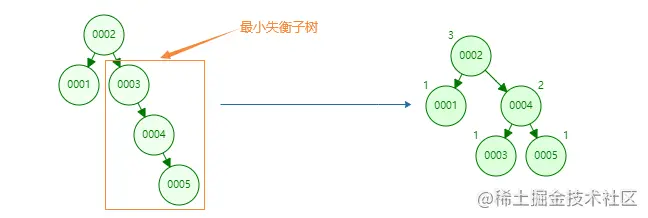
LL旋转

向左子树（L）的左孩子（L）插入新节点

插入节点在失衡节点的左子树的左边，经过一次右旋即可达到平衡，如下

• 插入新节点5，旧根节点40为失衡节点
• 旧根节点40为新根节点20的右子树
• 新根节点20的右子树30为旧根节点40的左子树

旋转过程

正在上传…重新上传取消

RR旋转

插入节点在失衡节点的右子树的右边，经过一次左旋即可达到平衡，如下

• 插入新节点60，旧根节点20为失衡节点
• 旧根节点20为新根节点40的左子树
• 新根节点40的左子树30为旧根节点20的右子树

旋转过程

LR旋转

插入节点在失衡节点的左子树的右边，先左旋，再右旋，如下

旋转过程

RL旋转

插入节点在失衡节点的右子树的左边，先右旋，再左旋，如下

旋转过程

代码实现

public class AVLTree {
    //节点
    public static class Node {
        int data; //数据
        Node leftChild; //左子节点
        Node rightChild;//右子节点
        int height; // 记录该节点所在的高度
​
        public Node(int data) {
            this.data = data;
        }
    }
    //获取节点的高度
    public static int getHeight(Node p){
        return p == null ? -1 : p.height; // 空树的高度为-1
    }
    public static void main(String[] args) {
        Node root = null;
        root = insert(root,40);
        root = insert(root,20);
        root = insert(root,50);
        root = insert(root,10);
        root = insert(root,30);
        //插入节点在失衡结点的左子树的左边
        root = insert(root,5);
        //打印树，按照先打印左子树，再打印右子树的方式
        printTree(root);
​
    }
​
    public static void printTree(Node root) {
        System.out.println(root.data);
        if(root.leftChild !=null){
            System.out.print("left:");
            printTree(root.leftChild);
        }
        if(root.rightChild !=null){
            System.out.print("right:");
            printTree(root.rightChild);
        }
    }
    // AVL树的插入方法
    public static Node insert(Node root, int data) {
        if (root == null) {
            root = new Node(data);
            return root;
        }
        if (data <= root.data) { // 插入到其左子树上
            root.leftChild = insert(root.leftChild, data);
            //平衡调整
            if (getHeight(root.leftChild) - getHeight(root.rightChild) > 1) {
                if (data <= root.leftChild.data) { // 插入节点在失衡结点的左子树的左边
                    System.out.println("LL旋转");
                    root = LLRotate(root); // LL旋转调整
                }else{ // 插入节点在失衡结点的左子树的右边
                    System.out.println("LR旋转");
                    root = LRRotate(root);
                }
            }
        }else{ // 插入到其右子树上
            root.rightChild = insert(root.rightChild, data);
            //平衡调整
            if(getHeight(root.rightChild) - getHeight(root.leftChild) > 1){
                if(data <= root.rightChild.data){//插入节点在失衡结点的右子树的左边
                    System.out.println("RL旋转");
                    root = RLRotate(root);
                }else{
                    System.out.println("RR旋转");//插入节点在失衡结点的右子树的右边
                    root = RRRotate(root);
                }
            }
        }
        //重新调整root节点的高度值
        root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1;
        return root;
    }
​
    /**
     * LR旋转
     */
    public static Node LRRotate(Node p){
        p.leftChild = RRRotate(p.leftChild); // 先将失衡点p的左子树进行RR旋转
        return LLRotate(p); // 再将失衡点p进行LL平衡旋转并返回新节点代替原失衡点p
​
    }
​
    /**
     * RL旋转
     */
    public static Node RLRotate(Node p){
        p.rightChild = LLRotate(p.rightChild); // 先将失衡点p的右子树进行LL平衡旋转
        return RRRotate(p); // 再将失衡点p进行RR平衡旋转并返回新节点代替原失衡点p
    }
​
    /*
     * LL旋转
     * 右旋示意图(对结点20进行右旋)
     *      40                       20
     *     /  \                     /  \
     *    20  50                  10   40
     *   /  \        LL旋转       /    / \
     *  10  30                  5    30  50
     *  /
     * 5
     */
    public static Node LLRotate(Node p){ // 40为失衡点
        Node lsubtree = p.leftChild;   //失衡点的左子树的根结点20作为新的结点
        p.leftChild = lsubtree.rightChild; //将新节点的右子树30成为失衡点40的左子树
        lsubtree.rightChild = p; // 将失衡点40作为新结点的右子树
        // 重新设置失衡点40和新节点20的高度
        p.height = Math.max(getHeight(p.leftChild), getHeight(p.rightChild)) + 1;
        lsubtree.height = Math.max(getHeight(lsubtree.leftChild), p.height) + 1;
        return lsubtree; // 新的根节点取代原失衡点的位置
    }
    /*
     * RR旋转
     * 左旋示意图(对结点20进行左旋)
     *      20                          40
     *     /  \                        /  \
     *    10  40                     20   50
     *       /  \      RR旋转        / \    \
     *      30  50                 10 30   60
     *           \
     *           60
     */
    public static Node RRRotate(Node p){ // 20为失衡点
        Node rsubtree = p.rightChild;  //失衡点的右子树的根结点40作为新的结点
        p.rightChild = rsubtree.leftChild; //将新节点的左子树30成为失衡点20的右子树
        rsubtree.leftChild = p; // 将失衡点20作为新结点的左子树
        // 重新设置失衡点20和新节点40的高度
        p.height = Math.max(getHeight(p.leftChild), getHeight(p.rightChild)) + 1;
        rsubtree.height = Math.max(getHeight(rsubtree.leftChild), getHeight(rsubtree.rightChild)) + 1;
        return rsubtree; // 新的根节点取代原失衡点的位置
    }
}
​
复制代码

 文档出处：

有图有真相！平衡二叉树AVL实现 - 掘金