一道十分有趣的概率题！3局2胜和5局3胜哪个胜算更大？你怎么思考

今天看到一个关于概率学的题目，感觉挺不错的，于是自己研究了一下！

题目为：“5局3胜和3局2胜，哪种胜算大”

我看了一下网友的评论，有一些人直接通过简单计算，3除以5，2除以3来进行比较。也有人从侧面分析：五局三胜靠实力，三局两胜靠运气的成分更大些！

/*这里有我自己整理了一套最新的python系统学习教程，
包括从基础的python脚本到web开发、爬虫、数据分析、
数据可视化、机器学习等。小编这里推荐加小编的python学习群：895,817, 687

我们自己来用程序来算一下

设我单局胜率为p，p=0.5的话，显然无论哪种决胜方式都是50%胜算。

不妨p>0.5。很容易给出，3局2胜，胜算为：

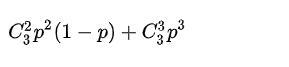
若5局3胜，胜算为:

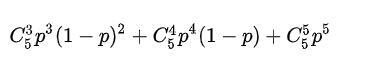
编程计算结果：

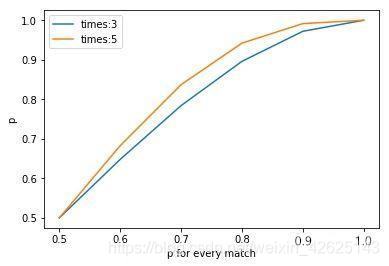
横坐标为单局比赛胜率，纵坐标为特定决胜方式的胜算。

这里p分别取了0.5—1之间均匀的6个点。

可以看到，0.5<p<1时，5局3胜的胜算一直大于3局2胜。

那么如果是更多局呢？比如7局4胜，9局5胜，11局6胜？

结果如下：

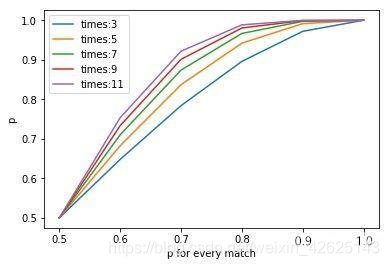
而“一局定胜负”的胜算，显然就是从(0.5，0.5)到(1，1)对角线。

所以可以得出结论，对水平高的一方，采用局数越多的决胜方式，胜算越大。

反过来也可以说，局数越多的决胜方式，越能公正地比较出选手之间的差异。因为随着比赛局数的增加，“单局胜率低(也就是水平较弱)的那个，越来越难获得最终的胜利了”。

——————————————————————————————————

有些人对我给出胜算的公式存疑，说5局3胜赢了3局就不用再打了。这里解释下：

是的，5局3胜，赢了3局后面就不用比了。但是我让他继续打完这5场，并不会影响胜负结果。这样可以方便计算。这是数学竞赛中会用的一个小技巧。

——————————————————————————————————

已有2位朋友给出了数学上的严格证明：

1.直接证明2n+1局胜算高于2n-1局.

设2n-1局胜算为q

2n-1局恰好赢了n局的概率为

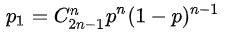
2n-1局恰好赢了n-1局的概率为

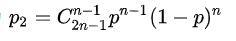
则 q-p1为2n-1局里至少赢n+1局的概率。

考虑2n+1局的前2n-1局，

如果这2n-1局至少赢n+1局，则无论后面结果如何，都是胜利。

如果这2n-1局赢了n局，则需要后两场至少赢一局。

如果这2n-1局赢了n-1局，则需要后两场都赢。

因此2n+1局的胜算为：

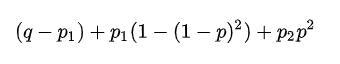
要证明这个大于q.

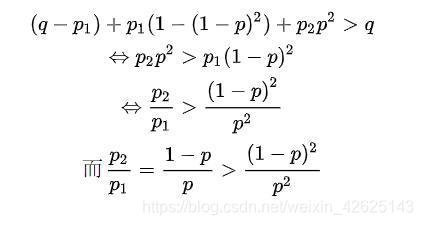
因此结论成立。

2.通过概率论知识来分析。

总而言之，言而总之，我也深知这对统计专业的人来说确实是很基础的问题。不过有理论计算，有程序，有初等数学的严格证明，都可以让原先对这个问题不那么确定的人从此有了足够的底气来确信哪种“决胜模式”更适合他们。