Java实现零钱找零算法项目实战

本文还有配套的精品资源，点击获取

简介：在Java编程中，找零钱问题是一个广泛应用的算法问题。本文将深入探讨这一问题，并提供动态规划与贪心算法两种解决方案，以及在Java中的代码实现。找零问题要求我们用最少数量的硬币组合凑出目标金额。我们通过创建数组来追踪凑出每个金额所需的最少硬币数，并采用贪心策略来选取面值最大的硬币。在实际应用中，此问题常见于电商退款处理、游戏货币兑换等场景。掌握解决此问题的算法对于Java开发者至关重要。

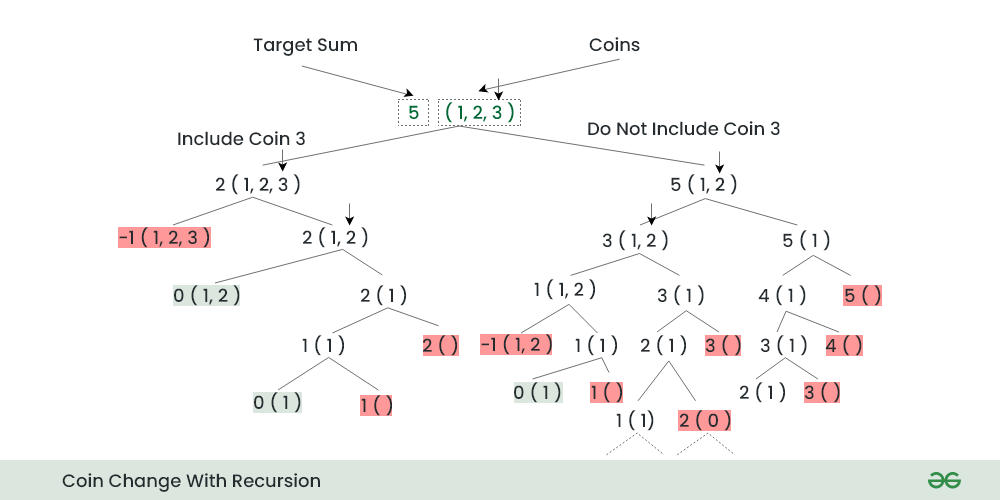
1. 找零问题描述与算法应用

1.1 找零问题简介

找零问题是计算机科学中经典的问题之一，尤其在零售业与金融交易处理中极为常见。问题的核心是给定货币面额的集合，如何用最少的硬币或纸币数量组成顾客应得的找零金额。这不仅涉及到货币价值计算，还关系到资源优化配置。

1.2 找零问题的实际应用场景

在现实生活中，找零问题有着广泛的应用。例如，在超市结算台、银行货币兑换、甚至是现代的电子支付场景中，后台系统都需要处理找零逻辑，保证交易的顺利进行。一个高效的找零算法不仅能够提高工作效率，还能提升顾客的购物体验。

1.3 算法在找零问题中的应用

为了解决找零问题，不同的算法策略如动态规划和贪心算法被提出和应用。本章将深入探讨这些算法的原理、实现和在找零问题上的具体应用。通过分析这些算法，我们可以理解其背后的设计思想以及在实际问题中如何进行选择和优化。

接下来的内容将继续深入探讨动态规划算法，并展示其在找零问题上的实际应用和分析。

2. 动态规划算法实现

2.1 动态规划基本原理

动态规划是一种解决问题的数学方法，它将复杂问题分解为简单子问题，通过解决子问题来构建复杂问题的解决方案。不同于简单的自顶向下或自底向上的递归方法，动态规划存储已解决的子问题的解，避免重复计算，这使得它在处理具有重叠子问题和最优子结构性质的问题时特别有效。

2.1.1 动态规划定义及其解决问题的特点

动态规划（Dynamic Programming，DP）通常用于优化问题，其目标是在给定的约束条件下找到最优解。它要求问题可以被分解为重叠的子问题，并且这些子问题的解决方案可以组合起来解决原问题。

动态规划解决问题的关键特点包括：

• 最优子结构 ：问题的最优解包含其子问题的最优解。
• 重叠子问题 ：在递归计算过程中，相同的小问题会被多次计算。
• 无后效性 ：解决问题的中间过程不会影响最终结果，即问题的后期状态只依赖于早期状态和决策。

动态规划通常采用自底向上的方法，从最小子问题开始逐步构建出问题的解。

2.1.2 动态规划与贪心算法、分治算法的比较

贪心算法和分治算法是另外两种常见的算法范式。它们与动态规划有相似之处，但也存在本质的区别。

• 贪心算法 ：在每一步都选择当前看来最好的选择，不考虑全局最优，因此并不保证能够得到全局最优解。
• 分治算法 ：将问题分解为独立的子问题，递归地解决这些子问题，然后合并结果得到原问题的解。它适合于子问题完全独立的情况。
• 动态规划 ：解决子问题时考虑重叠子问题，通过存储已解决的子问题的解来优化性能。它通常用于子问题不完全独立时的情况。

动态规划的核心在于利用中间结果来避免重复计算，而贪心算法则不具备这样的机制，分治算法则是在子问题之间没有重叠时最为高效。

2.2 动态规划求解找零问题

找零问题是一个经典的优化问题，可以用动态规划算法高效求解。该问题可以通过数学建模转化为动态规划问题，然后按照动态规划的步骤来解决。

2.2.1 找零问题的数学建模

假设我们有一堆硬币，每种硬币的面额不同，我们要给出一定数额的找零。问题的目标是找出硬币组合的数量，使得给出的硬币数最少。

数学建模过程如下：

1. 定义状态： dp[i] 表示给出总额为 i 的找零所需的最少硬币数。
2. 状态转移方程： dp[i] = min(dp[i], dp[i - coin] + 1) ，其中 coin 是当前考虑的硬币面额， i - coin >= 0 。
3. 初始化： dp[0] = 0 （给出总额为0的找零不需要任何硬币），其余 dp[i] 初始值设为一个足够大的数，表示无解。

2.2.2 动态规划算法的步骤和示例

动态规划算法求解找零问题通常遵循以下步骤：

1. 确定状态和状态表示：如上述数学建模所定义。
2. 确定初始条件和边界情况：如上述初始化。
3. 状态转移方程的确定：如上述状态转移方程。
4. 根据状态转移方程计算最终的状态值。

接下来给出一个简单的示例：

假设我们有面额为1、3、4的硬币，现在需要给出总额为6的找零。使用动态规划，我们首先初始化 dp[0] = 0 ，然后对每一种可能的总额进行迭代计算：

for i in range(1, 7):  # 总额从1到6
    for coin in [1, 3, 4]:  # 可用硬币面额
        if i - coin >= 0:
            dp[i] = min(dp[i], dp[i - coin] + 1)

通过上述步骤，我们最终得到 dp[6] 的值即为最少硬币数量。

2.2.3 动态规划算法的时间复杂度分析

时间复杂度主要取决于状态数量和状态转移方程的计算复杂度。对于找零问题，状态的数量与总额的最大值成正比，假设最大值为 m ，硬币种类数为 n ，则时间复杂度为 O(m*n) 。由于每个状态只计算一次，空间复杂度为 O(m) ，用于存储每个状态的值。

graph TD
A[开始] --> B[初始化dp数组]
B --> C{遍历总额}
C -->|i = 1| D[遍历硬币种类]
D -->|coin = 1| E[计算dp[i]]
E -->|coin = 3| E
E -->|coin = 4| E
D -->|遍历结束| C
C -->|i = 6| C
C --> F[输出dp[m]]

通过这个流程图，我们可以更清晰地看到动态规划算法解决问题的步骤。

3. 贪心算法实现

3.1 贪心算法的基本原理

3.1.1 贪心算法定义及其适用场景

贪心算法（Greedy Algorithm）是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。贪心算法并不保证会得到最优解，但是在某些问题中贪心策略能够得到全局最优解。

贪心算法通常用于求解最优化问题，特别是在满足某个优化条件时，贪心策略能够迅速得到局部最优解。它适用于具有“贪心选择性质”的问题，也就是说，一个问题的整体最优解可以通过一系列局部最优的选择得到。贪心算法的一个关键点是：局部最优解能决定全局最优解。

3.1.2 贪心算法的策略和局限性

贪心算法的策略主要是在每一步决策中，都选取当前情况下的最优解，但不考虑这些选择对未来的可能影响。贪心算法的局限性在于它不能保证得到全局最优解，因为它不回溯（没有回溯过程来检查之前的决策是否合理）。尽管如此，在某些情况下，贪心算法能够提供一个相对较好的解决方案。

一个典型的贪心算法示例是在硬币找零问题中的应用。例如，在美国使用面值为1, 5, 10, 25美分的硬币，给定一个要找零的总金额，使用最少硬币数量的贪心算法策略是每次都尽量使用面值最大的硬币。

3.2 贪心算法求解找零问题

3.2.1 贪心算法在找零问题中的应用

假设我们需要找给顾客14美分的零钱，使用贪心算法，我们按照以下步骤进行：

1. 从最大的硬币开始，即面值为25美分的硬币。
2. 25美分大于14美分，所以不使用25美分的硬币。
3. 接下来是10美分，14 - 10 = 4美分，我们还剩4美分。
4. 然后是5美分，但5美分大于剩余的4美分，所以不使用5美分的硬币。
5. 最后我们使用4个1美分的硬币，得到总共14美分。

3.2.2 贪心算法与动态规划算法的对比分析

贪心算法和动态规划算法在找零问题中的对比分析如下：

• 时间复杂度 ：贪心算法具有更优的时间复杂度，因为它不需要像动态规划那样存储中间状态，每一步的计算都是独立的。
• 空间复杂度 ：由于贪心算法不需要存储中间状态，它的空间复杂度通常低于动态规划。
• 适用性 ：对于找零问题这种具有贪心选择性质的问题，贪心算法是适用的。但对于需要全局最优解的问题，比如某些旅行商问题（TSP）的变体，贪心算法就无能为力了。
• 正确性 ：在找零问题中，贪心算法可以保证得到最优解。但在其他问题中，贪心算法可能只能得到局部最优解。

3.2.3 贪心算法在不同场景下的调整与优化

贪心算法的优化通常依赖于问题本身和贪心策略的选择。在一些场景中，通过调整贪心策略来获得更好的结果是可能的。例如，在找零问题中，如果硬币的面值不是标准的1, 5, 10, 25美分，而是有其他特殊面值（例如41美分），那么简单的贪心策略可能就不会给出最优解。在这种情况下，可能需要根据硬币的特殊组合来调整贪心选择标准。

下面是一个简单的Java代码示例，用来展示贪心算法在找零问题上的应用：

public class GreedyChangeMaking {

    // 计算需要的硬币数量
    public static int[] getCoins(int[] denominations, int amount) {
        int[] coinCount = new int[denominations.length];
        for (int i = denominations.length - 1; i >= 0; i--) {
            while (amount >= denominations[i]) {
                amount -= denominations[i];
                coinCount[i]++;
            }
        }
        return coinCount;
    }

    public static void main(String[] args) {
        int[] denominations = {1, 5, 10, 25}; // 硬币面值
        int amount = 41; // 找零金额
        int[] coinCount = getCoins(denominations, amount);
        System.out.println("Coin count for amount " + amount + " cents:");
        for (int i = 0; i < denominations.length; i++) {
            System.out.println(denominations[i] + " cent coin count: " + coinCount[i]);
        }
    }
}

在上面的代码中，我们定义了一个 getCoins 方法，它接受硬币面值数组 denominations 和需要找零的金额 amount 。然后，它使用贪心算法来计算每种面值硬币的所需数量，并打印出来。通过这种方式，我们可以看到贪心算法在实际中的应用，以及它在找零问题上的效率和准确性。

4. Java代码实现与项目实战

4.1 Java环境准备与工具使用

4.1.1 Java开发环境的搭建

为了开展Java代码的实现和项目实战，首先需要搭建一个适合开发的Java环境。这通常包括安装Java开发工具包（JDK）以及配置相应的环境变量。具体步骤如下：

1. 下载JDK : 访问Oracle官网或其他JDK提供商的网站下载最新版本的JDK。目前OpenJDK是开源社区广泛使用的选择。

2. 安装JDK : 依据不同的操作系统，进行安装。以Windows为例，下载可执行安装文件，双击运行并遵循向导提示完成安装。

3. 配置环境变量 :
   - JAVA_HOME ：指向JDK的安装目录。
   - PATH ：添加 %JAVA_HOME%\bin ，确保可以全局访问Java命令。
   - CLASSPATH ：添加 .;%JAVA_HOME%\lib\dt.jar;%JAVA_HOME%\lib\tools.jar; ，为Java类加载器指定路径。

4. 验证安装 : 打开命令提示符，输入 java -version 和 javac -version ，如果显示安装的JDK版本，说明环境配置成功。

4.1.2 必要的开发工具介绍（IDE, 版本控制工具等）

在Java开发中，有一系列的工具可以帮助我们提高开发效率和项目管理质量，以下是一些推荐的工具：

1. 集成开发环境（IDE） :
   - IntelliJ IDEA ：拥有智能的编码辅助功能，强大的插件生态系统。
   - Eclipse ：广泛使用的老牌IDE，具有众多插件支持。
   - NetBeans ：由Oracle提供的免费开源IDE，适合快速开发。

2. 版本控制工具 :
   - Git : 分布式版本控制系统，适合团队协作和代码管理。
   - GitHub : 提供Git仓库托管服务，是全球最大的代码共享平台。
   - GitLab 或 Bitbucket ：提供了与GitHub类似的代码托管服务。

3. 构建工具 :
   - Maven ：项目管理和构建自动化工具，对Java项目有很好的支持。
   - Gradle ：一个基于Apache Ant和Apache Maven概念的项目自动化构建工具。

4. 代码质量检查工具 :
   - Checkstyle : 帮助开发者编写符合编码规范的Java代码。
   - FindBugs : 检测Java代码中可能的bug。

4.2 动态规划算法的Java实现

4.2.1 动态规划算法的Java代码框架设计

在Java中实现动态规划算法，首先需要设计一个合理的代码框架。这里以找零问题为例，说明动态规划的代码框架设计。

public class ChangeMaking {

    // 方法计算找零问题的最小硬币数量
    public int findMinimumCoins(int[] denominations, int amount) {
        // dp[i] 表示组成金额i所需的最小硬币数量
        int[] dp = new int[amount + 1];
        // 初始化dp数组，最大可能值设置为一个很大的数（或金额+1）
        Arrays.fill(dp, amount + 1);
        // 金额为0时，不需要硬币
        dp[0] = 0;

        // 遍历所有金额，从1到amount
        for (int i = 1; i <= amount; i++) {
            // 遍历所有面额
            for (int coin : denominations) {
                // 如果当前面额小于等于当前金额
                if (i >= coin) {
                    // 更新dp[i]
                    dp[i] = Math.min(dp[i], dp[i - coin] + 1);
                }
            }
        }

        // 如果dp[amount]未被更新过，返回-1表示没有解
        return dp[amount] > amount ? -1 : dp[amount];
    }
}

4.2.2 动态规划算法的具体编码实现

在框架设计完成后，我们就可以根据具体问题的需要填充代码逻辑。以下是实现找零问题的动态规划算法的完整Java代码：

import java.util.Arrays;

public class ChangeMaking {

    public int findMinimumCoins(int[] denominations, int amount) {
        // 确保面额数组按降序排列
        Arrays.sort(denominations);
        int[] dp = new int[amount + 1];
        // 初始值设为最大，表示无法构成
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0; // 金额为0时不需要硬币

        for (int i = 1; i <= amount; i++) {
            for (int coin : denominations) {
                if (i >= coin) {
                    if (dp[i - coin] != Integer.MAX_VALUE) {
                        dp[i] = Math.min(dp[i], dp[i - coin] + 1);
                    }
                } else {
                    break; // 由于数组是降序的，后面的值只会更大，所以可以直接终止
                }
            }
        }

        // 如果dp[amount]仍然为初始最大值，表示无法构成
        return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];
    }

    public static void main(String[] args) {
        ChangeMaking cm = new ChangeMaking();
        int[] denominations = {1, 2, 5}; // 硬币面额
        int amount = 11; // 需要找零的金额
        System.out.println("Minimum coins required: " + cm.findMinimumCoins(denominations, amount));
    }
}

这段代码实现了找零问题的动态规划解决方案。它首先初始化一个数组 dp ，其中 dp[i] 表示组成金额 i 所需要的最小硬币数量。然后通过迭代的方式计算每一个 dp[i] 的值，最终返回能够组成总金额所需的最小硬币数量。

4.3 贪心算法的Java实现

4.3.1 贪心算法的Java代码框架设计

贪心算法与动态规划不同，它在每一步选择中都采取当前状态最好或最优的选择，以期望导致结果是最好或最优的算法。以下是贪心算法的Java代码框架设计：

public class GreedyChangeMaking {

    // 方法计算找零问题的最小硬币数量
    public int findMinimumCoins(int[] denominations, int amount) {
        // 由于贪心算法要求面额从大到小排序，所以这里再次进行排序
        Arrays.sort(denominations);
        int numCoins = 0;
        for (int i = denominations.length - 1; i >= 0; i--) {
            // 循环使用最大的硬币面额
            while (amount >= denominations[i]) {
                amount -= denominations[i];
                numCoins++;
            }
            // 如果已经找完零钱，跳出循环
            if (amount == 0) break;
        }
        return amount == 0 ? numCoins : -1;
    }
}

4.3.2 贪心算法的具体编码实现

完成了贪心算法的框架设计，现在我们来实现具体的代码：

import java.util.Arrays;

public class GreedyChangeMaking {

    public int findMinimumCoins(int[] denominations, int amount) {
        // 对面额数组进行降序排序
        Arrays.sort(denominations);
        int numCoins = 0;
        int i = denominations.length - 1;

        while (amount > 0 && i >= 0) {
            // 尽可能多地使用当前面额的硬币
            while (amount >= denominations[i]) {
                amount -= denominations[i];
                numCoins++;
            }
            i--; // 考虑下一个较小的面额
        }

        // 如果最终找完零钱，返回硬币数量；否则返回-1表示没有解决方案
        return amount == 0 ? numCoins : -1;
    }

    public static void main(String[] args) {
        GreedyChangeMaking gcm = new GreedyChangeMaking();
        int[] denominations = {1, 2, 5}; // 硬币面额
        int amount = 11; // 需要找零的金额
        System.out.println("Minimum coins required: " + gcm.findMinimumCoins(denominations, amount));
    }
}

4.4 项目实战：找零系统开发

4.4.1 系统需求分析与设计

找零系统的开发需求如下：

• 功能需求 ：系统需要能够接受用户输入的金额和可用硬币面额，并输出最小硬币组合。
• 性能需求 ：系统需要高效地处理输入，并快速给出结果。
• 用户界面 ：提供简洁的命令行界面供用户输入和查看结果。

在设计上，我们将系统分为以下模块：

• 输入模块 ：接收用户输入的金额和硬币面额。
• 计算模块 ：使用动态规划或贪心算法计算找零问题的最小硬币组合。
• 输出模块 ：显示计算结果给用户。

4.4.2 功能模块划分与编码实现

接下来，我们根据设计来实现找零系统的功能模块：

// ChangeMakingSystem.java
public class ChangeMakingSystem {

    private ChangeMaking dynamicChange;
    private GreedyChangeMaking greedyChange;

    public ChangeMakingSystem() {
        dynamicChange = new ChangeMaking();
        greedyChange = new GreedyChangeMaking();
    }

    public void execute() {
        System.out.println("Welcome to the Change Making System");
        int[] denominations = new int[0];
        int amount = 0;

        // 输入处理
        System.out.print("Enter available denominations separated by space: ");
        String[] denominationInput = ConsoleUtils.getUserInput().split(" ");
        denominations = Arrays.stream(denominationInput).mapToInt(Integer::parseInt).toArray();

        System.out.print("Enter the amount you want to make change for: ");
        amount = Integer.parseInt(ConsoleUtils.getUserInput());

        // 动态规划实现
        int dynamicResult = dynamicChange.findMinimumCoins(denominations, amount);
        System.out.println("Dynamic Programming approach:");
        if (dynamicResult == -1) {
            System.out.println("No solution.");
        } else {
            System.out.println("Minimum coins required: " + dynamicResult);
        }

        // 贪心算法实现
        int greedyResult = greedyChange.findMinimumCoins(denominations, amount);
        System.out.println("Greedy approach:");
        if (greedyResult == -1) {
            System.out.println("No solution.");
        } else {
            System.out.println("Minimum coins required: " + greedyResult);
        }
    }

    public static void main(String[] args) {
        new ChangeMakingSystem().execute();
    }
}

// ConsoleUtils.java
public class ConsoleUtils {
    public static String getUserInput() {
        Scanner scanner = new Scanner(System.in);
        return scanner.nextLine();
    }
}

4.4.3 系统测试与性能评估

在完成编码后，需要对找零系统进行系统测试与性能评估。主要的测试目标如下：

1. 功能性测试 ：确保系统能够正确处理各种输入，包括边界情况。
2. 性能测试 ：通过大量的输入测试算法的执行时间和内存消耗。

为了进行测试，可以编写一系列的测试用例，包括：

• 正常用例 ：期望得到正确结果的常规输入。
• 边界用例 ：如输入面额中包含0，或找零金额为0的情况。
• 异常用例 ：如输入非法金额或面额，输入的面额无法组成金额等。

在实际部署之前，使用这些测试用例对系统进行全面测试，并记录性能指标以评估系统的实际运行效率。

通过以上步骤，找零系统就可以开发完成，并准备用于实际应用中。接下来的章节，我们将探讨找零问题在实际应用中的重要性和未来的创新方向。

5. 找零问题在实际应用中的重要性

5.1 找零问题在商业领域的影响

在零售业，找零一直是一个需要快速且准确处理的环节。如何在保持高效率的同时确保顾客满意度，是一个需要细致考虑的问题。找零问题的自动化和效率优化对整个商业领域有深远影响。

5.1.1 零售业找零的自动化与效率

随着技术的发展，自动化找零系统逐渐取代了人工找零的方式。这不仅提高了结账的速度，也减少了人为错误的发生。例如，自动找零机可以在几秒钟内完成找零，同时还能提供小票、计数等附加功能。这在高峰期尤其重要，能够有效减少顾客的等待时间，提升购物体验。

5.1.2 电子支付中的找零算法优化

在电子支付大行其道的今天，找零算法依然扮演着重要角色。例如，在线上购物时，虽然不需要物理的零钱，但系统在计算折扣、优惠、税费时，依旧需要应用找零算法。优化这些算法可以减少交易处理时间，提升系统性能，间接影响到用户体验。

5.2 找零问题在技术领域的研究价值

找零问题在技术层面，特别是算法优化领域，提供了挑战和机会。随着数据量的不断增长，处理大规模找零问题成为计算能力的试金石。

5.2.1 算法优化对计算能力的挑战

在设计找零算法时，通常需要在时间复杂度和空间复杂度之间做出平衡。例如，动态规划算法在解决找零问题时需要存储中间结果，而贪心算法则在某些情况下不需要。随着问题规模的增大，对计算能力的要求也随之上升，这就要求算法工程师不断地优化算法以适应更大的数据集。

5.2.2 找零问题在大数据处理中的应用前景

在大数据时代，找零问题的处理变得更加复杂和多样化。例如，处理海量交易记录，优化金融结算系统，或者在网络交易中实现实时找零计算等。在这些场景中，找零算法的研究和应用能够帮助公司更有效地管理资金流，降低成本，提高安全性。

5.3 未来展望与创新方向

随着技术的不断进步，找零问题的解决方法也在不断演进。对于未来，我们可以期待在找零问题上的创新与突破。

5.3.1 找零问题与人工智能结合的可能性

人工智能的发展为找零问题带来了新的解决方案。例如，通过机器学习预测顾客的支付习惯，优化找零库存管理；或者利用深度学习技术识别假币，防止欺诈行为。这些创新将使得找零过程更加智能化，安全可靠。

5.3.2 探索新的算法模型以解决更复杂的找零问题

随着商业环境的多样化和复杂化，找零问题也变得更加复杂。未来，可能出现更加高效、灵活的算法模型，比如量子计算找零算法，能够处理传统计算机无法解决的规模和复杂度。研究人员和工程师将不断探索新的理论和技术来应对这一挑战。

本文还有配套的精品资源，点击获取

简介：在Java编程中，找零钱问题是一个广泛应用的算法问题。本文将深入探讨这一问题，并提供动态规划与贪心算法两种解决方案，以及在Java中的代码实现。找零问题要求我们用最少数量的硬币组合凑出目标金额。我们通过创建数组来追踪凑出每个金额所需的最少硬币数，并采用贪心策略来选取面值最大的硬币。在实际应用中，此问题常见于电商退款处理、游戏货币兑换等场景。掌握解决此问题的算法对于Java开发者至关重要。

本文还有配套的精品资源，点击获取