中国象棋AI算法解析与源码实现

本文还有配套的精品资源，点击获取

简介：本项目致力于通过编程实现一个能与中国玩家对弈的中国象棋AI系统。涉及核心知识点包括编程实现游戏规则、搜索算法、评估函数和Alpha-Beta剪枝技术。通过这些技术，我们可以构建一个智能的AI系统，深入理解人工智能和博弈论，并提高编程能力。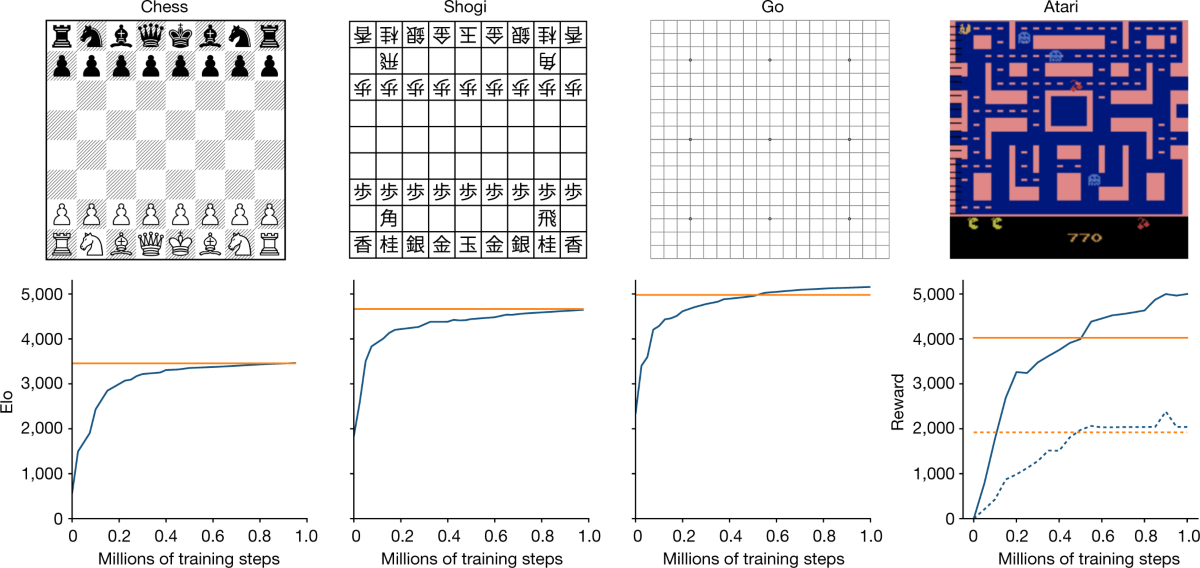

1. 中国象棋规则编程

中国象棋作为一项智力运动，其规则复杂而精细，要求编程实现时必须做到精确而高效。本章将介绍中国象棋规则的编程实现，帮助读者构建出一个稳定、可扩展的基础框架，为后续章节中棋子移动、状态表示、搜索算法、评估函数和AI技术的开发提供支撑。

1.1 中国象棋规则概述

中国象棋是一种两人对弈的策略游戏，拥有特定的棋盘布局、棋子种类和移动规则。每方共有16个棋子，包括1个帅（将）、2个士（仕）、2个象（相）、2个马、2个车、2个炮和5个兵（卒）。每种棋子都拥有独特的移动方式，例如车走直线、马走日字等。此外，还有一系列特殊规则，如“将军”和“将死”，这些都必须在编程实现时精确地表达出来。

1.2 规则的编程实现方法

编程实现中国象棋规则，首先需要定义棋盘和棋子的数据结构。通常使用二维数组表示棋盘，每个棋子用结构体或类表示，包含其位置、类型等信息。接着，将所有规则转化为一系列函数，如 movePiece 来移动棋子， checkForCheck 来判断将军状态等。对于特殊规则，如“将军”和“将死”，可以利用状态表示中的特定标识位来处理。

class ChessPiece {
public:
    int x, y; // 棋子的位置坐标
    int type; // 棋子的类型
    bool isRed; // 棋子的颜色标识，红方或黑方

    // 棋子移动函数，根据棋子类型和规则实现具体移动逻辑
    void move(int newX, int newY, ChessBoard& board);
};

// 棋盘类
class ChessBoard {
public:
    ChessPiece board[10][9]; // 中国象棋的棋盘大小为10行9列

    // 执行移动并更新棋盘状态的函数
    bool performMove(int startX, int startY, int endX, int endY);
};

通过上述方法，我们可以将中国象棋的规则逻辑转变为程序能够理解和操作的形式，为后续章节中更高级的算法和策略实现打下坚实的基础。

2. 棋子移动规则和状态表示

棋类游戏的编程实现首先需要解决的问题就是如何表示游戏的棋盘、棋子以及它们的状态，并能够正确地根据规则实现棋子的移动。这不仅是游戏逻辑的核心，也是实现智能算法的基础。

2.1 棋子移动规则的逻辑实现

2.1.1 棋子的基本移动模式

每种棋子在中国象棋中有其特定的移动规则。例如，车可以沿直线前进或横向移动直到遇到其他棋子；马走“日”字，也就是先直线移动一格，再横向移动一格；象（相）和士（仕）的移动则分别被限制在田字格和斜线方向上。这些规则需要通过编程逻辑来精确实现。

# 示例：车的移动规则实现
def move_rook(position, direction, board):
    x, y = position
    moves = []
    if direction == 'horizontal':
        for i in range(0, 9):
            if i != x:
                moves.append((i, y))
    elif direction == 'vertical':
        for j in range(0, 10):
            if j != y:
                moves.append((x, j))
    # 移动时需要检查路径上是否有其他棋子阻挡
    return [m for m in moves if not board.is_piece_at(m)]

# 假设board是一个棋盘对象，具有is_piece_at方法用于检测位置上是否有棋子

在这个例子中， move_rook 函数负责生成车移动的合法位置列表。它首先确定车的移动方向，然后遍历棋盘上的每个位置，如果位置不在当前位置的同行或同列，则将其添加到可能的移动列表中。最后，它返回一个没有其他棋子阻挡的合法移动列表。

2.1.2 特殊规则如“将军”、“将死”的判定

除了基础移动规则，中国象棋还有“将军”和“将死”这样的特殊规则。实现这些规则需要对棋盘状态进行更复杂的检查，确保符合规则的逻辑。

# 示例：检查将军状态
def is_check(state):
    # 这里的state是一个包含棋盘状态的对象
    for piece in state.pieces:
        if piece.color != state.current_player:
            continue
        for move in piece.get_possible_moves(state.board):
            if state.is_king_in_check(move):
                return True
    return False

这段代码代表了判断当前玩家是否被将军的逻辑。函数 is_check 遍历当前玩家的所有棋子，对于每一种棋子，它检查所有合法的移动。如果在某个移动之后，对方的将（帅）处于被攻击状态（使用 state.is_king_in_check(move) 来检查），则当前玩家处于被将军状态。

2.2 状态表示与数据结构设计

为了使程序能够正确处理棋盘上的移动和状态变化，需要合理设计存储和表示棋盘状态的数据结构。

2.2.1 棋盘的数据存储方式

棋盘的存储可以通过多维数组来表示，其中索引对应棋盘上的位置，数组中的元素代表棋子。

# 示例：棋盘的数组表示
class ChessBoard:
    def __init__(self):
        self.board = [[None for _ in range(9)] for _ in range(10)]

    def place_piece(self, piece, position):
        self.board[position.x][position.y] = piece

    def remove_piece(self, position):
        self.board[position.x][position.y] = None

这里定义了一个 ChessBoard 类，它使用一个10x9的二维数组来表示棋盘。 place_piece 方法用于放置棋子，而 remove_piece 用于移除棋子。通过这样的数据结构，可以很方便地操作棋盘。

2.2.2 棋局状态的编码方法

棋局的状态需要编码以便于计算机处理和存储。例如，可以使用特定的字符串或数字来唯一标识每种棋子和空格，从而实现编码。

# 示例：棋子和空格的编码表示
PIECE Encoding = {
    'None': 0,
    'King': 1,
    'Advisor': 2,
    'Elephant': 3,
    'Horse': 4,
    'Chariot': 5,
    'Cannon': 6,
    'Soldier': 7
}

# 使用二维数组表示棋盘
board_array = [[PIECE_ENCODING[piece] for piece in row] for row in chess_board.board]

通过上述方式，一个棋盘就可以被编码为一个二维数组 board_array ，其中每个元素是一个数字，对应于 PIECE_ENCODING 中定义的棋子或空格。这样，整个棋盘状态就可以很容易地被计算机读取和操作了。

在接下来的章节中，我们将进一步探索如何实现搜索算法，以及如何优化这些算法以提升中国象棋AI的性能。

3. 搜索算法Minimax实现

3.1 Minimax搜索算法原理

3.1.1 算法的基本思想和递归结构

Minimax搜索算法是一种经典的决策策略，广泛应用于有零和游戏特性的回合制游戏中，如中国象棋、国际象棋、井字游戏等。其核心思想是找到最优策略，确保在最坏情况下能够达到最好的结果。Minimax算法递归地遍历游戏树，从叶子节点评估到达该节点的棋局的得分，然后在每个节点处选择能够使对手最差情况得分最小化的最佳移动。

在实现Minimax算法时，通常会有一个递归函数来处理搜索过程。这个函数需要两个参数：当前的棋局状态和当前的深度（也称为“ply”）。递归的终止条件通常是到达了树的叶子节点，即游戏的结束状态或者达到了预设的最大搜索深度。

def minimax(position, depth):
    if depth == 0 or position.is_terminal():
        return position.evaluate()
    if position.player == MAX:
        return max_value(position, depth)
    else:
        return min_value(position, depth)

def max_value(position, depth):
    v = -INFINITY
    for each in position.successors():
        v = max(v, minimax(each, depth - 1))
    return v

def min_value(position, depth):
    v = INFINITY
    for each in position.successors():
        v = min(v, minimax(each, depth - 1))
    return v

在上面的代码中， minimax 函数是主要的搜索函数，它根据当前玩家是最大值（MAX）还是最小值（MIN）玩家，调用 max_value 或 min_value 函数。 evaluate 函数用于评估叶子节点的得分，而 successors 函数用于生成给定棋局的所有可能后续状态。

3.1.2 极大极小值和博弈树构建

在构建博弈树时，Minimax算法需要考虑所有可能的移动和对应的对手反应。对于一个简单的两层树，例如当前玩家（MAX）做决策后，对手（MIN）再做一次决策，算法将评估所有可能的最终局面，并选择得分最高的一条路径。

为了构建这样的树，需要创建一个递归结构，其中每个节点代表一个游戏状态，而分支代表从一个状态可能到达的其他状态。算法从根节点开始，递归地对树进行评估。在树的叶子节点，得分是根据评价函数进行评估的，通常是根据棋子位置、棋局的控制程度等信息计算得出。在非叶子节点，MAX玩家选择最大得分，而MIN玩家选择最小得分。

为了更高效地评估树，通常会采用剪枝技术。通过剪枝，可以在不影响最终决策结果的情况下减少评估的节点数量。例如，Alpha-Beta剪枝技术可以在不影响最终决策结果的情况下，显著减少搜索树的大小，从而减少计算量。

3.2 搜索算法的优化策略

3.2.1 反作弊剪枝技术

在搜索算法中实施反作弊剪枝技术，主要是为了防止算法在不同棋局状态下重复相同的错误。这通常是因为算法在评估分支时未能考虑全局最优策略，导致对某些局面判断失误。通过反作弊剪枝，可以在搜索过程中对已知的或潜在的“作弊”行为进行剪枝，避免算法陷入局部最优。

实现反作弊剪枝的一种方法是设置一些启发式规则，当算法遇到某些特定的局面时，立即跳过评估当前节点，认为其不具备进一步探索的价值。比如，在国际象棋中，如果一个马在开局阶段就陷入被对方两个兵夹击的位置，算法会认为这种局面非常不利，从而剪枝。

def heuristic_pruning(position):
    # 示例启发式规则：如果马的位置非常不利，则剪枝
    knight = position.get_knight()
    if knight.is_pinned() or knight.is_trapped():
        return True
    return False

在上述代码中， heuristic_pruning 函数使用启发式规则来判断当前局面是否应该被剪枝。如果马的位置被判定为非常不利，该函数返回True，表明当前节点应该被剪枝。

3.2.2 迭代深化搜索与裁剪

迭代深化是一种优化搜索算法的策略，它逐步增加搜索深度直到达到预设的最深节点或者计算资源耗尽。这种策略允许算法首先评估更少的节点，然后逐步增加深度，每一层都利用之前层的评估结果。通过迭代深化搜索，可以在有限的时间内获得更深层次的搜索效果。

迭代深化与裁剪的结合使用，能够在保证算法性能的同时提高决策的质量。裁剪技术可以减少不必要的节点评估，特别是在迭代深化的每一层中，通过判断当前节点是否有可能在更深层次中被剪枝来决定是否继续搜索。

def iterative_deepening(position, max_depth):
    best_score = -INFINITY
    for depth in range(1, max_depth + 1):
        score = minimax(position, depth, -INFINITY, INFINITY)
        if score > best_score:
            best_score = score
        # 如果当前得分已经不可能被超过，则停止搜索
        if best_score >= INFINITY - depth:
            break
    return best_score

在上述代码中， iterative_deepening 函数在预设的最大深度范围内逐步增加深度进行搜索。它会记录在每一层深度中找到的最佳得分，并在得分不再增加或已不可能被超过时停止搜索。

4. Alpha-Beta剪枝技术应用

4.1 Alpha-Beta剪枝原理与实现

4.1.1 Alpha-Beta剪枝的理论基础

Alpha-Beta剪枝是计算机博弈论中一种重要的优化技术，尤其在实现棋类游戏AI时被广泛应用。Alpha-Beta剪枝技术的核心思想是减少搜索树节点的数量，通过剪掉那些对最终结果无影响的分支来提高搜索效率。它利用了极小化极大和极大化极小的策略来提前终止那些不可能带来更优解的分支。

在没有剪枝技术的情况下，我们需要遍历搜索树中的每一个节点来寻找最优解，这在计算上是不可行的，尤其是在复杂游戏中。Alpha-Beta剪枝通过维护两个值，Alpha和Beta，来记录当前已经搜索到的最优值。Alpha代表最优解对于极小化玩家来说的最大可能值，而Beta代表最优解对于极大化玩家来说的最小可能值。当搜索过程中的任何部分发现当前的最优值已经无法影响最终的胜局时，搜索将提前终止该分支。

4.1.2 剪枝技术在搜索过程中的应用

在实际的应用中，Alpha-Beta剪枝技术是在Minimax算法的框架下实现的。在Minimax搜索算法中，算法会递归地在树状结构中搜索所有可能的移动和对应的响应，以期望找到最佳的移动。每一层代表了游戏的一个状态，其中一方选择一个移动，下一层代表对方的可能响应。

当算法向下搜索时，它会持续更新Alpha和Beta值。一旦发现任何节点的值已经小于Alpha或大于Beta，意味着该节点的移动不可能成为最终的最优解，因此可以停止对这些节点的进一步探索。这样，只有那些可能改善当前最优解的移动会被考虑，大大减少了搜索树的大小。

在实现Alpha-Beta剪枝时，我们通常采用一种称为“NegaScout”的技术，也称为“PVS”（Principal Variation Search）。NegaScout技术允许更快地剪枝，因为搜索的顺序得到优化，并且在很多情况下，它比标准的Alpha-Beta实现更高效。

接下来，我们通过代码块来展示如何实现Alpha-Beta剪枝算法的基础逻辑。

# 伪代码展示 Alpha-Beta 剪枝的实现

def alpha_beta(node, depth, alpha, beta, maximizing_player):
    if depth == 0 or node.is_terminal():
        return node.evaluate()
    if maximizing_player:
        value = -float('inf')
        for child in node.get_children():
            value = max(value, alpha_beta(child, depth - 1, alpha, beta, False))
            alpha = max(alpha, value)
            if alpha >= beta:
                break # Beta剪枝
        return value
    else:
        value = float('inf')
        for child in node.get_children():
            value = min(value, alpha_beta(child, depth - 1, alpha, beta, True))
            beta = min(beta, value)
            if beta <= alpha:
                break # Alpha剪枝
        return value

在这个代码块中，我们首先定义了一个递归函数 alpha_beta ，它接受当前节点 node ，剩余搜索深度 depth ，当前已知的最佳值 alpha 和 beta ，以及一个标志 maximizing_player 来指示当前是最大化玩家还是最小化玩家的回合。函数会根据当前的 maximizing_player 标志，递归地探索所有可能的移动，并更新 alpha 和 beta 值。如果 alpha 大于或等于 beta ，则发生剪枝。

4.2 高效的剪枝算法优化

4.2.1 剪枝启发式方法

为了进一步提高Alpha-Beta剪枝算法的效率，我们可以应用启发式方法。启发式方法基于领域知识来引导搜索过程，以便更快地找到最优解。在Alpha-Beta剪枝中，启发式方法可以用来确定哪些节点更有可能是好的移动，并优先探索这些节点。

启发式方法的一个例子是使用历史启发式，其中算法会记录每个移动在之前游戏中的成功率。成功的移动会有更高的优先级，因此在搜索过程中会首先被考虑。此外，还有递归剪枝启发式方法，例如“killer heuristic”，其中任何导致beta剪枝的移动都被认为是强有力的，并被记录在特定的列表中。下次递归搜索时，这些“杀手”移动会被优先考虑。

4.2.2 剪枝优化的效果评估

为了评估剪枝算法的优化效果，我们需要观察搜索树的节点被访问的次数以及搜索所需的时间。一种常用的评估方法是观察被剪枝的节点百分比。如果一个算法的剪枝率很高，这通常意味着它非常高效，因为它能更快地排除非最优的移动。

此外，我们可以比较在不同深度下搜索时的节点访问量。深度增加时，搜索树的节点数呈指数增长，但有效的剪枝技术能够减缓这一增长趋势。通过对比优化前后的节点访问量，我们可以判断剪枝优化的效果。

我们还可以通过实际对弈中AI的表现来评估剪枝优化的效果。通过记录AI在实际对弈中的胜率、均分和其他相关统计信息，我们可以分析剪枝优化对于提高AI整体表现的贡献。

最后，对于一个剪枝算法来说，它还应该能够在保持算法效率的同时，提供稳定的胜率。因此，在评估剪枝技术时，还需要考虑它在不同游戏中的鲁棒性。

在进一步优化剪枝算法时，还可以考虑并行计算和机器学习技术。并行计算可以同时在多个节点上运行搜索，而机器学习，尤其是强化学习，可以用于训练神经网络来帮助评估棋局的优劣。这些都是未来可能的剪枝算法优化方向。

5. 评估函数设计

5.1 评估函数的作用和构建原则

5.1.1 评估函数在AI决策中的重要性

评估函数在棋类游戏AI中扮演着至关重要的角色。它负责对棋局的当前状态进行评分，以此来指导AI进行下一步的决策。简而言之，评估函数就像是AI的“大脑”，它决定了AI如何对棋盘上的局势进行评估和判断。评估分数的高低直接影响AI选择走子的策略。

5.1.2 设计评估函数的方法论

评估函数的设计并不是一件简单的事情，它需要综合考量棋子的价值、棋局的控制、棋型的优劣、威胁与反威胁、以及未来可能的发展方向等因素。一个良好的评估函数应该能够准确反映出当前局面的优劣，并且在搜索算法的指导下，帮助AI选择出最佳的走法。

5.2 评估函数的具体实现与调优

5.2.1 各类棋子的权重设置

在评估函数中，为不同的棋子设置合理的权重是非常关键的。通常来说，将（帅）的价值是最高的，其次是士（仕）、象（相）、马、车、炮、兵（卒）。权重的具体数值需要通过实验和大量对局来调优，以保证评估函数能够尽可能地接近人类专家的评分标准。

以下是一个简单的示例，展示了如何为不同的棋子设置权重：

# 棋子权重设置示例
piece_values = {
    '将': 9.0,  # 将的权重最高
    '士': 3.0,  # 其次是士
    '象': 3.0,  # 象的权重与士相同
    '马': 2.5,
    '车': 3.5,
    '炮': 2.0,
    '兵': 1.0,
}

5.2.2 基于局面的动态调整方法

评估函数需要能够根据棋局的具体情况动态调整评分。例如，在中盘时，炮的价值可能会因其位置和牵制能力而增加；而在残局时，车的价值会因能够直接影响战斗结果而提高。此外，评估函数还应该考虑棋局中是否存在“将军”、“将死”的情况，或者有无潜在的攻击手段。这些因素都需要通过特定的算法逻辑来实现动态调整。

def dynamic_adjustment(board):
    # 一个动态调整评分的算法示例
    score = 0
    for piece in board.get_all_pieces():
        piece_value = piece_values[piece.type]
        position_score = position_matrix[piece.position]  # 一个根据位置调整得分的矩阵
        if piece.is_under_attack():
            score -= piece_value  # 如果棋子受到威胁，扣分
        else:
            score += piece_value + position_score  # 否则加分
    # 添加其它动态调整的逻辑...
    return score

以上内容仅为评估函数设计中的简单说明和代码片段示例。在实际应用中，评估函数的设计通常更加复杂和深入，需要进行大量的测试和调优，以确保其能够准确评估棋局局势，指导AI作出正确的决策。

本文还有配套的精品资源，点击获取

简介：本项目致力于通过编程实现一个能与中国玩家对弈的中国象棋AI系统。涉及核心知识点包括编程实现游戏规则、搜索算法、评估函数和Alpha-Beta剪枝技术。通过这些技术，我们可以构建一个智能的AI系统，深入理解人工智能和博弈论，并提高编程能力。

本文还有配套的精品资源，点击获取