训练/测试集, 偏差/方差(欠拟合/过拟合), 正则化/权重衰减

1. 训练集 / 验证集 / 测试集

• 数据划分比例:
  • 小数据量(10-10000)：60/20/20
  • 大数据量(1000000) : 98/1/1
  • 超大数据量: 99.5/0.25/0.25
• 在不需要无偏评估的时候可以不需要测试集, 只有训练集和验证集. 如果需要验证集来微调参数, 就需要再划分出测试集来做无偏评估.

2. 偏差 / 方差

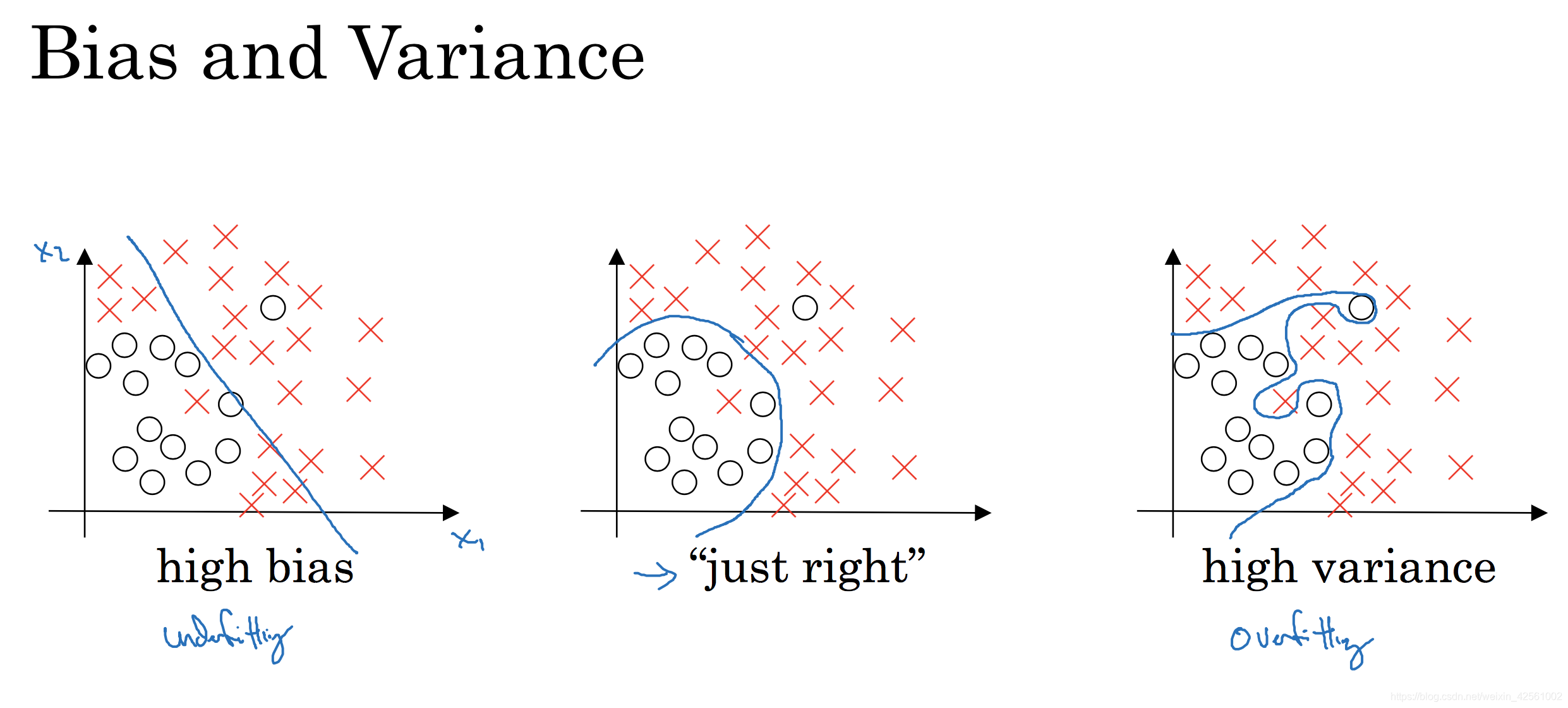
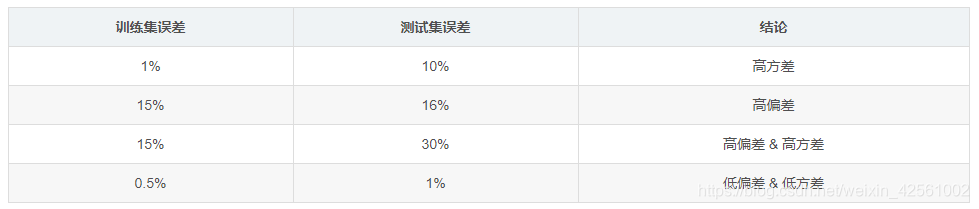
1. 高偏差：欠拟合
   解决方法:
   • 使用更大的网络或者更复杂的模型
   • 训练更长的时间（不一定好使）
   • 使用更好的优化算法
2. 高方差：过拟合
   解决方法:
   • 获取更多的数据
     • 收集更多源数据
     • 数据扩增
   • 使用更合适的模型
     • 简化模型结构
     • early stopping
     • 添加正则项(正则化)
   • 集合多种模型
     • bagging
     • dropout
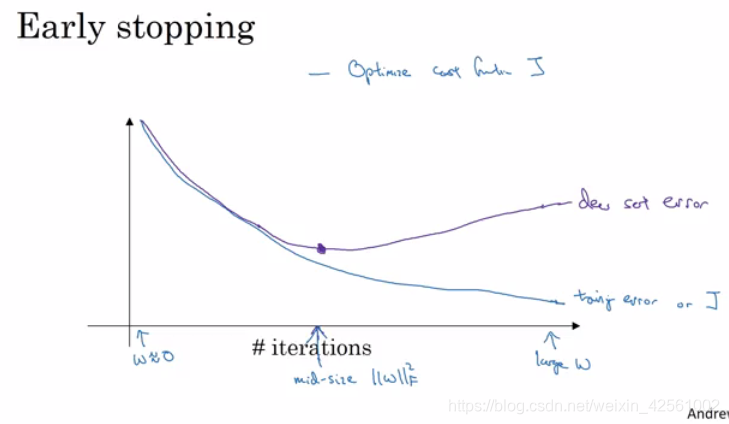
3. 如何做early stopping?
   答: 在每一个epoch/iteration/多个iteration结束之后计算一下validation set cost, 当validation set cost不再降低或者开始升高的时候, 就可以提前停止了, 否则开始过拟合
   
4. PCA可以用来防止过拟合吗?
   答: 可能有用, 可能没用, 不推荐. 因为pca是无监督的, 它是按照方差大小而不是分类信息来进行特征选择, 因此方差小的那些特征上可能存在着大量分类信息却被丢掉了. 如果是别的有监督降维的方法, 对防止过拟合就有很好的效果.

3. 正则化

1. L2正则: $$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}||w|{|}_2^2$$
   $$\frac{\lambda }{2m}||w|{|}_2^2=\frac{\lambda }{2m}\sum _{j=1}^{n_x}{w}_j^2=\frac{\lambda }{2m}{w}^{T}w$$

2. L1正则:
   $$J(w,b)=\frac{1}{m}\sum _{i=1}mL({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{m}||w|{|}_1$$
   $$\frac{\lambda }{m}||w|{|}_1=\frac{\lambda }{m}\sum _{j=1}^{n_x}|w_j|$$

3. 权重衰减:
   加入L2正则项后, 梯度变为: $$d{W}^{[l]}=(from\_backprop)+\frac{\lambda }{m}{W}^{[l]}$$
   代入梯度更新公式后变为:
   $$\begin{array}{rl}{W}^{[l]}:& =W^{[l]}-\alpha \cdot [(from\_backprop)+\frac{\lambda }{m}{W}^{[l]}]\\ & =W^{[l]}-\alpha \frac{\lambda }{m}{W}^{[l]}-\alpha (from\_backprop)\\ & =(1-\frac{\alpha \lambda }{m})W^{[l]}-\alpha (from\_backprop)\end{array}$$
   可以看到参数W相当于获得了一个小于1的系数, 因此每次更新都会衰减. 所以L2范数正则化也被称为"权重衰减"

4. 正则化怎么防止过拟合?
   答: 添加正则项相当于对模型添加了先验, 先验会惩罚复杂的模型参数, 使得越复杂的模型loss越大.
   
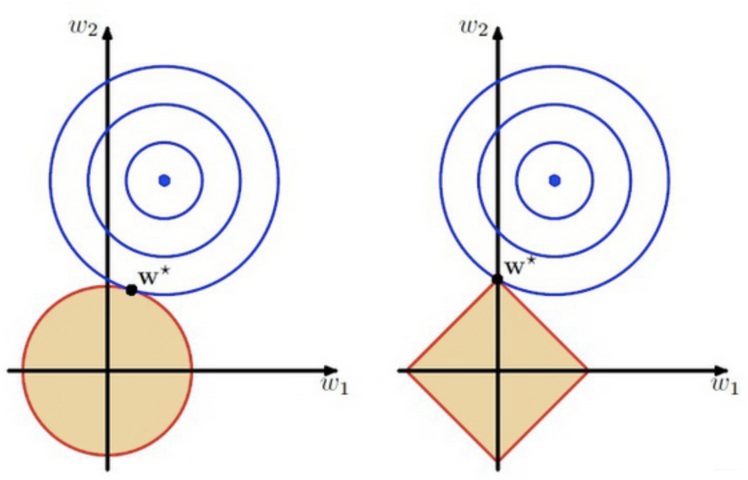
   如图, 可以认为参数W在蓝色圆心$w_o$处时模型可以100%拟合训练数据, 不加正则项的loss是$w^{\ast }$与$w_o$的距离, 正则项是$w^{\ast }$与原点的距离. 所以加上正则项后, 实际上是控制$w^{\ast }$不能太远离原点, 即模型不能太复杂.

5. L1正则和L2正则有什么区别?
   答: 两者都可以用来防止过拟合, L1为拉普拉斯先验, L2为高斯先验. L1可以产生稀疏解, 即让一部分特征的系数缩小到0, 从而间接实现特征选择, L1适用于特征之间有关联的情况. L2让所有特征的系数同时缩小, 但不会减到0, 它会使优化求解稳定快速, L2适用于特征之间没有关联的情况.

6. L1为什么相比L2更容易获得稀疏解?
   答: 看上图, 左边为L2正则, 右边为L1正则. L2中到原点的距离相等的点在圆上, L1中到原点距离相等的点在正方形上, 因此L1中最优解会落在坐标轴上, 而L2中不会.