python 蒙特卡洛模拟股价_12 Python总结之蒙特卡洛模拟

蒙特卡洛模拟

蒙特卡洛模拟是金融学和数值科学中最重要的算法之一。它之所以重要，是因为在期权定价或者风险管理问题上有很强的能力。和其它数值方法相比，蒙特卡洛方法很容易处理高维问题，在这种问题上复杂度和计算需求通常以线性方式增大。

蒙特卡洛方法的缺点是：它本身是高计算需求的，即使对于相当简单的问题也往往需要海量的计算。因此，必须高效的实现蒙特卡洛算法。

下面使用不同的方法实现蒙特卡洛算法

1.Scipy

2.纯Python

3.向量化Numpy

4.全向量化Numpy

方法一：Scipy

欧式看涨期权的定价公式Black-Scholes-Merton(1973):

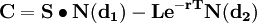
其中：

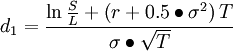
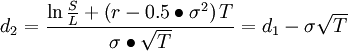
C—期权初始合理价格

L—期权交割价格

S—所交易金融资产现价

T—期权有效期

r—连续复利计无风险利率

σ2—年度化方差

N()—正态分布变量的累积概率分布函数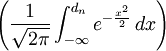

# 导用到的库

from math import log, sqrt, exp

from scipy import stats

# 期权的定价计算,根据公式１．

def bsm_call_value(S_0, K, T, r, sigma):

S_0 = float(S_0)

d_1 = (log(S_0 / K) + (r + 0.5 *sigma **2) *T)/(sigma * sqrt(T))

d_2 = (log(S_0 / K) + (r - 0.5 *sigma **2) *T)/(sigma * sqrt(T))

C_0 = (S_0 * stats.norm.cdf(d_1, 0.0, 1.0) - K * exp(-r * T) * stats.norm.cdf(d_2, 0.0, 1.0))

return C_0

# 计算的一些初始值

S_0 = 100.0 # 股票或指数初始的价格;

K = 105 # 行权价格

T = 1.0 # 期权的到期年限(距离到期日时间间隔)

r = 0.05 # 无风险利率

sigma = 0.2 # 波动率(收益标准差)

# 到期期权价值