计算机组成M代表,计算机组成原理 --- 数据信息的表示

计算机内部流动的信息可以分为两大类：一类是数据信息，另一类为控制信息。

数据信息是计算机加工处理的对象，而控制信息则控制数据信息的加工处理。

2.1 数据表示应考虑的因素

2.2 数值数据的表示

2.3 非数值数据的表示

2.4 数据信息的校验

2.1 数据表示应考虑的因素

1.数据类型 从大体上分类：数值数据和非数值数据。

2.数据表示范围和精确度 计算机所能表示的数的范围和精确度与所采用的数据类型和字长有关。

3.存储和处理的代价 设计出的数据格式要便于存储和处理。

4.软件的可移植性 设计数据格式时，要充分考虑软件的可移植性。

2.2 数值数据的表示

2.2.1 数的机器码表示

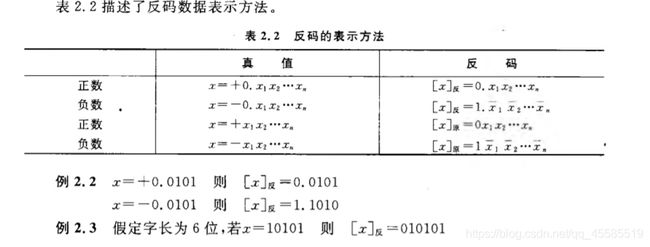
原码表示

1) 0的表示有+0根-0，两种原码表示0.000…0跟1.000…0 ;

原码表示的优点是直观，真值与原码转化简单。但是运算复杂，不利于运算器设计的简化。

反码表示

补码表示

引入补码数据表示的目的就是希望能方便带符号数的加减运算。

二进制补码的求法

1) 根据补码的定义求补码。

[x]补码 = 模 + x(mod模) ，x可正可负，利用这种方法需要事先求出 模的值。

2) 利用反码求补码

因为 [x] 补码 = [x]反 + 2^-n (n b表示小数点后的位数)

说明求一个负数的补码 ，可以在其反码的基础上通过最低位加一的方式得到。

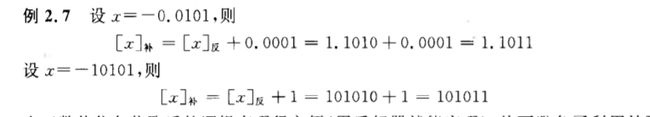
3) 利用扫描方法求补码

扫描方法可以很方便地将一个负数从真值或原码表示直接变换成 补码，具体方法是 对数值位 按照从低位到高位的顺序扫描，尾数第一个1以及其右边的0保持不变。其余各位求反，最后再将符号位置置1。

移码表示

移码可以通过真值 x 加上一个常数得到，这个常数也成为 偏置值 ，增加常数的操作相当于 x 在数轴上向正方向平移了一段距离，这就是被称为 移码 的原因，移码也可以称为 增码 。

即[x]移 = x + 偏移值。

经观察 得知 移码数据表示 具有下列特点

1) 移码的符号位中 0 表示负数 ， 1 表示 正数。

2) 同一数值的移码 与 补码除符号位相反以外，数值位相同。

3 ) 移码中 0 的表示也唯一 ， 具体表示为 100000…0。

将 移码 作为 浮点数的阶码 具有下列优点：

1 ) 移码通过偏移的方法把 真值 映射到 正数域，这样子可以直接按照无符号数规则比较两个移码表示数据的大小，便于浮点数的比较。

2) 有利于简化 “机器零” 的判断。 当移码的各位均为 0 时，对应的 阶码值 最小。因此，尾数全为0时对应的就是 机器零。

2.2.2 数的定点表示

定点表示法 约定 机器中所有数据的 小数点 位置固定，其中，将小数点位置固定在数据的最高位之前(或符号位之后)的数据表示称为 定点小数 。而将小数点固定在最低数位之后的数据表示称为 定点整数。因为小数点位置固定，因而小数点可不必再用记好表示，也无需存储。

定点小数

设定点小数 x 的形式 为 x = x0，x1，x2，…，xn ，其中 x0是符号位 ， x1 ~ xn为数值的有效部分，也称为 尾 数 ，x1 为 最高有效位。