2019-7-5 opencv中的Harris 角点检测（Harris Corner Detection ）

• Harris 角点检测原理
• Harris 角点检测在python应用

关于Harris 角点检测，官网参见https://docs.opencv.org/3.4.1/dc/d0d/tutorial_py_features_harris.html

Harris 角点检测原理

Chris_Harris 和 Mike_Stephens 于1988年在《A Combined Corner and Edge Detector》中提出发现角点的方法，就是现在被称为Harris 角点检测方法。

该方法的数学形式为：将窗口向各个方向移动（u，v）然后计算所有差异的总和。
表达式如下

窗口函数w(x,y)可以是正常的矩形窗口，也可以是对每一个像素给予不同权重的高斯窗口。
实现角点检测需要使E(u,v)最大化，也就是说必须使方程右侧的第二项的取值最大。
对上面的等式进行泰勒级数（Taylor Expansion）展开，然后再通过几步数学换算，可以得到下面的等式：

其中：

这里的 I_x 和 I_y是图像在 x 和 y 方向的导数。（使用函数 cv2.Sobel()可以很容易获得）。
然后就是关键部分了。获得上面等式之后，可以对一个等式(见下)进行打分来判定窗口内是否包含角点。

R=det(M)−k(trace(M))²

其中

• det(M) = λ₁λ₂ 。注：det表示矩阵M的行列式
• trace(M) = λ₁+λ₂ 。注：trace，或者tr，表示矩阵M的迹。
• λ₁和λ₂是M的特征值

关于矩阵的概念det和trace，参见https://baike.baidu.com/item/TR/3776614?fr=aladdin。

根据这些特征值，我们就可以根据以下条件判断一个区域是否是角点，边界或者是平面。

• 当|R| 很小（此时λ₁ 和 λ₂ 都小），这个区域就是一个平面。此时E在所有方向接近于常数。
• 当R < 0（此时λ1远大于λ2，或者λ2远大于λ1），这个区域是边缘。 此时E在某一方向上很大。
• 当R很大（此时λ₁ 和 λ₂ 都很大，λ₁ 近似 λ₂ ），这个区域就是角点。此时E在所有方向上都很大。

以上的判定结论图示如下

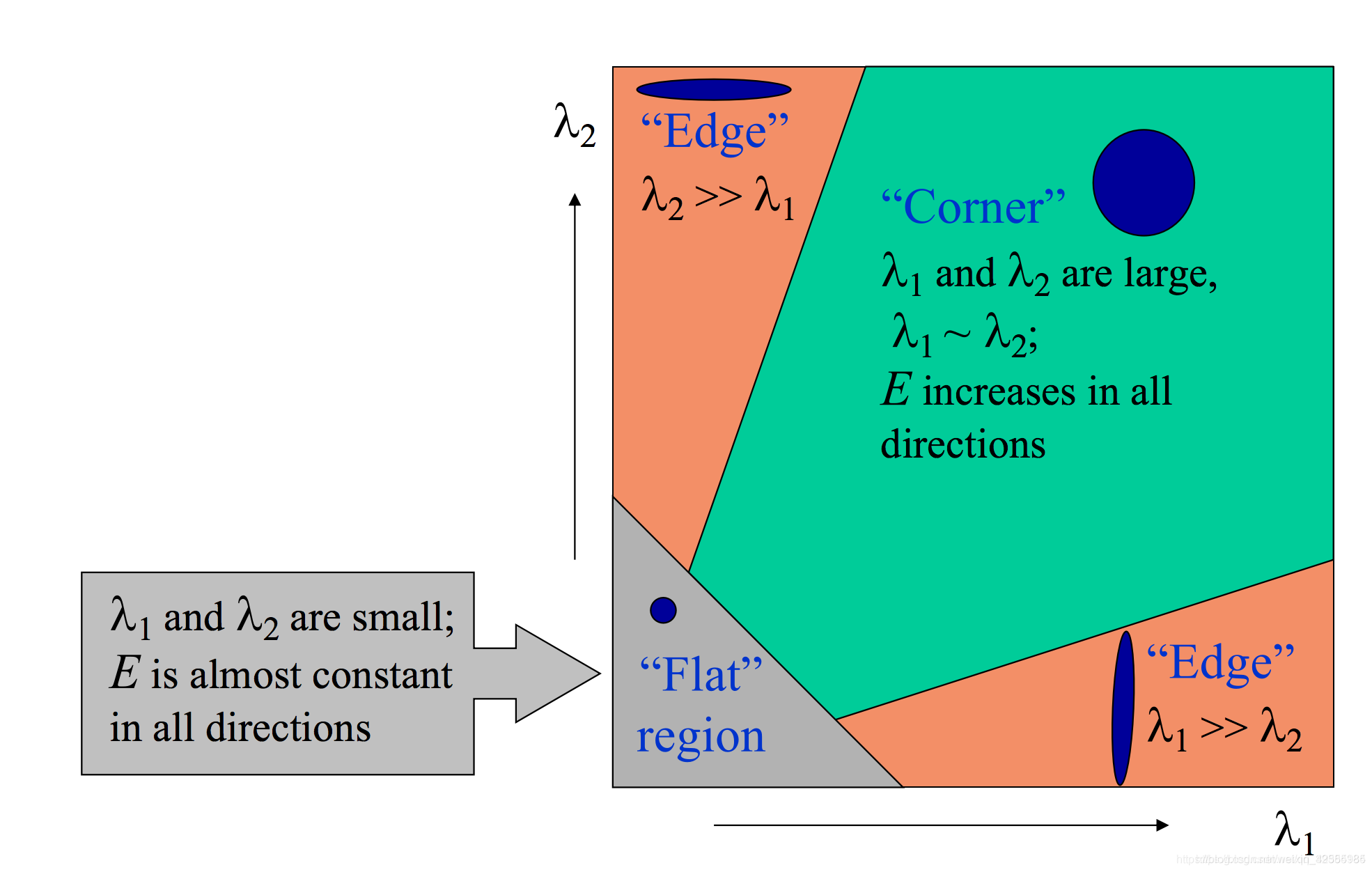
Harris 角点检测结果就是由这些评分组成的灰度图像。
选取合适的阈值-对图像二值化处理-就可以检测到图像的角点。

Harris 角点检测在python应用

opencv中Harris 角点检测函数是cornerHarris()

	dst	=	cv.cornerHarris(	src, blockSize, ksize, k[, dst[, borderType]]	)

• src ：float32 的灰度图像
• blockSize ： 角点检测中要考虑的领域大小，即：窗口函数W(x, y)大小。
• ksize ： Sobel 求导中使用的核的大小，可取1，3，5。。。（用sobel函数来得到I_x 和 I_y）
• k ： Harris 角点检测方程中的常数。默认在0.04至0.06之间。增大该值，将减小角点响应值，降低角点检测的灵敏性，减少被检测角点的数量；减小该值，将增大角点响应值，增加角点检测的灵敏性，增加被检测角点的数量。

该函数表示，对于每个像素(x，y)，计算 blockSize×blockSize 邻域上的2×2梯度协方差矩阵M^（x，y）。通过该矩阵，可以根据以下计算获得特征值

dst(x,y)=detM^(x,y)−k⋅(trM^(x,y))²

还记得上面提到的评分等式吗？R=det(M)−k(trace(M))²，是的，就是它了。
所以，当dst(x,y)局部极大时候，也就是角点位置了。

代码应用如下（参考官网）

import numpy as np
import cv2 as cv

filename = '1.jpg'
img = cv.imread(filename)
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY) #转化灰度图

gray = np.float32(gray)
dst = cv.cornerHarris(gray,2,3,0.04)

#result is dilated for marking the corners, not important
dst = cv.dilate(dst,None) #形态学运算，膨胀

# Threshold for an optimal value, it may vary depending on the image.
img[dst>0.01*dst.max()]=[0,0,255]
cv.imshow('dst',img)
if cv.waitKey(0) & 0xff == 27:
    cv.destroyAllWindows()

原图如下

运行后

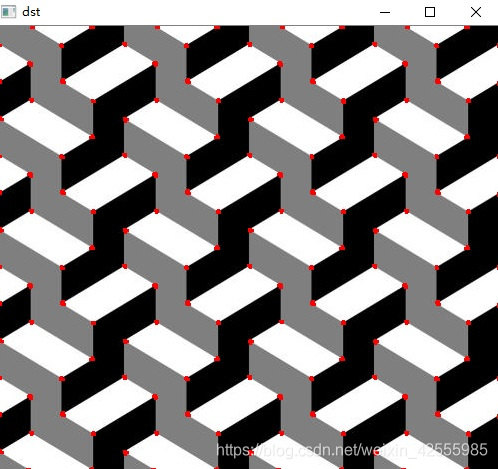
红色标注就是角点。