2020-12-13 吴恩达-C4 卷积神经网络-w4 人脸识别和神经风格转换(课后编程1-Face Recognition for the Happy House人脸识别)

使用本地的Face Recognition for the Happy House - v3.ipynb文件。

先在cmd中运行

jupyter notebook

然后打开Face Recognition for the Happy House - v3.ipynb就可以了。

欢迎来到第四周的第一个编程作业。你将构筑一个人脸识别系统。这里的许多想法来自FaceNet。在课堂中，吴恩达也讨论了 DeepFace。

人脸识别问题通常被分为两大类：

• 人脸验证：“这是不是本人呢？”，比如说，在一些机场，你可以让一个系统扫描你的护照，然后验证你（携带护照的人）是本人。又或者手机解锁能够通过人脸验证实现。这些都是1：1匹配问题。
• 人脸识别：“这个人是谁？”，比如说，在课程中的百度员工进入办公室时的脸部识别视频的介绍，无需使用另外的ID卡。这个是1：K的匹配问题。

FaceNet学习一个神经网络，它将人脸图像编码成128个数字的向量。通过比较两个这样的向量，你就可以确定两张图像是否是同一个人的。

在本练习中，你将

• 实现三元组损失函数。
• 使用预训练好的模型将人脸图像映射为128维编码
• 使用这些编码执行人脸验证和人脸识别

在这个练习中，我们将使用一个预先训练过的模型，它使用的是“通道优先”约定代表卷积网络的激活，而不是在课程和之前的编程作业中使用的“通道最后”约定。换句话说，数据的维度是(m,$n_C$ ,$n_H$ ,$n_W$ ) 而不是(m ,$n_H$ ,$n_W$ ,$n_C$) 。这两种约定在开源实现中都有相当大的吸引力；在深度学习社区中还没有一个统一的标准。

先让我们导入库。

from keras.models import Sequential
from keras.layers import Conv2D, ZeroPadding2D, Activation, Input, concatenate
from keras.models import Model
from keras.layers.normalization import BatchNormalization
from keras.layers.pooling import MaxPooling2D, AveragePooling2D
from keras.layers.merge import Concatenate
from keras.layers.core import Lambda, Flatten, Dense
from keras.initializers import glorot_uniform
from keras.engine.topology import Layer
from keras import backend as K
K.set_image_data_format('channels_first')
import cv2
import os
import numpy as np
from numpy import genfromtxt
import pandas as pd
import tensorflow as tf
import sys
tf.compat.v1.disable_eager_execution()

from fr_utils import *
from inception_blocks_v2 import *

#%matplotlib inline
#%load_ext autoreload
#%autoreload 2

#np.set_printoptions(threshold=np.nan) 
#出错threshold must be non-NAN, try sys.maxsize for untruncated representation

np.set_printoptions(threshold=sys.maxsize)

这里需要用到opencv，可以先安装

pip install opencv-python
Collecting opencv-python
  Downloading https://pypi.tuna.tsinghua.edu.cn/packages/b5/73/62568302eeff97fd0fb4517f94cb4693ecfc0f890c21f9def587d9229379/opencv_python-4.4.0.46-cp36-cp36m-win_amd64.whl (33.5MB)
    100% |████████████████████████████████| 33.5MB 30kB/s
Requirement already satisfied: numpy>=1.13.3 in c:\users\toddc\anaconda3\envs\tensorflow\lib\site-packages (from opencv-python)
Installing collected packages: opencv-python
Successfully installed opencv-python-4.4.0.46
You are using pip version 9.0.1, however version 20.3.1 is available.
You should consider upgrading via the 'python -m pip install --upgrade pip' command.

如果遇到报错如下

ValueError: threshold must be non-NAN, try sys.maxsize for untruncated representation

可以修改代码如下

#np.set_printoptions(threshold=np.nan) 
#出错threshold must be non-NAN, try sys.maxsize for untruncated representation

np.set_printoptions(threshold=sys.maxsize)

0-简单的人脸验证

人脸验证，你需要对于给出两张照片判断是否是同一个人。最简单的方法是逐像素比较两个图像。如果2个原始图像之间的距离小于选定的阈值，则可能是同一个人！

当然，该算法的性能非常差，因为像素值会因光线变化、人脸方位变化、甚至头部位置的微小变化等而发生显著变化。

你将看到，与使用原始图像不同，你可以学习编码$f(img)$。这种编码的元素比较可以更准确地判断两张图片是否是同一个人的。

1-把人脸编码为128维向量

1.1-使用卷积进行编码

FaceNet模型需要大量的数据和长时间的训练。因此，按照应用DL设置中的常见实践，让我们来加载其他人已经训练过的权重。在网络的架构上我们遵循Szegedy et al.等人的Inception模型。这里我们提供了Inception模型的实现方法，你可以在inception_blocks.py文件中看看如何实现。

你需要了解的关键信息包含：

• 网络使用96x96的RGB图像做为输入。具体来说，输入一个脸部图像张量tensor（或者一批m个脸部图像），维度为 $(m,n_c,n_h,n_w)=(m,3,96,96)$.
• 输出形状为 $(m,128)$的矩阵，把每个输入的脸部图像编码为128维向量。

运行下面的代码来创建一个人脸图像的模型

FRmodel = faceRecoModel(input_shape=(3, 96, 96))

print("Total Params:", FRmodel.count_params())

运行结果

Total Params: 3743280

通过使用128个神经元全连接层作为最后一层，该模型确保输出是一个大小为128的编码向量。然后使用编码比较两个人脸图像，如下所示：

如上图，通过计算两个编码和阈值之间的距离，可以确定这两幅图是否代表同一个人。

因此，如果满足下面两个条件的话，编码是一个比较好的方法：

• 同一个人的两个图像的编码非常相似。
• 两个不同人物的图像的编码非常不同。

三元组损失函数将上面的形式实现，它会试图将同一个人的两个图像（Anchor和Positive）的编码“拉近”，同时将两个不同人的图像（Anchor和Negative）进一步“分离”。

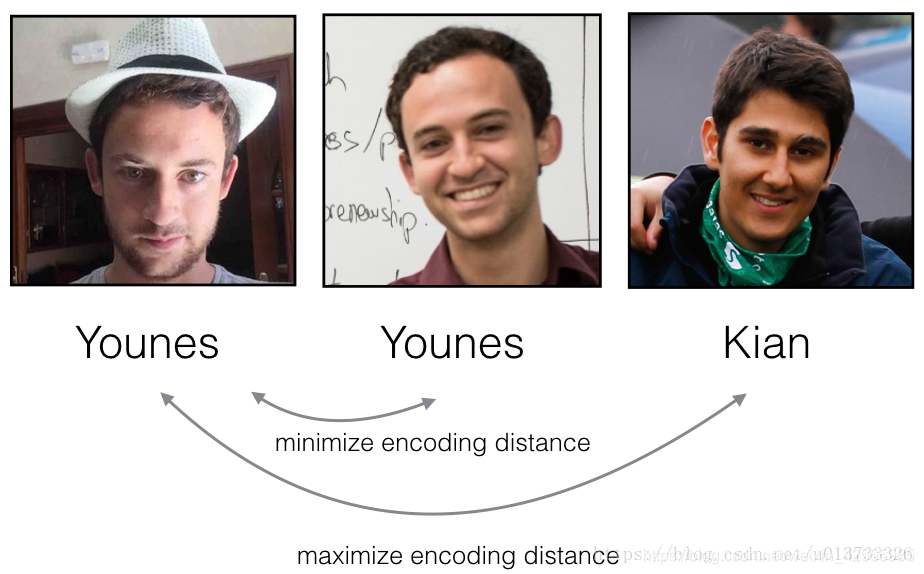
在下一部分中，我们将从左到右调用上面的图片： Anchor (A), Positive §, Negative (N)

1-3.三元损失函数

对于图像$x$，其编码表示为$f(x)$ ，其中 $f$为神经网络的计算函数。

使用三元组图像$(A，P，N)$ 进行训练：

• A： "Anchor"图像，是一个人的图像
• P： "Positive"图像，是和“Anchor”图像同一个人的另外一张图像。
• N： "Negative"图像，是和“Anchor”图像不同人的另外一张图像。

这些三元图像是我们从数据集中挑选出来的。我们使用$(A^{(i)},P^{(i)},N^{(i)}$