图论解油瓶分油问题_直流电阻网络的图论/线性代数解法

G.Strang 的 《Introduction to Linear Algebra》第 8 章第 2 节讲线性代数在图论上的应用。前一阵为了美赛，把这部分学了一下，发现正好解决了我的一个构想——编程求解直流电阻网的问题。高中物竞学这部分时，只知道用基尔霍夫方程组可以列出来一堆线性方程，然后用高斯消去法去解，但是如何让计算机去对每一条回路列方程却是有些困难的。现在学到了这个基于一点点图论的方法，便可以在给定电阻网络（以图的形式）的情况下很方便地求解了。

对于一个有 n 个节点、m 条边的有向图，各节点（Node）依次编为

,各边（Edge）编为

，可以定义其关联矩阵（Incidence Matrix）：

，其中，

.

书中给的例子：

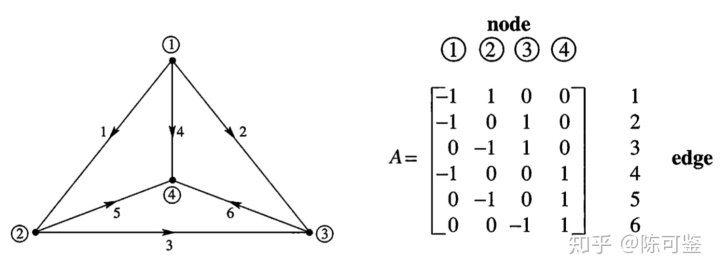
有趣的是，对矩阵 A 做行约化，得到的行最简型矩阵恰对应原图的一个生成树（因为线性相关的行对应了图中的一个 Loop）。由于最小生成树的边数为 n-1，可知矩阵 A 的秩

.

一个直流电阻网，在指定各边的正向后，可以直接看作一个连通有向图。那么电阻网的性质和关联矩阵 A 有什么关系呢？我们来看看 A 作用在某个向量 x 上的结果：

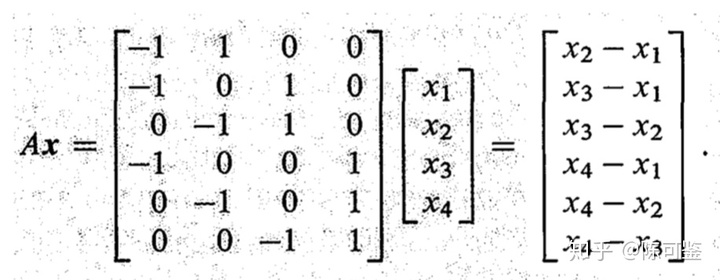
矩阵乘法要求 x 必须有 n=4 个元，那么我们很自然地认为 x 对应于 n 个节点上的值。我们发现，Ax 给出了m 条边的两端点值之差。这启发我们，如果把 n 维列向量 x 记作

，代表各节点的电势，那么

m 维列向量

就给出了各边上的电压（电势差）

。

接下来，我们看看

代表什么（书里在考察 A 的四个子空间的性质时自然地引到这个问题，我们没有太关注子空间，所以这里未必那么自然）。

类似地，矩阵乘法要求 y 必须有 m=6 个元，那么我们很自然地认为 y 对应于 m 条边上的值。观察

,不难发现这其实给出了每个节点上的「净流出」量（负数代表流入）。这启发我们，

如果把 m 维列向量 y 记作

，代表各边上的电流（正方向沿边的定向），那么

n 维列向量

就给出了流入各节点的电流

。

为了把电流和电压联系起来，我们还缺一个方程——欧姆定律。欧姆定律指出，

，R 为电阻，C 为电导。用上述向量表达，就是

,这里

是将各边电导排成的对角阵，负号表示电流沿电势下降的方向。

综合上述三式，得到：

一般情况下，我们的物理问题总是给定各个节点上的电压或注入的电流，因此，将上三式合并，得到：

这就是求解电阻网问题的核心方程了。注意到矩阵

是个 n 阶方阵，而其秩为 n-1 ，所以这个方程的解其实有一个自由度，即 A 的零空间。可以证明，A 的零空间的基底是

，所以这个自由度实际上对应了各节点的电压升高 or 降低同一数值，也即电势基准点的任意选取，这也是符合物理的。

---

后面还有关于已知量的讨论和求解的代码，过一阵再放上来吧……

头一次用知乎记笔记，若有疏漏请指正。