
Paper:https://arxiv.org/pdf/1609.02907.pdf
2017 LCLR - Semi-Supervised Classification with Graph Convolutional Networks
摘要
本文作者提出了一种可扩展的方法,用于在图结构数据上进行半监督学习,该方法基于一种直接作用于图的卷积神经网络的有效变体。通过图卷积的局部一阶近似激发卷积架构的选择。模型在图边缘数量上线性缩放,并学习对局部图结构和节点特征进行编码的隐层表示。在引文网络和知识图数据集上的大量实验中,证明了该方法在很大程度上优于相关方法。
模型
傅里叶变换
传统的傅里叶变换如下:
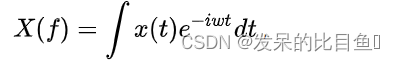
其中,x(t)x(t)x(t)是空域表示, X(f)X(f)X(f)是频域表示, e−iwte^{-iwt}e−iwt是基函数
作者发现以e−iwte^{-iwt}e−iwt为基的拉普拉斯算子是:
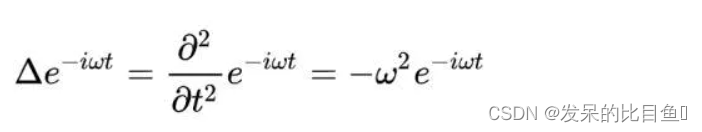
对照AV=λVAV=\lambda VAV=λV,可以发现,傅里叶变换中的基其实对照过来是矩阵的特征向量,那么将矩阵替换成图拉普拉斯矩阵,就是:LU=λULU=\lambda ULU=λU,那么这个UUU应该也可以做为图傅里叶变换的基。
于是,作者定义图拉普拉斯矩阵的特征向量可以做图傅里叶变换的基,得到:
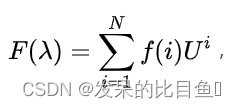
f(i)f(i)f(i)是第个iii点的信号,λ\lambdaλ是特征值。
Graph中的快速卷积
使用神经网络模型 f ( X , A ) f(X,A)f(X,A) 对所有带标签节点进行基于监督损失的训练。
XXX为输入数据
AAA为图的邻接矩阵
在图的邻接矩阵上调整 f()˙f(\dot)f()˙将允许模型从监督损失L0L_0L0中分配梯度信息,并使其能够学习所有节点(带标签或不带标签)的表示。
具有以下分层传播规则的多层图形卷积网络(GCN):
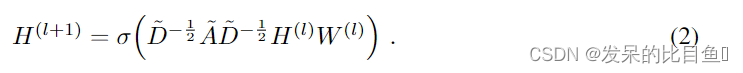 其中:
其中:
- A~=A+IN\tilde{A}=A+I_NA~=A+IN为无向图G的带自环邻接矩阵
- INI_NIN为单位矩阵
- D~ij=∑jA~ij\tilde{D}_{ij}=\sum_{j}\tilde{A}_{ij}D~ij=∑jA~ij
- WlW^{l}Wl为layer-specific可训练权重向量
- σ(.)\sigma(.)σ(.)为激活函数,例:ReLU
- Hl∈RN×DH^{l}\in R^{N \times D}Hl∈RN×D为第lthl^{th}lth 层的激活矩阵;H0=XH^{0}=XH0=X
第一种卷积

- xxx为图节点的特征向量
- gθ=diag(θ)g_θ=diag(θ)gθ=diag(θ)为卷积核,其中θθ\thetaθθθ为参数
- UUU为图的拉普拉斯矩阵LLL的特征向量矩阵
- 其中拉普拉斯矩阵L=IN−D−12AD−12=UΛUTL=I_N-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=U\Lambda U^TL=IN−D−21AD−21=UΛUT
可以看到,上面公式就是上面引用中第一代GCN所使用的卷积公式,作者在论文中也提到,这个公式的缺点在于计算太过复杂,卷积核的选取不合适,需要改进。
改进:第二种卷积
作者接下来说,有人提出一种卷积核设计方法,即gθ(Λ)g_{\theta}(\Lambda)gθ(Λ)可以使用切比雪夫多项式Tk(x)T_k(x)Tk(x)到KthK^{th}Kth的截断展开来近似。
切比雪夫多项式:
Tk(x)=2xTk−(x)−Tk−2(x)T_k(x)=2xT_{k-}(x)-T_{k-2}(x)Tk(x)=2xTk−(x)−Tk−2(x)
T0=1T_0=1T0=1
T1=xT_1=xT1=x
新的卷积核:
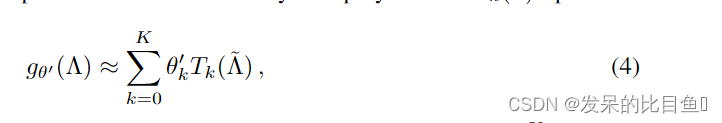
- Λ~=2Λ/λmax−IN\tilde{\Lambda}=2\Lambda/\lambda_{max}-I_NΛ~=2Λ/λmax−IN
- λmax\lambda_{max}λmax是LLL的最大特征值
- θ′∈Rk\theta ' \in R_kθ′∈Rk 是切比雪夫系数的矢量

- L~=2L/λmax−IN\tilde{L}=2L/\lambda_{max}-I_NL~=2L/λmax−IN
- 此公式为拉普拉斯算子中的KthK^{th}Kth阶多项式,即它仅取决于离中央节点最大KKK步的节点。
可以看到,公式(5)与上面引文中的第二代GCN用到的卷积公式非常相似,最终都将参数简化到了KKK个,并不再需要做特征分解,直接用拉普拉斯矩阵LLL进行变换,计算复杂性大大降低。
但本文使用了切比雪夫多项式Tk(x)T_k(x)Tk(x),这是与上面引文中提到的第二代GCN中的卷积公式的不同点。
线性模型
K=1:2个参数的模型
现在我们可以通过堆叠多个形式为公式(5)的卷积层来建立一个GCN模型。
首先,我们将分层卷积操作限制为K=1K = 1K=1 ,即关于LLL是线性的,因此在拉普拉斯谱上有线性函数。
在GCN的这个线性公式中,我们进一步近似λmax≈2\lambda_{max}\approx 2λmax≈2们可以预测到GCN的参数能够在训练中适应这一变化,此时公式(5)将简化为下式:
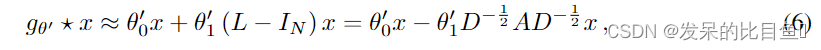
- 此公式具有两个自由参数:θ0′\theta_0 'θ0′和θ1′\theta_1 'θ1′,滤波器参数将被整个图共享
- 连续应用这种形式的滤波器,可以有效的卷积节点的kthk^{th}kth阶邻域,其中kkk是模型中连续滤波操作或卷积层的数目。
简化:1个参数的模型
令θ=θ0′=−θ1′\theta=\theta_0'=-\theta_1'θ=θ0′=−θ1′,将两个参数化为单参数θ\thetaθ,得到卷积公式如下:
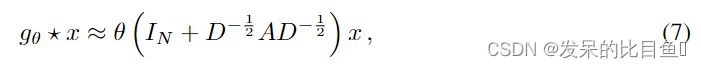
注意IN+D−12AD−12I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}}IN+D−21AD−21拥有范围为[0,2][ 0 , 2 ][0,2]的特征值,这将会导致数值不稳定性和梯度爆炸/消失。因此我们介绍下面的归一化技巧:
IN+D−12AD−12→D~AD~−12I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\rightarrow\tilde{D}A\tilde{D}^{-\frac{1}{2}}IN+D−21AD−21→D~AD~−21
- A~=A+IN\tilde{A}=A+I_NA~=A+IN
- D~ij=∑jAij~\tilde{D}_{ij}=\sum_{j}\tilde{A_{ij}}D~ij=∑jAij~
推广:特征映射公式
将该定义推广到具有CCC个输入通道(即每个节点的CCC维特征向量)的信号X∈RN×CX \in R^{N \times C}X∈RN×C, 和FFF个滤波器,则特征映射(feature maps)如下:
Z=D~−12A~D~−12Z=\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}Z=D~−21A~D~−21
- Θ∈RC×F\Theta \in R^{C \times F}Θ∈RC×F 是滤波器参数矩阵
- Z∈RN×FZ \in R^{N \times F}Z∈RN×F是卷积后的信号矩阵
半监督节点分类
一个整体的多层半监督GCN模型如下图所示:
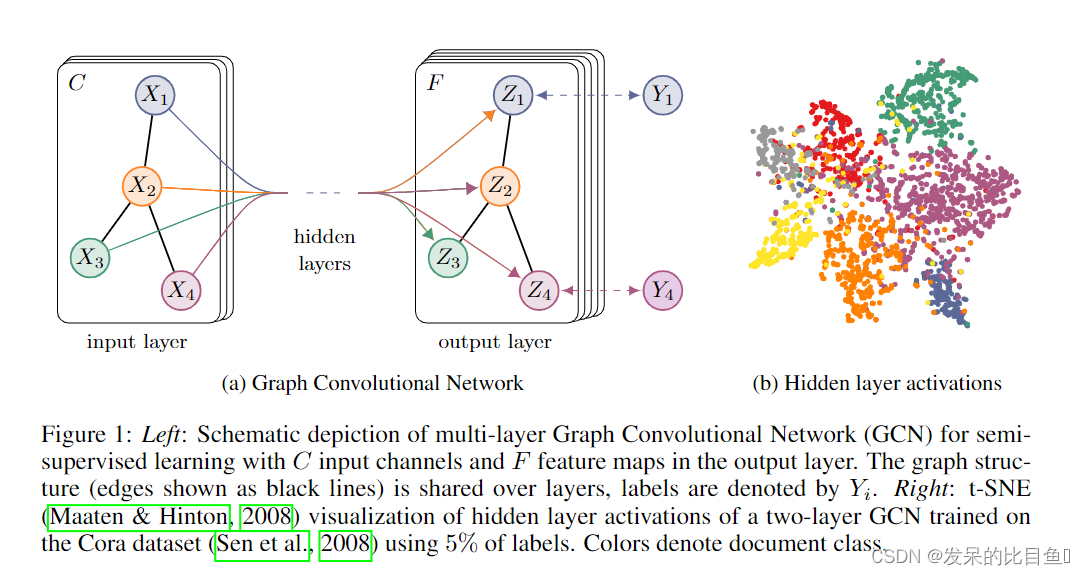
上图中,左(a)是一个GCN网络示意图,在输入层拥有CCC个输入,中间有若干隐藏层,在输出层有FFF个特征映射;图的结构(边用黑线表示)在层之间共享;标签用YiY_iYi表示。
右(b)是一个两层GCN在Cora数据集上(使用了5%的标签)训练得到的隐藏层激活值的形象化表示,颜色表示文档类别。
实验
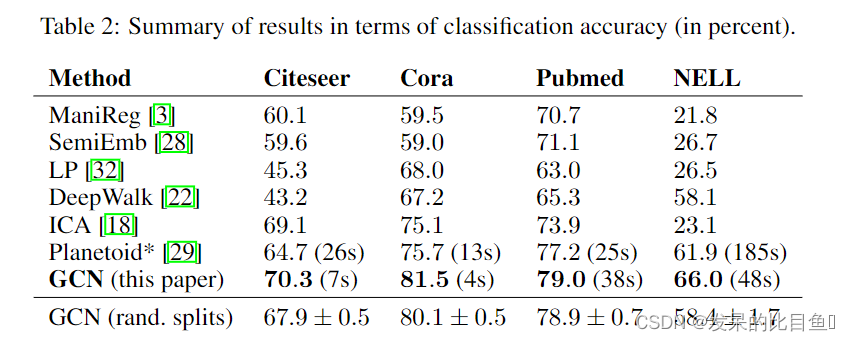









 该论文提出了图卷积网络(GCN)在处理图结构数据上的新方法,用于半监督学习。GCN通过图卷积实现节点特征的编码,模型在图的边数上线性扩展。作者探讨了傅里叶变换在图上的应用,以及如何利用拉普拉斯矩阵的特征向量进行图卷积。为了解决计算复杂性问题,引入了切比雪夫多项式近似,简化了卷积过程。实验表明,这种方法在引文网络和知识图数据集上显著优于现有技术,特别是在节点分类任务上。
该论文提出了图卷积网络(GCN)在处理图结构数据上的新方法,用于半监督学习。GCN通过图卷积实现节点特征的编码,模型在图的边数上线性扩展。作者探讨了傅里叶变换在图上的应用,以及如何利用拉普拉斯矩阵的特征向量进行图卷积。为了解决计算复杂性问题,引入了切比雪夫多项式近似,简化了卷积过程。实验表明,这种方法在引文网络和知识图数据集上显著优于现有技术,特别是在节点分类任务上。
















 1166
1166

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








