递归

递归：

（1）直接或间接的调用自身的算法
（2）使用函数自身给出的定义

1. 阶乘

循环实现阶乘
时间复杂度：O(n)
空间复杂度：S(1)

int fun(int n)
{
	int sum = 1;
	for(int i = 1; i <= n; ++i)
	{
		 sum = sum * i;
		 if(sum < 0) return -1;
	}
	return sum;
}

递归实现阶乘
时间复杂度：O(2^n)
空间复杂度：S(n)

int fan(int n)
{
	if(n <= 1)
		return 1;
	else
		return fan(n - 1) * n;
}

2. 斐波那契数列

递归实现斐波那契数列
时间复杂度：O(2^n)
空间复杂度：S(n)

int fun1(int n)
{
	if(n <= 2)
		return 1;
	if(n > 2)
		return fun1(n - 1) + fun1(n - 2);
}

循环实现斐波那契数列
时间复杂度：O(n)
空间复杂度：S(1)

int fan1(int n)
{
	int a = 1, b = 1, c = 1;
	for(int i = 3; i <= n; i++)
	{
		c = a + b;
		b = a;
		a = c;
	}
	return c;
}

3. 全排列

可参考 https://blog.youkuaiyun.com/hushhw/article/details/78112719
算法思路：
    (1) n 个元素的全排列 =（n-1 个元素的全排列）+（另一个元素作为前缀）；
    (2)出口：如果只有一个元素的全排列，则说明已经排完，则输出数组；
    (3)不断将每个元素放作第一个元素，然后将这个元素作为前缀，并将其余元素继续全排列，等到出口，出口出去后还需要还原数组；
如对1、2、3进行全排序
1 为前缀，对 2 和 3 进行排序，结果为 123、132。把 1 和 2 进行交换得到 2 1 3
2 为前缀，对 1 和 3 进行全排序，结果为 213、231。把 1 和 3 进行交换得到 3 2 1
3 为前缀，对 2 和 1 进行全排序，结果为 321、312。

void Perm(int *arr, int k, int m)
{
	if(k == m)
	{
		for(int i = 0; i <= m; ++i)
		{
			cout << arr[i] << " ";
		}
		cout<<endl;
	}
	else
	{
		for(int j =k; j <= m; j++)
		{
			swap(arr[j], arr[k]);
			Perm(arr, k + 1, m);
			swap(arr[j], arr[k]);
		}
	}
}

4. 数组的所有子集

数组 ar[ ] = {1，2，3}，其子集有
  ar[ ] = {1 2 3}
子集为0 0 0
           0 0 1
           0 1 1
           1 0 0
           1 0 1
           1 1 0
           1 1 1

void fun2(int *arr,int *brr,int i, int n)
 {
	 if(i >= n)
	 {
		 for(int j = 0;j < n; ++j)
		 {
			 if(brr[j])
			 {
				 cout<< arr[j]<< " ";
			 }
		 }
		 cout <<endl;
	 }
	 else
	 {
		 brr[i] = 1;
		 fun2(arr, brr, i+1, n);//left
		 brr[i] = 0;
		 fun2(arr, brr, i+1, n);//right
	 }
 }

5. 比较

比较递归中的 i+1，i++，++i，&i 的区别
（1）i+1
      第一次调用 fun(i+1, n), i+1，i本身的值没有变化，第二次调用 fun(i+1, n) 时，i本身的值没有变化，因此两次调用 fun(i, n) 时，i的值没有变化

 void fun3(int i, int n)
 {
	 if(i >= n)
	 {
		 cout <<i <<endl;
	 }
	 else
	 {
		 fun3(i+1, n);
		 fun3(i+1, n);
	 }
 }

（2）i++
       i是先调用 fun(i, n) 再进行 ++，但是之后调用的依旧是 fun(i, n)，而不是 fun(i++, n)，所以就陷入了死循环

void fun3(int i, int n)
 {
	 if(i >= n)
	 {
		 cout <<i <<endl;
	 }
	 else
	 {
		 fun3(i++, n);
		 fun3(i++, n);
	 }
 }

(3)++i
       调用 fun(i, n)，i 先进行 ++，再进行调用。下一次调用时，依旧是先 ++，再调用

 void fun3(int i, int n)
 {
	 if(i >= n)
	 {
		 cout <<i <<endl;
	 }
	 else
	 {
		 fun3(++i, n);
		 fun3(++i, n);
	 }
 }

（4）&i
       调用 fun(i, n)，i 先 ++，因为 i 被引用，所以，每次 ++ 之后前面调用的 i 的值就变成了 ++ 之后的值。

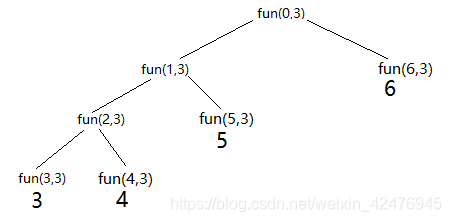
 void fun3(int &i, int n)
 {
	 if(i >= n)
	 {
		 cout <<i <<endl;
	 }
	 else
	 {
		 fun3(++i, n);
		 fun3(++i, n);
	 }
 }
int main()
{
	int i = 0, n = 3;
	fun3(i,n);
	return 0;
}

（5)&i,i+1
对 i 进行引用，要加 const 去常性
结果为 3 3 3 3 3 3 3 3

 void fun3(const int &i, int n)
 {
	 if(i >= n)
	 {
		 cout <<i <<endl;
	 }
	 else
	 {
		 fun3(i+1, n);
		 fun3(i+1, n);
	 }
 }