简单迭代法matlab例题程序_Java|写一个用迭代法解方程的Java程序

问题描述

迭代法也称辗转法，是一种逐次逼近方法，在使用迭代法解方程组时，其系数矩阵在计算过程中始终不变。它利用计算机运算速度快、适合做重复性操作的特点，让计算机对 一组指令 ( 或一定步骤 )进行重复执行，在每次执行这组指令(或步骤) 时，都从变量的原值推出它的一个新值。

迭代法具有循环的计算方法，方法简单，适宜解大型稀疏矩阵方程组，在用计算机计算时只需存储 A 的非零元素 (或可按一定公式形成系数，这样A就不需要存储)。

（1） 对于给定的方程组 X =Bx+f ，用式子 逐 步代入求近似解的方法称为迭代法( 或称为一阶定常迭代法 ,这里与B 和 k 无关 )

（2） 如果 limx (k) , x→∞ 存在 ( 记作 x* ), 称此迭代法收敛，显然 x就是方程组的解，否则称此迭代法发散。

解决方案

解法介绍

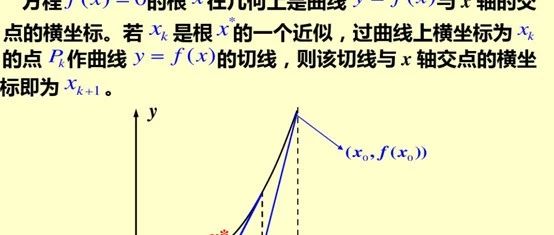
牛顿迭代法是一种线性化方法，其基本思想是将非线性方程 f(x)= 0逐步归结-为某种线性方程来求解.设已知方程f(x)=0有近似根X ( 假定 f’(x k )≠ 0), 将函数 f(x) 在点 x k 展开，有：

f(x)≈f(x k )+f’(x k )(x-x k ) 于是方程 f(x)=0 可近似地表示为 f(x)+ f’(x k )(x-x k )=0( 是个线性方程 ) ，记其根为 x k+1, 则 x k+1 的计算公式为 x k+1= x k -f(x k ) :heavy_division_sign: f’(x k ) （ k=0,1,2…… ）

例题讲解

例： 用牛顿迭代法三次求方程f(x)=x 5 -x 2 +x-30=0, 在区间 [1,3] 中的近似值请详细解答

解：

f (1)=-29

f(3)=207 所以 [1,3] 之间一定有零点。而且明显更靠近 x=3 。

f (2) =-2

f(2. 5)=63.9

f(2.2)=19.2

f(2.1)=8.53

f(2. 01)=0.78

f(2 001)=0.08

所以 f(2. 0001)=0.008 应该满足要求了。所以 x=2.0001

例：使用牛顿迭代法求方程的解， X 3 -2x-5=0 ，在区间 [2 ， 3]上的根。

package 
Lab_02.Test_01;

public class 
Test_01 {

public static void 
main(String[] args) {

double  x= 2
;

for ( int  i= 0 ;i< 20
;i++)  {

x=- f (x)/ f1 (x)+x;

}

out .println(x+ ""
);

}

static double  f( double  
x) {

double  ans;
ans=Math. pow (x,  3 )- 2 *x- 5
;

return  ans;
}

static double  f1( double  
x) {

double  ans;
ans= 3 *Math. pow (x,   2 )- 2
;

return  ans;
}

}

Java|写一个用迭代法解方程的Java程序​mp.weixin.qq.com