基于STM32F103的步进电机S型曲线加减速算法与实现

最新推荐文章于 2025-06-25 16:07:09 发布

༺༒至尊宝༒༻

最新推荐文章于 2025-06-25 16:07:09 发布

阅读量2.2w

点赞数 37

CC 4.0 BY-SA版权

分类专栏：电机算法文章标签：步进电机 S型加减速

本文链接：https://blog.youkuaiyun.com/weixin_42399752/article/details/85245942

步进电机是将电脉冲信号转变为角位移或线位移的开环控制电机，是现代数字程序控制系统中的主要执行元件，应用极为广泛。在非超载的情况下，电机的转速、停止的位置只取决于脉冲信号的频率和脉冲数，而不受负载变化的影响，当步进驱动器接收到一个脉冲信号，它就驱动步进电机按设定的方向转动一个固定的角度，称为“步距角”，它的旋转是以固定的角度一步一步运行的。可以通过控制脉冲个数来控制角位移量，从而达到准确定位的目的；同时可以通过控制脉冲频率来控制电机转动的速度和加速度，从而达到调速的目的。
步距角：对应一个脉冲信号，电机转子转过的角位移用θ表示。θ=360度/（转子齿数运行拍数），以常规二、四相，转子齿为50齿电机为例。四拍运行时步距角为θ=360度/（504）=1.8度（俗称整步），八拍运行时步距角为θ=360度/（50*8）=0.9度（俗称半步）。
转速(Rotational Speed或Rev)：是做圆周运动的物体单位时间内沿圆周绕圆心转过的圈数（与频率不同）。常见的转速有额定转速和最大转速等。
硬盘转速以每分钟多少转来表示，单位表示为RPM，RPM是Revolutions Per minute的缩写，是转/每分钟。RPM值越大，内部传输率就越快，访问时间就越短，硬盘的整体性能也就越好。
S型曲线的的方程：
y=1/(1+exp(-x));
x在［-5，5］的图形如下图所示：
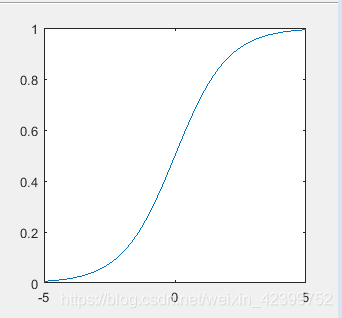
在这里插入图片描述
在Matlab软件中代码如下：

x=-5:0.01:5;
y=1./(1+exp(-x));
plot(x,y);

如要将此曲线应用在步进电机的加、减速过程中，需要将方程在XY坐标系进行平移，同时对曲线进行拉升变化：
Y=A+B/(1+exp(-ax+b));
其中的A分量在y方向进行平移，B分量在y方向进行拉伸，ax+b分量在x方向进行平移和拉伸。
其中的A分量在y方向进行平移，B分量在y方向进行拉伸，ax+b分量在x方向进行平移和拉伸。

项目中加速过程：从600Hz加速到20000Hz，采用4细分。输出比较模块所用的定时器驱动频率为10M，采用1000个点进行加速处理。最终根据项目的需要，在加速过程中采用的曲线方程为：
Fcurrent = Fmin + (Fmax-Fmin)/(1+exp( -flexible(i - num )/num) );*
步进电机S型曲线加减速算法与实现。

其中的Fcurrent为length（1000）个点中的单个频率值。Fmin起始频率为600; Fmax为最大频率20000; -flexible*（i - num）/num是对S型曲线进行拉伸变化，其中flexible代表S曲线区间（越大代表压缩的最厉害，中间（x坐标0点周围）加速度越大；越小越接近匀加速。理想的S曲