程序设计方法学（作业2）求两个正整数的最大公约数和最小公倍数

题目：求两个正整数的最大公约数和最小公倍数。
一、基本要求：
1.程序风格良好(使用自定义注释模板)，两种以上算法解决最大公约数问题，提供友好的输入输出。
二、提高要求：
1.三种以上算法解决两个正整数最大公约数问题。
2.求3个正整数的最大公约数和最小公倍数。
三、 算法的计算过程如下：
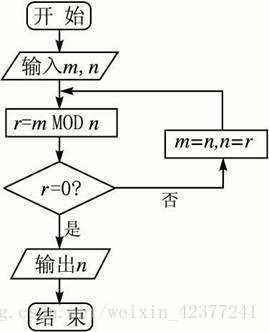
1.辗转相除法
辗转相除法基于如下原理：两个整数的最大公约数等于其中较小的数和两数的差的最大公约数。
辗转相除法的主要步骤是：
（1）用小的一个数除大的一个数，得第一个余数；
（2）用第一个余数除小的一个数，得第二个余数；
（3）用第二个余数除第一个余数，得第三个余数；
（4）逐次用后一个余数去除前一个余数，直到余数为0为止.

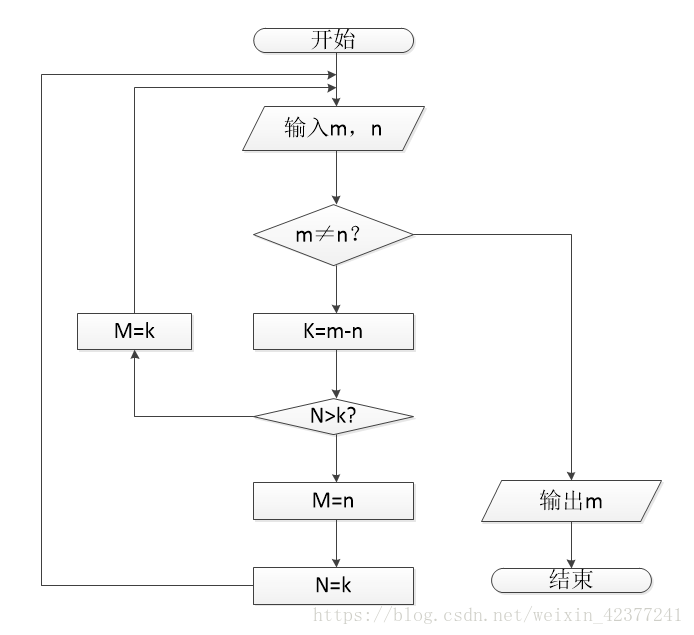
2.更相减损法
定义：更相减损法原本是为了约分而设计的：可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。
1.任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。
2.以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。
第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数，相当于不要第一步。

3.穷举法
穷举法即将所有的可能的结果从两数之中小的那个数开始，依次减1，然后带入进行验证是否满足被两数相除余数为0，若是找到符合的第一个数字，则即为最大公约数
4.所有具体的代码如下：

/////////////////////////////////////////////////////////////////////////////////////////////////////////