SG 理论学习笔记

SG 理论是博弈论中的另一个知识点，同样只作用于 ICG 游戏。

SG 理论也有地方说是 SG 函数，不过都是一个东西。

书接上回，这一篇我们继续探讨 ICG 游戏，所以请先阅读 博弈游戏学习笔记。

---

SG 函数用来解决一些很复杂的 ICG 游戏问题。

例如，有一个 ICG 游戏：Alice 和 Bob 正在一场组合游戏，这个游戏由 $7$ 个 DAG 博弈、$3$ 个 Bash 博弈、$7$ 个威佐夫博弈、$4$ 个斐波那契博弈……组成。

（不管有多少个游戏，只要这个东西是 ICG 游戏就行）

规则：每一次行动可以选择其中一个游戏，进行一次行动，如果不能行动就算输。

这是什么啊？？？你给我单个博弈游戏还可以，但是这堆东西组合起来是什么东西？？

考虑突破点：我们知道，任何一个 ICG 游戏，都可以转化为一个 DAG 上面的游戏。

这个是很显而易见的，如果你阅读完了我上一篇文章的话。

那么所有游戏就都变成了一个 DAG 博弈。整个游戏相当于在一个 DAG 森林上面的博弈。

假设我们目前面临着一个 DAG 游戏。

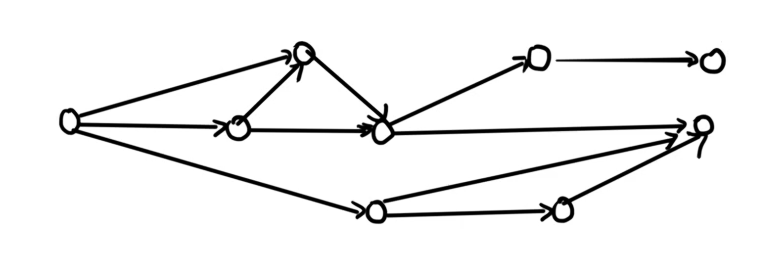
显然可以快速地判断是 N 态还是 P 态。

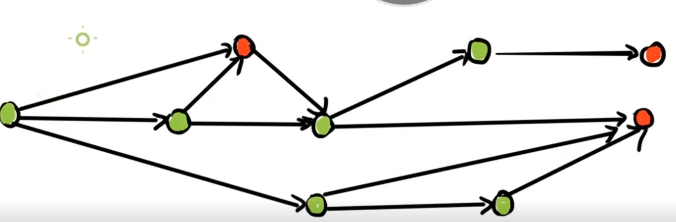
但是注意这是一个 DAG 森林，不能再只使用 NP 态来描写这个局面了。

---

考虑对于每一个结点都赋予一个特殊的值。

不妨使用 $dp$ 来表示（因为 NP 态的转移本质上也可以说是一种动态规划）：对于 $u$，枚举它所有可以连向的点 $v$，令 dpu=mex{dpv}dp_u = \text{mex}\{dp_v\}dpu​=mex{dpv​}。

插叙一句：$\text{mex}$ 这个运算符很重要，它是指集合中没有出现的最小的自然数。例如 {0,1,2}\{0,1,2\}{0,1,2} 的 $\text{mex}$ 是 $3$，{1,2,3}\{1,2,3\}{1,2,3} 的 $\text{mex}$ 是 $0$，而 {0,1,3,4}\{0,1,3,4\}{0,1,3,4} 的 $\text{mex}$ 是 $2$。

特殊地，如果 $u$ 没有可以连向的结点，则 $d{p}_u=0$。

很容易可以得出所有点的 $dp$ 值。

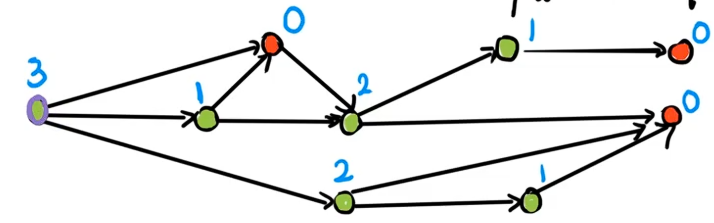
那么这个东西又有什么用呢？？？

---

其实是这样的，单个 DAG 博弈的过程，可以看成一个在 $dp$ 上面取石子的过程。

为什么这么说呢？因为 $\text{mex}$ 有一个很友好的特点：小于 $d{p}_u$ 值在 $d{p}_v$ 里面一定出现了，其中 $v$ 表示 $u$ 所有连向的点。

所以 $d{p}_u$ 到达小于 $d{p}_u$ 的 $d{p}_v$ 的时候就相当于取石子了。

显然不存在 $d{p}_u=d{p}_v$，因为它是 $\text{mex}$，显然不可能在连向的结点中出现同样的值。所以不会存在不取石子的情况。

你会问：当 $d{p}_v>d{p}_u$ 怎么办呢？？？注意，我们的后手可以再次运用结论，使用还原思想。

因为 $d{p}_v>d{p}_u$，所以在 $v$ 连向的结点 $w$ 中，也一定存在 $d{p}_w=d{p}_u$（因为小于 $d{p}_v$ 的值在所有 $d{p}_w$ 中都一定会出现最少一次）。所以后手又可以通过还原将 $d{p}_u\to d{p}_v$ 变大的行为忽略。

于是，这样的一个整个的 DAG 就相当于一个取石子游戏了。

注意，由于每一个游戏的起始点只有一个，所以石子堆的石子数量就是起始点的 $dp$ 值。

对于这个 $dp$ 值，就叫做 SG 值。也可以说是 SG 函数。

---

考虑再回到原来的问题。我们说过每一个游戏都能变成一个 DAG，然而每一个 DAG 又可以变成一个石子堆。

那不就是一个 Nim 游戏了吗？？？

显然根据结论，如果所有游戏的 $SG$ 值的异或不是 $0$，则它是一个 $N$ 态，则先手必胜。如果 $SG$ 值的异或 $=0$，则它是一个 $P$ 态。

考虑具体的 $N$ 态怎么实现必胜策略：

• 首先，先手让异或和为 $0$。

• 接下来有两种情况：

  • 1.后手选择增加其中一个值，先手选择还原。（这个操作次数虽然有限，但是后手能走先手就一定能走）

  • 2.后手选择降低其中一个值，先手正常按 Nim 的必胜策略来操作。

注意一下，Nim 游戏的 SG 值就是它们所有石子堆的异或和。

如何计算 SG

这个才是 SG 函数的难点：$\text{mex}$ 是什么啊？？如何计算？

首先，我们可以先建 DAG 图之后暴力计算。（暴力计算）

此外，还有两种方法：

• 1.找到数学规律，给出 SG 的计算式子/递推式子（数学分析）

• 2.打表找规律。

CF15C Industrial Nim

显然这个游戏是一个 Nim 套 Nim。

根据我们前面说的，Nim 的 SG 函数 就是所有石子堆数量的异或和。

也就是说要判断这个东西是不是 $=0$：

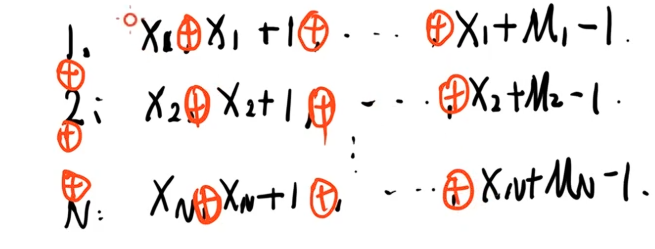
因为 $[x_i,x_i+m_i+1]$ 构成了一个个区间，所以问题变成了如何求区间的异或和。

显然可以使用前缀异或和，即计算 $[L,R]$ 的异或和相当于 $[1,L-1]$ 的异或和异或上 $[1,R]$ 的异或和。

---

问题就变成了如何计算 $[1,x]$ 的异或和。

考虑打表找规律。设 $f(i)$ 表示 $[1,i]$ 的异或和。

$i$	$f(i)$
1	1
2	3
3	0
4	4
5	1
6	7
7	0
8	8
9	1
10	11
11	0
12	12
13	1

我们发现，这东西有规律！

当 $i=4k+1$ 的时候，$f(i)=1$。

当 $i=4k+2$ 的时候，$f(i)=i+1$。

当 $i=4k+3$ 的时候，$f(i)=0$。

当 $i=4k$ 的时候，$f(i)=i$。

---

于是我们就找到了规律，就可以求解这道题目了。分类讨论即可。

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n;

int get(int x) {
	if (x % 4 == 0)
		return x;
	else if (x % 4 == 1)
		return 1;
	else if (x % 4 == 2)
		return x + 1;
	else
		return 0;
}

signed main() {
	cin >> n;
	int x = 0;
	while (n--) {
		int a, b;
		cin >> a >> b;
		b = a + b - 1;
		x ^= get(b)^get(a - 1);
	}
	if (x)
		cout << "tolik\n";
	else
		cout << "bolik\n";
	return 0;
}