数据分析-65-全面解析伦敦共享单车使用规律（包含代码和数据）_本研究通过深入分析伦敦共享单车使用行程数据集,重点关注骑行高峰期、站点流量、-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_42363541/article/details/143210941

算法学习、4对1辅导、论文辅导、核心期刊
项目的代码和数据下载可以通过公众号滴滴我

文章目录

一、项目背景

随着共享单车在全球范围内的普及，城市交通出行模式发生了巨大变化。伦敦作为国际化大都市，交通拥堵问题日益严重，共享单车作为一种绿色、环保、便捷的出行方式，逐渐成为解决交通问题的重要组成部分，然而，要实现共享单车系统的高效运营，必须深入了解用户的使用习惯和需求。本项目对伦敦共享单车数据进行了全面分析，涵盖了数据清洗、特征工程（构建新特征）、骑行高峰期分析、站点流量分析，以及通过聚类分析将800个站点划分为5类，并对每一类站点提出建议，最后通过方差分析探讨了影响共享单车流量的因素，通过这些步骤，可以识别高频使用的时间段和站点，为运营商提供优化调度和资源分配的科学依据。

二、数据说明

该数据共77万+条数据，共11个字段。分别是

列名	说明
Number	每次出行的唯一标识符（Trip ID）
Start Date	出行开始的日期和时间
Start Station Number	起始站的标识符
Start Station	起始站的名称
End Date	出行结束的日期和时间
End Station Number	终点站的标识符
End Station	终点站的名称
Bike Number	所使用自行车的唯一标识符
Bike Model	所使用自行车的型号
Total Duration	出行的总时间（时分秒）
Total Duration (ms)	出行的总时间（毫秒）

下面是表的部分数据
在这里插入图片描述

三、数据处理

1、导入包以及数据读取

导入包

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import networkx as nx
import matplotlib.colors as mcolors
import numpy as np
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score
import scipy.stats as stats
import warnings
warnings.filterwarnings('ignore')
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

设置Matplotlib的中文字体显示

from pylab import mpl    
mpl.rcParams["font.sans-serif"] = ["SimHei"] # 设置显示中文字体 宋体    
mpl.rcParams["axes.unicode_minus"] = False #字体更改后，会导致坐标轴中的部分字符无法正常显示，此时需要设置正常显示负号

读取数据

data = pd.read_csv('LondonBikeJourneyAug2023.csv')

2、数据预览以及数据处理

查看数据维度

# 查看数据维度
data.shape

(776527, 11)

查看数据信息

#查看数据信息
data.info()

在这里插入图片描述

查看各列缺失值

#查看各列缺失值
data.isna().sum()

在这里插入图片描述

查看重复值

#查看重复值
data.duplicated().sum()

将起始日期和结束日期转换为日期时间格式

# 将起始日期和结束日期转换为日期时间格式
data['Start date'] = pd.to_datetime(data['Start date'])
data['End date'] = pd.to_datetime(data['End date'])

获取数据集中最早和最晚的日期

# 获取数据集中最早和最晚的日期
start_date_min = data['Start date'].min()
start_date_max = data['Start date'].max()
end_date_min = data['End date'].min()
end_date_max = data['End date'].max()

print(f"数据集中最早的起始日期: {start_date_min}")
print(f"数据集中最晚的起始日期: {start_date_max}")
print(f"数据集中最早的结束日期: {end_date_min}")
print(f"数据集中最晚的结束日期: {end_date_max}")

数据集中最早的起始日期: 2023-08-01 00:00:00
数据集中最晚的起始日期: 2023-08-31 23:59:00
数据集中最早的结束日期: 2023-08-01 00:04:00
数据集中最晚的结束日期: 2023-11-09 20:19:00

总结：发现起止的时间对不起来，这里直接删除出行结束的日期和时间，因为的打算从开始骑行的时间入手（做流量分析，肯定是分析开始骑行的时间）。

data.drop(['End date'],axis=1,inplace=True)

# 获取起始站和终点站
start_stations = data['Start station'].value_counts()
end_stations = data['End station'].value_counts()
print(f'起始站数量:{len(start_stations)},终点站数量:{len(end_stations)}')

起始站数量:800,终点站数量:802

总结：很奇怪，正常来说，起始站和终点站的数量应该一致才对，这里进一步分析，看看仅作为终点站的数据占比是否大，如果不大的话，就怀疑是异常数据。

# 查看起点站点和终点站点的差异
unique_start_stations = set(start_stations.index)
unique_end_stations = set(end_stations.index)
# 终点站点但不是起点站点
only_end_stations = unique_end_stations - unique_start_stations
for station in only_end_stations:
    print(f"{station}: {end_stations[station]} 次")

Mechanical Workshop Clapham: 30 次
Mechanical Workshop Penton: 5 次

总结：发现以这两个站作为终点站的次数为35次，这对于70多万条数据来说，可以忽略不计了，这里直接删除吧。

# 删除这些站点的数据
stations_to_remove = list(only_end_stations)
data = data[~data['Start station'].isin(stations_to_remove)]
data = data[~data['End station'].isin(stations_to_remove)]

# 删除起始点和终点站是同一个地方的数据
data = data[data['Start station'] != data['End station']]

plt.figure(figsize=(16,8))
sns.boxplot(y=data['Total duration (ms)'])
plt.title('骑行时长分布情况')
plt.ylabel('骑行时长（毫秒）')
plt.show()

在这里插入图片描述

总结：Total duration (ms)这个特征异常值有点多，打算直接用Total duration这个特征转为以“秒”为基本单位的骑行总时长。

data.drop(['Total duration (ms)'],axis=1,inplace=True)

def convert_duration_to_seconds(duration_str):
    time_parts = duration_str.split()
    total_seconds = 0

    for part in time_parts:
        if 'h' in part:
            total_seconds += int(part.replace('h', '')) * 3600
        elif 'm' in part:
            total_seconds += int(part.replace('m', '')) * 60
        elif 's' in part:
            total_seconds += int(part.replace('s', ''))

    return total_seconds

data['Total duration (s)'] = data['Total duration'].apply(convert_duration_to_seconds)

plt.figure(figsize=(16,8))
sns.boxplot(y=data['Total duration (s)'])
plt.title('骑行时长分布情况')
plt.ylabel('骑行时长（秒）')
plt.show()

在这里插入图片描述

总结：发现还是存在大量异常值，8万多秒，大约是22小时多，正常来说，应该没人会用共享单车骑行那么久吧……这里直接设置一个上限，骑行8小时（8小时等于28800秒），下限1分钟（我认为，如果小于1分钟很可能是异常数据，或者此次没有出现）。

max_duration = 8 * 3600  # 8小时（28800秒）
min_duration = 60
# 标记并删除异常值
data = data[(data['Total duration (s)'] >= min_duration) & (data['Total duration (s)'] <= max_duration)].copy()

# 构建新特征
data['date'] = data['Start date'].dt.date # 骑行日期
data['hour'] = data['Start date'].dt.hour
data['weekday'] = data['Start date'].dt.day_name()

data.head()

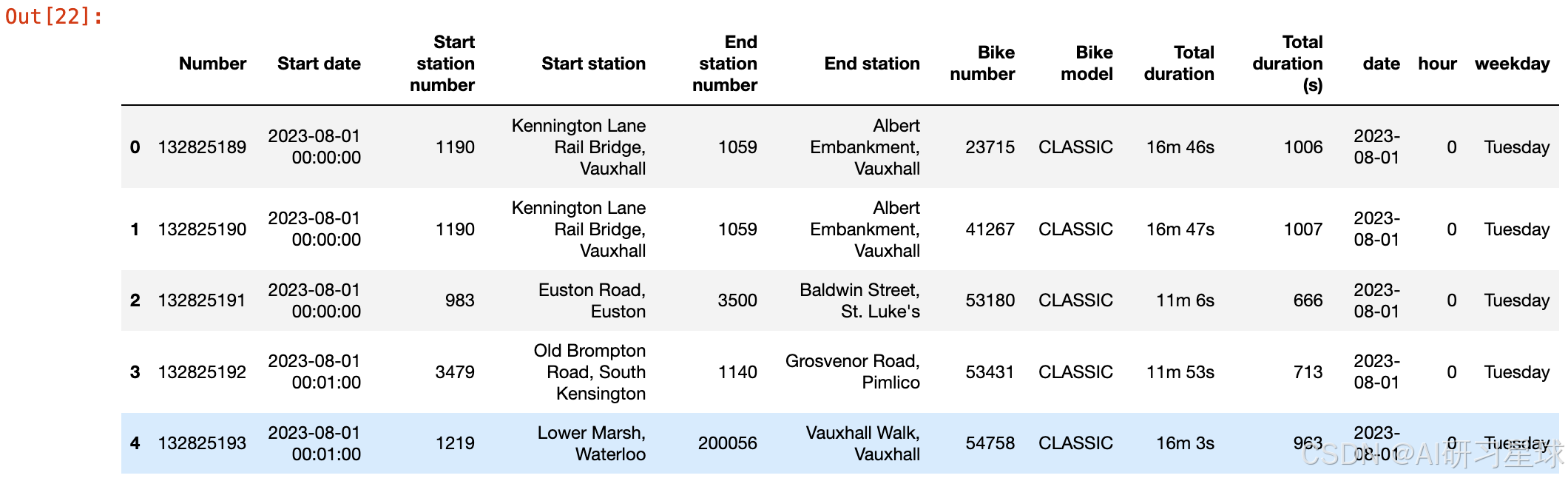
在这里插入图片描述

3、描述性分析

data.describe(include='all')

在这里插入图片描述

4、骑车高峰期分析

a、八月骑行情况分析

# 计算每天的骑行总时长和骑行次数
daily_stats = data.groupby('date').agg({'Total duration (s)': 'sum', 'Number': 'count'}).reset_index()
daily_stats.rename(columns={'Number': 'Ride Count'}, inplace=True)
# 创建双 y 轴图表
fig, ax1 = plt.subplots(figsize=(12, 6))
# 绘制总时长
color = 'tab:blue'
ax1.set_xlabel('日期')
ax1.set_ylabel('骑行总时长（秒）', color=color)
ax1.plot(daily_stats['date'], daily_stats['Total duration (s)'], color=color, marker='o', label='总时长')
ax1.tick_params(axis='y', labelcolor=color)

# 创建第二个 y 轴，共享 x 轴
ax2 = ax1.twinx()
color = 'tab:orange'
ax2.set_ylabel('骑行次数', color=color)
ax2.plot(daily_stats['date'], daily_stats['Ride Count'], color=color, marker='x', label='骑行次数')
ax2.tick_params(axis='y', labelcolor=color)

# 添加图例
fig.tight_layout()
fig.legend(loc='upper right', bbox_to_anchor=(0.94,0.95))

plt.title('每天的骑行总时长和骑行次数')
plt.show()

在这里插入图片描述
总结：观察时序图，可以发现，当天骑行次数与总时长的变化相对一致，说明大多数情况下，骑行的平均时长大体相同，但是可以看到还是有几个日期（8月13日、8月14日等）出现了骑行次数减少，而总时长是上升的，这是因为在这些日期中骑行的平均时长可能有所不同；骑行总时长和骑行次数在整个8月中有显著的波动，表明共享单车的使用量在不同的日期有很大变化，这种波动性可能与天气、节假日、工作日等因素有关，8月5日是显著的低谷期，与前后两天的骑行流量成鲜明的对比。

b、每周每天骑行情况分析

plt.figure(figsize=(20,6))
weekday_rides = data.groupby('weekday').size()
plt.subplot(1,2,1)
sns.barplot(x=weekday_rides.index, y=weekday_rides.values, order=['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday'])
plt.title('每周每天的骑行次数')
plt.xlabel('星期')
plt.ylabel('骑行次数')

weekday_duration = data.groupby('weekday')['Total duration (s)'].sum().reset_index()
weekday_duration['weekday'] = pd.Categorical(weekday_duration['weekday'], categories=['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday'], ordered=True)
weekday_duration = weekday_duration.sort_values('weekday')
plt.subplot(1,2,2)
sns.barplot(data=weekday_duration, x='weekday', y='Total duration (s)')
plt.title('每周每天的骑行总时长')
plt.xlabel('星期')
plt.ylabel('骑行总时长（秒）')
plt.tight_layout()
plt.show()

在这里插入图片描述
总结：周二、周三、周四都是共享单车的高峰期，无论是次数还是总时长都远远高于其他时候；而周六是低谷期，骑行次数和总时长都比较短；周天的骑行次数虽然不多，但是总时长比较长，说明平均骑行时长远远高于周一和周五。

c、每天高峰期时段分析

plt.figure(figsize=(12, 6))
hourly_rides = data.groupby('hour').size()
hourly_rides.plot(kind='bar')
plt.title('每小时的骑行次数')
plt.xlabel('小时')
plt.ylabel('骑行次数')
plt.xticks(rotation=0)
plt.show()

在这里插入图片描述
总结：每天的共享单车高峰期是8点、17点和18点这个时间段，这段时间正好是人们上下班的高峰期，因此作为共享单车的管理者，应当合理分配单车的维护时间，可以把维护时间放在20点以后，然后要保证两段高峰期的用车情况。

5、站点流量分析

a、基于热门路线分析

# 统计站点间的骑行次数
station_flows = data.groupby(['Start station', 'End station']).size().reset_index(name='ride_counts')

# 创建一个字典来存储站点对的权重
flow_dict = {}
for index, row in station_flows.iterrows():
    start, end, count = row['Start station'], row['End station'], row['ride_counts']
    if (start, end) in flow_dict:
        flow_dict[(start, end)] += count
    else:
        flow_dict[(start, end)] = count

# 将字典转换回DataFrame
station_flows['weight'] = station_flows.apply(lambda row: flow_dict[(row['Start station'], row['End station'])], axis=1)

# 选择前10条常用的站点路线
top_station_flows = station_flows.sort_values(by='weight', ascending=False).head(10)

# 提取前10条路线中的所有站点
top_stations = set(top_station_flows['Start station']).union(set(top_station_flows['End station']))

# 过滤数据，只保留前10条路线中的站点
filtered_flows = station_flows[(station_flows['Start station'].isin(top_stations)) & (station_flows['End station'].isin(top_stations))]

top_station_flows

在这里插入图片描述
总结：这里获取了最热门的10条线路，这些数据表明，热门线路大多集中在公园和旅游景点附近，可能与游客和居民的出行需求有关。

top_stations

在这里插入图片描述
总结：可以看到常用的前10条线路中，有8个站点，继续对这8个站点进行分析。

# 创建一个有向图
G = nx.DiGraph()

# 添加边和权重（骑行次数）
for index, row in filtered_flows.iterrows():
    start_station = row['Start station']
    end_station = row['End station']
    weight = row['weight']
    G.add_edge(start_station, end_station, weight=weight)

plt.figure(figsize=(15,10))

# 使用circular_layout布局
pos = nx.circular_layout(G)

# 绘制节点
nx.draw_networkx_nodes(G, pos, node_size=700, node_color='skyblue')

# 获取所有颜色
colors = list(mcolors.CSS4_COLORS.values())
np.random.shuffle(colors)

# 绘制边，双向边不显示箭头，自环边显示箭头
edges = G.edges(data=True)
for i, (u, v, d) in enumerate(edges):
    nx.draw_networkx_edges(G, pos, edgelist=[(u, v)], arrowstyle='-', arrowsize=10, edge_color=colors[i % len(colors)], width=2)

# 绘制节点标签
nx.draw_networkx_labels(G, pos, font_size=10, font_family='sans-serif')

# 绘制边标签
edge_labels = {(u, v): d['weight'] for u, v, d in G.edges(data=True)}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)

plt.title('前10条常用站点路线的流量网络图')
plt.show()

在这里插入图片描述

总结：Hyde Park Corner, Hyde Park是最主要的枢纽站点，从该站点出发或到达的骑行次数最多，Albert Gate, Hyde Park和Black Lion Gate, Kensington Gardens也是重要的枢纽站点，连接了多个骑行路线，这些高流量线路主要集中在Hyde Park及其周边区域，显示出这些区域的高需求。Ackroyd Drive, Bow和Maplin Street, Mile End之间的骑行次数虽然较少，但仍是热门线路，毕竟排在前十，Hyde Park Corner, Hyde Park是最重要的枢纽站点，连接了多个高流量线路。运营者可以在这些站点增加自行车数量，以满足高需求。

b、基于起始站分析

# 统计每个站点作为起始站和终点站每天的骑行次数
daily_start_rides = data.groupby(['Start station', 'date']).size().reset_index(name='start_ride_counts')
daily_end_rides = data.groupby(['End station', 'date']).size().reset_index(name='end_ride_counts')

# 计算每个站点的平均每天骑行次数
avg_daily_start_rides = daily_start_rides.groupby('Start station')['start_ride_counts'].mean().reset_index()
avg_daily_start_rides.columns = ['Station', 'Avg Daily Start Rides']

# 找到排名前10的起始站，如果有并列第十名的情况，全部绘制
top_10_avg_rides = avg_daily_start_rides[avg_daily_start_rides['Avg Daily Start Rides'] >= avg_daily_start_rides['Avg Daily Start Rides'].nlargest(10).min()]

# 对结果进行排序
top_10_avg_rides = top_10_avg_rides.sort_values(by='Avg Daily Start Rides', ascending=False)

# 绘制条形图
plt.figure(figsize=(12,8))
plt.barh(top_10_avg_rides['Station'], top_10_avg_rides['Avg Daily Start Rides'], color='skyblue')
plt.xlabel('平均每天骑行次数')
plt.ylabel('起始站')
plt.title('排名前10的起始站（按平均每天骑行次数）')
plt.gca().invert_yaxis()  # 反转y轴，使得排名靠前的在上方
plt.show()

在这里插入图片描述
总结：与之前分析的一致：Hyde Park Corner, Hyde Park是最热门的起始站，平均每天有大约140次骑行，这个站点显然是一个重要的枢纽。
图中的多个站点都位于Hyde Park、Waterloo和Liverpool Street周边，这些区域显然是骑行活动的集中地。可能是因为这些区域是商业中心、交通枢纽或者旅游景点，吸引了大量的自行车使用者，运营者应在Hyde Park Corner,Hyde Park和Waterloo区域内增加更多的自行车和停车设施，以满足高需求。

# 找到排名倒数10的起始站，如果有并列第八十名的情况，全部绘制
bottom_10_avg_rides = avg_daily_start_rides[avg_daily_start_rides['Avg Daily Start Rides'] <= avg_daily_start_rides['Avg Daily Start Rides'].nsmallest(10).max()]

# 对结果进行排序
bottom_10_avg_rides = bottom_10_avg_rides.sort_values(by='Avg Daily Start Rides')

# 绘制条形图
plt.figure(figsize=(12,8))
plt.barh(bottom_10_avg_rides['Station'], bottom_10_avg_rides['Avg Daily Start Rides'], color='lightcoral')
plt.xlabel('平均每天骑行次数')
plt.ylabel('起始站')
plt.title('排名倒数10的起始站（按平均每天骑行次数）')
plt.gca().invert_yaxis()  # 反转y轴，使得排名靠前的在上方
plt.show()

在这里插入图片描述

总结：这些低频使用站点主要分布在奥林匹克公园、汉默史密斯、帕特尼、坎纳里码头和拉德布鲁克格罗夫等区域，可能位于城市的边缘地带、居民区或并非商业和旅游中心，导致骑行需求较低，运营者可以考虑在这些低频使用站点减少自行车和停车设施，以节约资源，将更多的自行车和设施部署到高需求区域，提高运营效率，尽管这些站点目前骑行需求较低，但可以进一步分析这些区域的潜在需求，通过用户调查和反馈了解这些低频站点的使用情况和问题。还可以通过推广和活动，增加这些区域的骑行使用率，例如在社区内组织骑行活动或提供优惠。

c、站点净流量分析

净流量（Net Flow）在共享单车分析中通常表示一个站点的出站和入站之间的差异。具体来说，净流量可以定义为一个站点在一段时间内的起点骑行次数减去终点骑行次数。净流量的正值表示该站点有更多的骑行是从这里开始的，而净流量的负值表示该站点有更多的骑行是到这里结束的。

avg_daily_end_rides = daily_end_rides.groupby('End station')['end_ride_counts'].mean().reset_index()
avg_daily_end_rides.columns = ['Station', 'Avg Daily End Rides']

# 合并数据，计算差值
avg_daily_rides = pd.merge(avg_daily_start_rides, avg_daily_end_rides, on='Station', how='outer').fillna(0)
avg_daily_rides['avg_ride_diff'] = avg_daily_rides['Avg Daily Start Rides'] - avg_daily_rides['Avg Daily End Rides']

# 找到前十和倒数十的站点
top_10_diff = avg_daily_rides.nlargest(10, 'avg_ride_diff')
bottom_10_diff = avg_daily_rides.nsmallest(10, 'avg_ride_diff')
# 对前十和倒数十的站点分别进行排序
top_10_diff = top_10_diff.sort_values(by='avg_ride_diff', ascending=False)
bottom_10_diff = bottom_10_diff.sort_values(by='avg_ride_diff', ascending=False)

# 合并前十和倒数十的站点数据
combined_diff = pd.concat([top_10_diff, bottom_10_diff])

# 设置颜色
colors = ['skyblue' if x >= 0 else 'lightcoral' for x in combined_diff['avg_ride_diff']]

# 绘制条形图
plt.figure(figsize=(14, 10))
plt.barh(combined_diff['Station'], combined_diff['avg_ride_diff'], color=colors)
plt.xlabel('站点净流量')
plt.ylabel('站点')
plt.title('前十和倒数十站点（站点净流量）')
plt.axvline(0, color='black', linewidth=0.8)
plt.gca().invert_yaxis()  # 反转y轴，使得正x轴的在上方
plt.show()

在这里插入图片描述
总结：
高净流量站点：需要增加自行车供应，以满足高需求。
低净流量站点：需要增加停车设施，以接纳更多到达的自行车。
根据净流量调整自行车的调度和分布策略，确保高需求站点有足够的自行车供应，低需求站点有足够的停车位。
通过优化资源分配和运营策略，提高用户的使用体验，减少在高需求站点找不到自行车或低需求站点没有停车位的问题。

d、基于K-Means聚类分析

station_stats = pd.merge(avg_daily_start_rides, avg_daily_end_rides, on='Station', how='outer').fillna(0)# 计算每天平均骑行次数差值
station_stats['Avg Daily Ride Diff'] = station_stats['Avg Daily Start Rides'] - station_stats['Avg Daily End Rides']
# 计算每个站点骑行的平均时长
start_duration = data.groupby('Start station')['Total duration (s)'].mean().reset_index()
start_duration.columns = ['Station', 'Avg Ride Duration']
station_stats = pd.merge(station_stats, start_duration, on='Station', how='outer').fillna(0)

station_stats.head()

在这里插入图片描述

features = station_stats.drop(['Station'],axis=1)
# 数据标准化
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# 使用肘部法则来确定最佳聚类数
inertia = []
silhouette_scores = []
k_range = range(2, 11)
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=15,n_init=10).fit(scaled_features)
    inertia.append(kmeans.inertia_)
    silhouette_scores.append(silhouette_score(scaled_features, kmeans.labels_))

plt.figure(figsize=(15,5))

plt.subplot(1, 2, 1)
plt.plot(k_range, inertia, marker='o')
plt.xlabel('聚类中心数目')
plt.ylabel('惯性')
plt.title('肘部法则图')

plt.subplot(1, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o')
plt.xlabel('聚类中心数目')
plt.ylabel('轮廓系数')
plt.title('轮廓系数图')

plt.tight_layout()
plt.show()

在这里插入图片描述
总结：通过肘部法则图观察到 k=5 到 k=6 之间的下降变化开始减少。通过轮廓系数图观察到轮廓系数在 k=2 时最高，之后随着聚类数的增加而逐渐降低。二者结合：根据轮廓系数，尽管 k=2 时得分最高，但考虑到肘部法则的结果，我们可能更倾向于选择 k=5,因为它提供了更合理的聚类数量和较好的聚类质量。

# 使用 K-means 进行聚类
kmeans = KMeans(n_clusters=5, random_state=15,n_init=10)
kmeans.fit(scaled_features)
labels = kmeans.labels_
station_stats['Cluster'] = kmeans.labels_

# 使用 PCA 将数据降维到 2 维以便可视化
pca = PCA(n_components=2)
reduced_features = pca.fit_transform(scaled_features)

# 可视化聚类结果
plt.figure(figsize=(12, 8))
plt.scatter(reduced_features[:, 0], reduced_features[:, 1], c=labels, cmap='viridis', marker='o')
centers = kmeans.cluster_centers_
reduced_centers = pca.transform(centers)
plt.scatter(reduced_centers[:, 0], reduced_centers[:, 1], c='red', s=200, alpha=0.75, marker='x')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('站点聚类结果')
plt.show()

在这里插入图片描述

# 计算每个聚类的特征均值和标准差
cluster_summary = station_stats.groupby('Cluster').agg({
    'Avg Daily Start Rides': ['mean', 'std'],
    'Avg Daily End Rides': ['mean', 'std'],
    'Avg Daily Ride Diff': ['mean', 'std'],
    'Avg Ride Duration': ['mean', 'std'],
}).reset_index()

print(cluster_summary)

在这里插入图片描述

# 可视化对比
plt.figure(figsize=(20,15))
plt.subplot(2,2,1)
sns.boxplot(x='Cluster', y='Avg Daily Start Rides', data=station_stats, palette='viridis')
plt.xlabel('聚类')
plt.ylabel('每天平均起始次数')
plt.title('不同聚类中的每天平均起始次数分布')

plt.subplot(2,2,2)
sns.boxplot(x='Cluster', y='Avg Daily End Rides', data=station_stats, palette='viridis')
plt.xlabel('聚类')
plt.ylabel('每天平均终点次数')
plt.title('不同聚类中的每天平均终点次数分布')

plt.subplot(2,2,3)
sns.boxplot(x='Cluster', y='Avg Daily Ride Diff', data=station_stats, palette='viridis')
plt.xlabel('聚类')
plt.ylabel('每天平均骑行次数差值（净流量）')
plt.title('不同聚类中的每天平均骑行次数差值（净流量）分布')

plt.subplot(2,2,4)
sns.boxplot(x='Cluster', y='Avg Ride Duration', data=station_stats, palette='viridis')
plt.xlabel('聚类')
plt.ylabel('平均骑行时长（秒）')
plt.title('不同聚类中的平均骑行时长分布')

plt.tight_layout()
plt.show()

在这里插入图片描述
总结：

聚类 0

特征描述：
- 每天平均起始次数: 平均 21.17 次，标准差 6.48
- 每天平均终点次数: 平均 20.40 次，标准差 6.49
- 每天平均骑行次数差值（净流量）: 平均 0.78 次，标准差 1.91
- 平均骑行时长: 平均 975 秒，标准差 114 秒
情况划分：
- 使用频率较低：每天平均起始次数和终点次数较低，表明这些站点使用频率较低。
- 使用平衡：净流量较小，起始次数和终点次数接近，表明这些站点的使用较为均衡。
- 短途骑行：骑行时长较短，可能主要用于短途出行。
建议：
- 优化资源配置：由于使用频率较低，建议优化这些站点的自行车资源配置，减少闲置车辆。
- 推广和宣传：加强这些站点周边的推广和宣传，吸引更多用户使用，提高使用频率。

聚类 1

特征描述：
- 每天平均起始次数: 平均 72.32 次，标准差 18.32
- 每天平均终点次数: 平均 74.80 次，标准差 18.19
- 每天平均骑行次数差值（净流量）: 平均 -2.48 次，标准差 4.38
- 平均骑行时长: 平均 1342 秒，标准差 399 秒
情况划分：
- 使用频率较高：每天平均起始次数和终点次数较高，表明这些站点使用频率较高。
- 终点站使用更多：净流量为负，终点次数略高于起始次数，表明这些站点更常作为终点站使用。
- 长途骑行：骑行时长较长，可能是一些长途出行的主要站点。
建议：
- 增加自行车停放设施：由于终点站使用更多，建议增加这些站点的自行车停放设施，避免高峰期车辆积压。
- 优化调度：加强这些站点的车辆调度，确保在高峰期能够满足需求，尤其是将车辆调度到起始站。

聚类 2

特征描述：
- 每天平均起始次数: 平均 41.59 次，标准差 8.08
- 每天平均终点次数: 平均 40.98 次，标准差 7.72
- 每天平均骑行次数差值（净流量）: 平均 0.61 次，标准差 4.23
- 平均骑行时长: 平均 983 秒，标准差 138 秒
情况划分：
- 使用频率中等：每天平均起始次数和终点次数中等，表明这些站点使用频率中等。
- 使用平衡：净流量较小，起始次数和终点次数接近，表明这些站点的使用较为均衡。
- 中短途骑行：骑行时长适中，可能是一些中短途出行的主要站点。
建议：
- 保持资源配置：由于使用频率中等且均衡，建议保持这些站点的现有资源配置。
- 提高服务质量：持续优化这些站点的服务质量，提升用户满意度。

聚类 3

特征描述：
- 每天平均起始次数: 平均 21.30 次，标准差 9.97
- 每天平均终点次数: 平均 22.07 次，标准差 10.79
- 每天平均骑行次数差值（净流量）: 平均 -0.77 次，标准差 2.80
- 平均骑行时长: 平均 1394 秒，标准差 201 秒
情况划分：
- 使用频率较低：每天平均起始次数和终点次数较低，但高于聚类 0。
- 终点站使用更多：净流量为负，终点次数略高于起始次数，表明这些站点更常作为终点站使用。
- 长途骑行：骑行时长较长，可能是一些长途出行的主要站点。
建议：
- 增加自行车停放设施：由于终点站使用更多，建议增加这些站点的自行车停放设施，避免高峰期车辆积压。
- 优化调度：加强这些站点的车辆调度，确保在高峰期能够满足需求，尤其是将车辆调度到起始站。

聚类 4

特征描述：
- 每天平均起始次数: 平均 86.34 次，标准差 28.82
- 每天平均终点次数: 平均 114.35 次，标准差 25.62
- 每天平均骑行次数差值（净流量）: 平均 -28.01 次，标准差 10.80
- 平均骑行时长: 平均 1006 秒，标准差 132 秒
情况划分：
- 使用频率最高：每天平均起始次数和终点次数都非常高，表明这些站点使用频率极高。
- 终点站使用显著更多：净流量为负且数值较大，终点次数远高于起始次数，表明这些站点明显作为终点站使用。
- 高频站点：骑行时长较短，但使用频率高，可能是商业区、交通枢纽或重要办公区的站点。
建议：
- 大幅增加自行车停放设施：由于终点站使用显著更多，建议大幅增加这些站点的自行车停放设施，避免车辆积压问题。
- 强化调度和管理：这些站点使用频率极高，需要强化车辆调度和管理，确保高峰期有足够的车辆供应和停放空间。

6、方差分析

def anova_test(groups):
    anova_result = stats.f_oneway(*groups)
    return anova_result.statistic, anova_result.pvalue

results = []
hourly_groups = [data[data['hour'] == hour].groupby('Start date').size() for hour in range(24)]
stat, pval = anova_test(hourly_groups)
results.append(['Hour', stat, pval])

weekday_groups = [data[data['weekday'] == day].groupby('Start date').size() for day in data['weekday'].unique()]
stat, pval = anova_test(weekday_groups)
results.append(['Weekday', stat, pval])

station_groups = [data[data['Start station'] == station].groupby('Start date').size() for station in station_stats['Station']]
stat, pval = anova_test(station_groups)
results.append(['Station', stat, pval])

bike_model_groups = [data[data['Bike model'] == model].groupby('Start date').size() for model in data['Bike model'].unique()]
stat, pval = anova_test(bike_model_groups)
results.append(['Bike Model', stat, pval])

results_df = pd.DataFrame(results, columns=['特征', '统计值', 'p值'])

print(results_df)

在这里插入图片描述
总结：所有特征（骑行的开始时间、星期、站点、自行车型号）的p值均显著小于0.05，这表明这些特征对骑行次数均有显著影响，具体来说，不同时间段、不同星期几、不同站点以及不同自行车型号的骑行次数存在显著差异。因此，在进行运营优化时，应重点考虑这些特征对骑行需求的影响。

7、总结

本项目对伦敦共享单车数据进行了全面分析，涵盖了数据清洗、特征工程（构建新特征）、骑行高峰期分析、站点流量分析，以及通过聚类分析将800个站点划分为5类，并对每一类站点提出建议，最后通过方差分析探讨了影响共享单车流量的因素。得出的主要结论如下：

站点使用情况：
- 共有800个站点，最常用的起始站为Hyde Park Corner, Hyde Park，最常用的终点站为Waterloo Station 3, Waterloo。
每日骑行次数：
- 高峰日的骑行次数达到30132次（2023年8月9日），周三为骑行最高峰，总计136595次。
骑行时间分析：
- 最常见的骑行时间为7分48秒，共658次。
- 平均骑行时间为1097.73秒（约18.3分钟），标准差为1210.34秒，最短为60秒（1分钟），最长为28770秒（约8小时）。
自行车型号：
- 使用的自行车分为CLASSIC和ELECTRIC两种，其中CLASSIC的使用次数最多，共计677,259次。
骑行高峰时段：
- 每天的骑行高峰时段为下午3点至6点。
骑行时长波动：
- 大多数情况下，骑行的平均时长大致相同，但在某些日期骑行次数减少，总时长却增加，这表明这些日期的平均骑行时长有所不同。
- 8月的骑行总时长和次数显著波动，表明共享单车使用量随日期变化，与天气、节假日等因素有关。8月5日为显著低谷，与前后两天形成鲜明对比。
周骑行模式：
- 周二、周三、周四为骑行高峰期，无论骑行次数还是总时长都远高于其他时间；周六为低谷期，骑行次数和总时长都较短；周日骑行次数不多，但总时长较长，表明平均骑行时长高于周一和周五。
热门线路和站点：
- 热门线路多集中在公园和旅游景点附近，如Hyde Park Corner, Hyde Park为主要枢纽站点。
  Hyde Park、Waterloo和Liverpool Street周边为骑行活动集中地。运营者应在这些区域增加更多的自行车和停车设施，以满足高需求。
冷门站点分析：
- 冷门站点主要位于奥林匹克公园、汉默史密斯、帕特尼、坎纳里码头和拉德布鲁克格罗夫等区域。这些区域可能因地理位置或用途导致骑行需求较低。运营者可以考虑在这些低频使用站点减少资源配置，并通过推广活动提升使用率。
高低净流量站点：
- 高净流量站点需增加自行车供应，低净流量站点需增加停车设施，以接纳更多到达的自行车。
聚类分析结果：
- 聚类 0：使用频率较低，建议优化自行车资源配置，减少闲置车辆，并加强推广吸引用户。
- 聚类 1：终点站使用更多，建议增加自行车停放设施，避免高峰期积压，并加强车辆调度。
- 聚类 2：使用频率中等且均衡，建议保持现有资源配置，并持续优化服务质量。
- 聚类 3：终点站使用更多，建议增加自行车停放设施，避免高峰期积压，并加强车辆调度。
- 聚类 4：终点站使用显著更多，需大幅增加自行车停放设施，避免车辆积压，并强化车辆调度和管理。
影响因素分析：
- 不同时间段、星期几、站点和自行车型号的骑行次数存在显著差异。运营优化时，应重点考虑这些特征对骑行需求的影响。