4.2二叉树的基本概念二叉树的定义二叉树是n(n>=0)个节点的有限集合,1)n=0的时候,二叉树为空,2)n>=0的时候由根节点和两个互不相交的被称为根的左子树和右子树组成的,左子树和右子树也分别是一棵二叉树。五种基本的形态: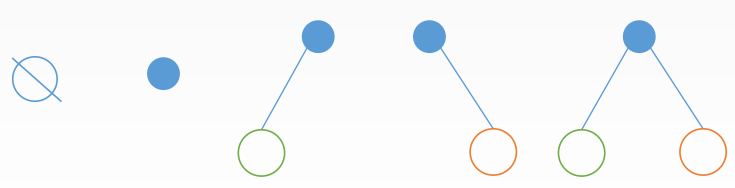 二叉树和度为2的有序树的比较1)二叉树可以为空,而度为2的有序树至少有三个结点2)二叉树的孩子结点始终有左右之分,而度为2的有序树的孩子结点次序是相对的。
二叉树和度为2的有序树的比较1)二叉树可以为空,而度为2的有序树至少有三个结点2)二叉树的孩子结点始终有左右之分,而度为2的有序树的孩子结点次序是相对的。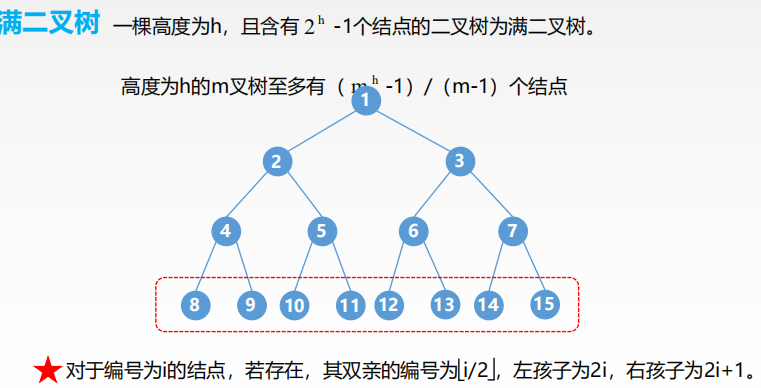
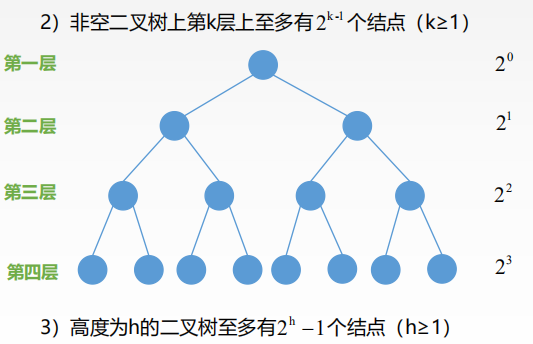
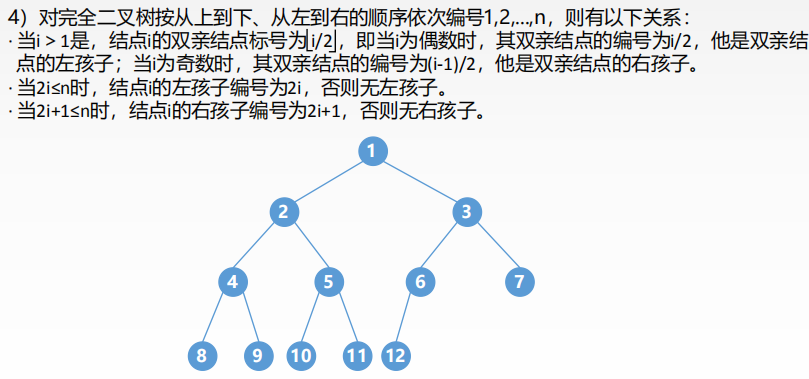
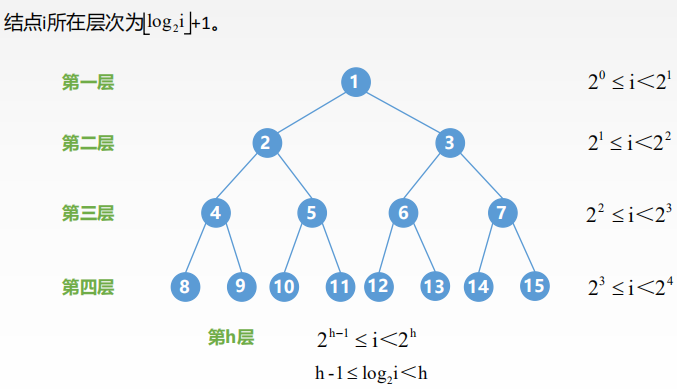
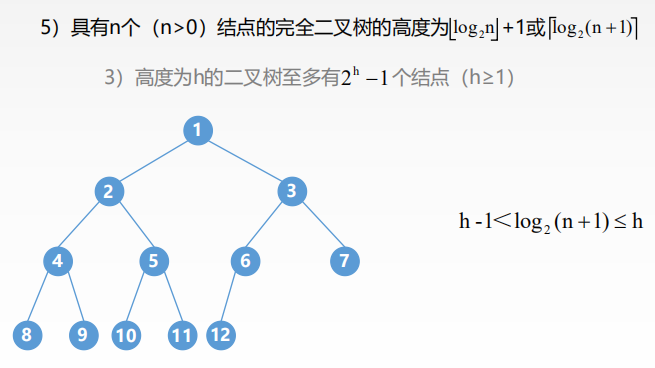
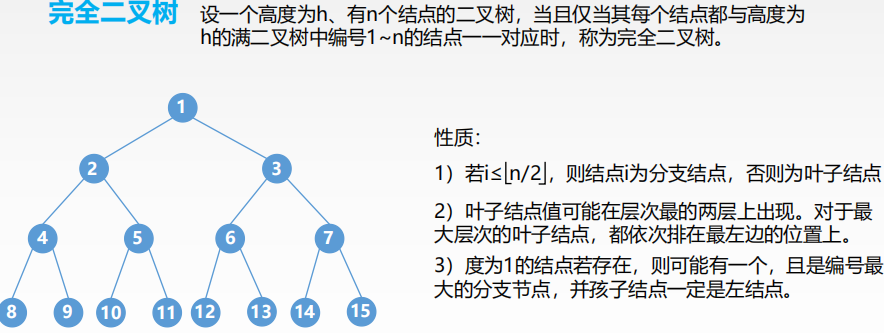 完全二叉树: 设一个高度为h,有n个节点的二叉树,当且仅当其每个结点都与高度为h的满二叉树单重编号1-n的结点一一对应,称为完全二叉树。二叉排序树:一棵二叉树,如果树非空则具有如下的性质: 对于任意的节点如果存在左子树或者右子树,则其左子树上的所有的节点的关键字都小于该结点,右子树上的所有的节点的关键字都大于该结点。平衡二叉树:树上任意节点的左子树和右子树的深度只差不超过1二叉树的性质:
完全二叉树: 设一个高度为h,有n个节点的二叉树,当且仅当其每个结点都与高度为h的满二叉树单重编号1-n的结点一一对应,称为完全二叉树。二叉排序树:一棵二叉树,如果树非空则具有如下的性质: 对于任意的节点如果存在左子树或者右子树,则其左子树上的所有的节点的关键字都小于该结点,右子树上的所有的节点的关键字都大于该结点。平衡二叉树:树上任意节点的左子树和右子树的深度只差不超过1二叉树的性质: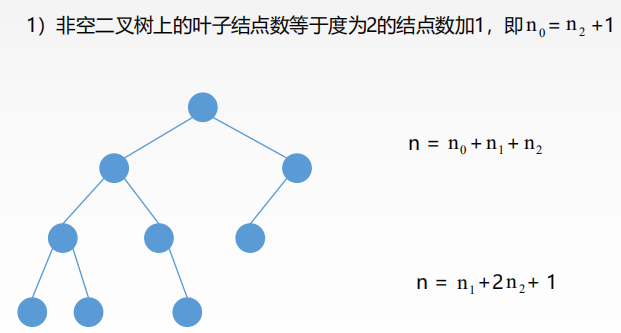


 ●R语言●句子●JAVA●C语言以及算法笔记●大学生生活图鉴●JavaScript●计算机网络原理●计算机组成原理●操作系统●数据库系统概论●数据结构●英语●Linux●读书电竞●云计算与人工智能●资源●明星电视剧社会现象娱乐
●R语言●句子●JAVA●C语言以及算法笔记●大学生生活图鉴●JavaScript●计算机网络原理●计算机组成原理●操作系统●数据库系统概论●数据结构●英语●Linux●读书电竞●云计算与人工智能●资源●明星电视剧社会现象娱乐


 仙女都在看点点点,赞和在看都在这儿!
仙女都在看点点点,赞和在看都在这儿!
 二叉树和度为2的有序树的比较1)二叉树可以为空,而度为2的有序树至少有三个结点2)二叉树的孩子结点始终有左右之分,而度为2的有序树的孩子结点次序是相对的。
二叉树和度为2的有序树的比较1)二叉树可以为空,而度为2的有序树至少有三个结点2)二叉树的孩子结点始终有左右之分,而度为2的有序树的孩子结点次序是相对的。
 完全二叉树: 设一个高度为h,有n个节点的二叉树,当且仅当其每个结点都与高度为h的满二叉树单重编号1-n的结点一一对应,称为完全二叉树。二叉排序树:一棵二叉树,如果树非空则具有如下的性质: 对于任意的节点如果存在左子树或者右子树,则其左子树上的所有的节点的关键字都小于该结点,右子树上的所有的节点的关键字都大于该结点。平衡二叉树:树上任意节点的左子树和右子树的深度只差不超过1二叉树的性质:
完全二叉树: 设一个高度为h,有n个节点的二叉树,当且仅当其每个结点都与高度为h的满二叉树单重编号1-n的结点一一对应,称为完全二叉树。二叉排序树:一棵二叉树,如果树非空则具有如下的性质: 对于任意的节点如果存在左子树或者右子树,则其左子树上的所有的节点的关键字都小于该结点,右子树上的所有的节点的关键字都大于该结点。平衡二叉树:树上任意节点的左子树和右子树的深度只差不超过1二叉树的性质:





欢迎打赏,么么哒!

 ●R语言●句子●JAVA●C语言以及算法笔记●大学生生活图鉴●JavaScript●计算机网络原理●计算机组成原理●操作系统●数据库系统概论●数据结构●英语●Linux●读书电竞●云计算与人工智能●资源●明星电视剧社会现象娱乐
●R语言●句子●JAVA●C语言以及算法笔记●大学生生活图鉴●JavaScript●计算机网络原理●计算机组成原理●操作系统●数据库系统概论●数据结构●英语●Linux●读书电竞●云计算与人工智能●资源●明星电视剧社会现象娱乐


 仙女都在看点点点,赞和在看都在这儿!
仙女都在看点点点,赞和在看都在这儿!




 本文介绍了二叉树的基本概念,包括空树、完全二叉树和二叉排序树的定义。完全二叉树是一种特定形态的二叉树,而二叉排序树则保证了节点的左子树所有关键字小于父节点,右子树所有关键字大于父节点。此外,还提到了平衡二叉树的概念,这种树的左右子树深度差不超过1,确保了高效查找性能。
本文介绍了二叉树的基本概念,包括空树、完全二叉树和二叉排序树的定义。完全二叉树是一种特定形态的二叉树,而二叉排序树则保证了节点的左子树所有关键字小于父节点,右子树所有关键字大于父节点。此外,还提到了平衡二叉树的概念,这种树的左右子树深度差不超过1,确保了高效查找性能。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








