二阶系统阶跃响应实验_如何理解单自由度系统振动

一、数学模型
二、自由振动
    2.1无阻尼自由度振动
    2.2有阻尼自由度振动
三、受迫振动
    3.1 无阻尼受迫振动（正弦激励）
    3.2 有阻尼受迫振动（正弦激励）
    3.3 有阻尼受迫振动（阶跃激励）
    3.4 有阻尼受迫振动（冲击响应）

---

一、数学模型

对于很多工程而言，动态特性是非常重要的考核指标，其本质就是两个变量及其关系：力和位移。对于对象可以简化成质点或者刚体的问题，这个问题其实伟大的牛爵爷已经解决了，即牛顿第二定律：

对应的力我们称之为惯性力，实际工程上和位移相关的不仅仅有

惯性力，还有其它的力，比如和速度相关的（位移的导数） 阻尼力，以及和位移线性相关的 弹性力，同时包含惯性力、阻尼力和弹性力的模型就是我们常说的 单自由度弹簧振子系统，具体数学模型如下：

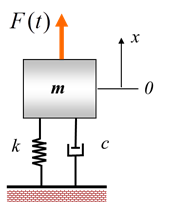
则根据力平衡方程，可以得到：

其中：

——质量块质量；

——阻尼系数；

——弹簧刚度；

——质量块位移；

——外界施加力。

对上式两端进行拉普拉斯变换，可以的到：

即系统的传递函数为：

从数学上看，这是一个典型的二阶系统，我们知道，绝大多数工程中系统都可以降阶为一阶系统和二阶系统的叠加，一阶系统非常简单，通过常我们关注的和难解决的都是二阶分量对应的模态，因此理解如上单自由度弹簧振子模型（二阶系统）的响应特性非常重要。

从物理上看，对于单自由度系统而言，都可以简化为如上模型；当系统是更复杂的连续系统时，一般更关心一阶模态的振动（动态特性），这也可简化成单自由度振动，因此理解单自由度系统振动是理解其他一切振动的基础。

比如，对于飞机的飞行控制，其实就是将飞机的纵向运动降阶为两个二阶运动（长周期运动和短周期运动），进而加以控制，具体见下文：

https://zhuanlan.zhihu.com/p/91047110

单自由度系统的振动可以分成两大部分：自由振动（无外力

）和 受迫振动（有外力

）。

---

二、自由振动

当

时，称弹簧振子系统为自由振动，根据系统中阻尼的情况，自由振动又可分为

无阻尼自由振动和 有阻尼自由振动。为简单起见，先分析无阻尼自由振动。

2.1无阻尼自由振动

当系统为无阻尼自由振动时，对弹簧振子而言，其机械能是守恒的，振动的本质就是动能和势能之间的互相转换，系统做等幅振动。

此时，阻尼系数

，带入振动方程有：

设

则振动方程可以改写为：

这是一个典型的二阶微分方程，其通解形式为：

或者写成更紧凑的形式：

设系统的初始条件为：

时，有

，

，则带入微分方程的通解可以得到：

即方程的解为：

当通解写成指数形式时，可以得到：

二阶线性振动微分方程的解释时间

的简谐函数，方程解中的

只决定于系统本身的参数

和

，而与系统的初始条件无关，是系统本身的固有特性，称之为

固有频率。方程解中的

称为振幅，是质量块偏离静平衡位置的最大距离，

称为初相位。

搭建仿真模型如下：

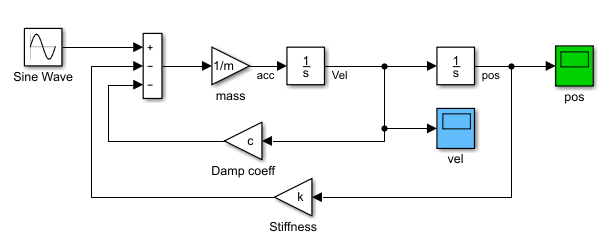
xi=0;%阻尼比为0
wn=1;%固有频率为1rad/s； 

m=1;%质量为1Kg；
k=m*wn^2;%刚度，N/m；
c=2*sqrt(m*k)*xi; %阻尼系数，N/(m/s)
F0=0; %正弦激励振幅，m；
w=0.5;%正弦激励频率，rad/s； 

v0=1; %初始速度，m/s；
x0=2; %初始位移，m；

仿真波形如下：

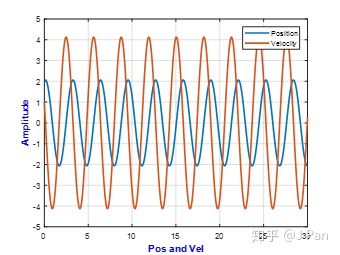
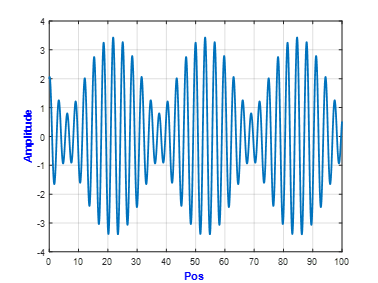
可见，对于无阻尼自由振动，当有初始速度/位移时，系统做等幅振动。

2