本文详细介绍如何使用TensorFlow进行线性回归、非线性回归及逻辑回归，包括代码实现、模型训练与评估。通过实例，读者可以学习如何在TensorFlow环境中构建回归模型，理解损失函数、优化器的作用，以及如何调整模型参数以获得最佳拟合。
2.1 基于TensorFlow线性回归
本实验将学习如果在TensorFlow环境下进行线性回归。
方框中的代码您可以复制到远程桌面的jupyter notebook中，建议手动输入以达到更高的学习效果。
开始我们的实验！
键入如下代码加载相关的包：
import numpy as np
import tensorflow as tf
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (10, 6)
键入如下代码生成随机数点：接下来，我们通过生成随机数来定义一个线性关系。
x_data = np.random.rand(100).astype(np.float32)
键入如下代码定义线性关系：
y_data = x_data * 3 + 2
y_data = np.vectorize(lambda y: y + np.random.normal(loc=0.0, scale=0.1))(y_data)
解释：我们定义了 Y=3X+2 的线性关系。为了模仿实际数据，我们在Y值上加入了高斯噪声。
接下来，我们通过TensorFlow来线性拟合以上的数据。
键入如下代码，设置TensorFlow变量：
a = tf.Variable(1.0)
b = tf.Variable(0.2)
y = a * x_data + b
解释：a、b分别代表线性拟合Y=AX+B中的的A和B。其后的1.0和0.2位初始值，您可以更改为任意值，通过以下的拟合，将会找到适合模拟数据的a、d的值，就是上面定义的3和2（但是会有一些误差，因为加入了随机数）。
键入如下代码，定义损失函数：
loss = tf.reduce_mean(tf.square(y - y_data))
解释：使用均方误差作为损失值。
键入如下代码，选择训练的优化器，并定义学习率：
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
解释：通过优化器，是的损失函数一步一步减小，最后得到拟合效果。
键入如下代码，初始化变量：
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
解释：TensorFlow是基于数据流图(data flow graphs)技术来进行数值计算，在每个计算开始时，我们需要打开一个会话，会话是在TensorFlow中创建图形的上下文，会话开始时，需要初始化变量。
键入如下代码，开始训练我们的模型：
train_data = []
for step in range(100):
evals = sess.run([train,a,b])[1:]
if step % 5 == 0:
print(step, evals)
train_data.append(evals)
结果：
0 [2.5903053, 3.005062]
10 [2.655332, 2.1889384]
20 [2.8404162, 2.0889323]
30 [2.9278822, 2.0416725]
40 [2.969216, 2.019339]
50 [2.9887495, 2.0087848]
60 [2.9979804, 2.003797]
70 [3.0023425, 2.0014403]
80 [3.004404, 2.0003262]
90 [3.0053782, 1.9998]
解释：结果输出了在每10次迭代后，a、b的拟合值。可以发现，它们慢慢的接近我们最开始定义的值
键入如下代码，绘制拟合过程图：
converter = plt.colors
for f in train_data:
[a, b] = f
f_y = np.vectorize(lambda x: a*x + b)(x_data)
line = plt.plot(x_data, f_y)
plt.setp(line, color=(1,1,0))
plt.plot(x_data, y_data, 'ro')
fy = x_data*evals[0]+evals[1]
line = plt.plot(x_data, f_y)
plt.setp(line, color=(0,0,1))
f_line = mpatches.Patch(color='red', label='Data Points')
plt.legend(handles=[f_line])
plt.show()
print(evals)
结果：
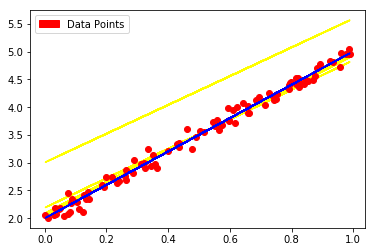
[3.0058064, 1.9995685]
解释：蓝色线为最终拟合的线，a、b的拟合值分别为3.005806和1.9995685.
2.2 基于TensorFlow非线性回归
本实验将学习如果使用TensorFlow进行非线性回归
首先键入如下代码，加载相应的包：
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
键入如下代码，构建模拟数据，并展示：
np.random.seed(1)
x_data = np.arange(-2.0, 3.0, 0.05)
beta0=2
beta1=-1
beta2=-2 # 这表示二次项
beta3=1 # 这表示三次项
y_data = beta0 + beta1*x_data + beta2*(x_data**2)+ beta3*(x_data**3)\
+ np.random.normal(0,3,len(x_data))
plt.plot(x_data,y_data,'o')
plt.ylabel('Dependent Variable')
plt.xlabel('Indepdendent Variable')
plt.show()
结果：
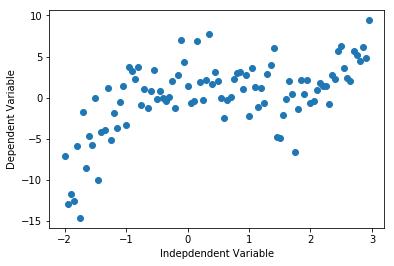
解释：同样地，模拟数据由非线性函数加噪声得到。
于是我们得到了一串观测值 [x_data , y_data]，接下来我们通过非线性拟合得到它们的关系表达式。观察上图可以看出图形走势有两个拐弯处，所以我们可以初步决定由3次多项式拟合。
键入如下代码，在TensorFlow中建立占位符、变量和表达式：
#输入模型，即'X'变量
#注意，占位符意味着当我们调用tensorflow范式时我们已经传递了这个参数
x = tf.placeholder(tf.float32, shape=(x_data.size))
y = tf.placeholder(tf.float32,shape=(y_data.size))
# tf.Variable调用在内存中创建一个可更新的副本并高效地更新
# 该副本通过tensorflow会话的范围来重新传输变量值中的任何更改
beta_0 = tf.Variable(2.0)
beta_1 = tf.Variable(3.0)
beta_2 = tf.Variable(4.0)
beta_3 = tf.Variable(5.0)
y_pred = tf.add( beta_0,
tf.add( tf.multiply(beta_1,x),
tf.add( tf.multiply(beta_2, tf.multiply(x,x)),
tf.multiply(beta_3, tf.multiply(x,tf.multiply(x,x))))))
解释：其中beta_0到beta_3为拟合参数的初始值，您可以随意更改。
键入如下代码，初始化会话，并显示初始拟合函数：
#创建session，并初始化变量
session = tf.Session()
session.run(tf.global_variables_initializer())
#用初始参数值进行预测
pred = session.run(y_pred, feed_dict={x:x_data, y:y_data})
#根据数据点绘制初始预测
plt.plot(x_data, pred)
plt.plot(x_data, y_data, 'ro')
结果:
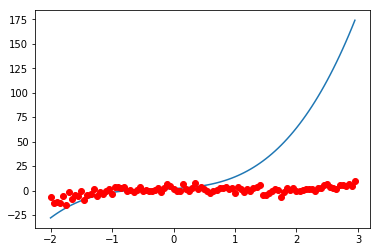
解释：此处蓝色为我们初始化设置的拟合的曲线，可以看出与样本差别很大，通过下面的拟合方法，将会得到较好的拟合效果。
键入如下代码，设置损失函数：
# 标准化因子
nf = 1e-1
# 设置损失函数
loss = tf.reduce_mean(tf.squared_difference(y_pred*nf,y*nf))
键入如下代码，设置优化器：
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
# 通过优化器应优化的损失函数
train = optimizer.minimize(loss)
session.run(tf.global_variables_initializer())
键入如下代码，开始训练，并输出每1000次迭代后的损失值：
losses = [float("Inf")]
epoch = 10000 #1000000
#循环训练
for steps in range(epoch):
t,l = session.run([train, loss], feed_dict={x:x_data,y:y_data})
losses.append(l)
#如果损失开始改变小于1e-7，则停止训练
if abs(losses[-1] - losses[-2]) < 10^-3:
break
if steps%1000 == 0:
print("steps = %d loss = %f"%(steps,losses[steps]))
print("steps = %d loss = %f"%(steps,losses[steps]))
结果：
steps = 0 loss = inf
steps = 1000 loss = 0.197009
steps = 2000 loss = 0.119587
steps = 3000 loss = 0.100819
steps = 4000 loss = 0.094441
steps = 5000 loss = 0.090922
steps = 6000 loss = 0.088264
steps = 7000 loss = 0.086021
steps = 8000 loss = 0.084070
steps = 9000 loss = 0.082359
steps = 9999 loss = 0.080854
键入如下代码，输出拟合参数，并查看拟合效果：
#从训练模型中得出预测值
pred,b0, b1, b2, b3 = session.run([y_pred, beta_0, beta_1, beta_2, beta_3], feed_dict={x:x_data,y:y_data})
#根据数据点绘制预测图
plt.plot(x_data, pred)
plt.plot(x_data, y_data, 'ro')
#输出最终参数
print("beta_0 = %f, beta_1 = %f, beta_2 = %f, beta_3 = %f" % (b0,b1, b2, b3))
结果：beta_0 = 1.004781, beta_1 = 1.094178, beta_2 = -1.357563, beta_3 = 0.501319
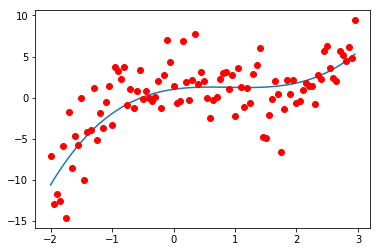
键入如下代码，查看训练过程中损失值变化情况：
plt.plot(losses)
结果：
2.3 基于TensorFlow逻辑回归
本实验将学习如果使用TensorFlow进行逻辑回归来实现分类。
本实验采用Iris数据集：Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。数据集包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性。可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。
开始我们的实验！
键入如下代码，加载本实验相关的包：
import tensorflow as tf
import pandas as pd
import numpy as np
import time
from sklearn.datasets import load_iris
from sklearn.cross_validation import train_test_split
import matplotlib.pyplot as plt
键入如下代码，设置我们的数据，并查看数据集大小：
iris = load_iris()
iris_X, iris_y = iris.data[:-1,:], iris.target[:-1]
iris_y= pd.get_dummies(iris_y).values
trainX, testX, trainY, testY = train_test_split(iris_X, iris_y, test_size=0.33, random_state=42)
print(trainX.shape)
print(testX.shape)
print(trainY.shape)
print(testY.shape)
结果：
(99, 4)
(50, 4)
(99, 3)
(50, 3)
解释：通过train_test_split函数中的设置，将数据集按1:3的比例分割了数据，分别作为训练集和测试集。
键入如下代码，设置占位符和变量：
# numFeatures是我们输入数据中的特征数量。
# 在iris数据集中，这个数字是'4'
numFeatures = trainX.shape[1]
# numLabels使我们数据集的类的数量
# 在iris数据集中，这个数字是'3'
numLabels = trainY.shape[1]
# 占位符
# 'None' 意味着TensorFlow不应该期望在该维度中有一个固定的数字
X = tf.placeholder(tf.float32, [None, numFeatures]) # Iris 有4个特征，所以X是来保存我们的数据的张量
yGold = tf.placeholder(tf.float32, [None, numLabels]) # 这将是我们的3个类矩阵的正确答案
W = tf.Variable(tf.zeros([4, 3])) # 4维输入和3个类
b = tf.Variable(tf.zeros([3])) # 3维输出 [0,0,1],[0,1,0],[1,0,0]
#随机抽取标准偏差为.01的正态分布
weights = tf.Variable(tf.random_normal([numFeatures,numLabels],
mean=0,
stddev=0.01,
name="weights"))
bias = tf.Variable(tf.random_normal([1,numLabels],
mean=0,
stddev=0.01,
name="bias"))
键入如下代码，定义Logistic回归：
# Logistic回归方程的三要素分解
# 注意这些feed到其他
apply_weights_OP = tf.matmul(X, weights, name="apply_weights")
add_bias_OP = tf.add(apply_weights_OP, bias, name="add_bias")
activation_OP = tf.nn.sigmoid(add_bias_OP, name="activation")
键入如下代码，设置迭代次数和学习率：
# 我们训练中的Epochs数
numEpochs = 700
# 定义我们的学习率迭代 (衰减)
learningRate = tf.train.exponential_decay(learning_rate=0.0008,
global_step= 1,
decay_steps=trainX.shape[0],
decay_rate= 0.95,
staircase=True)
键入如下代码，设置损失函数：
#定义我们的成本函数 - 平方均值误差
cost_OP = tf.nn.l2_loss(activation_OP-yGold, name="squared_error_cost")
#定义我们的渐变下降
training_OP = tf.train.GradientDescentOptimizer(learningRate).minimize(cost_OP)
键入如下代码，初始化会话：
# 创建一个tensorflow会话
sess = tf.Session()
# 初始化我们的权重和偏差变量
init_OP = tf.global_variables_initializer()
# 初始化所有tensorflow变量
sess.run(init_OP)
键入如下代码，设置一些变量追踪我们的训练：
# argmax(activation_OP, 1)以最大概率返回标签
# argmax(yGold, 1)是正确的标签
correct_predictions_OP = tf.equal(tf.argmax(activation_OP,1),tf.argmax(yGold,1))
# 如果每个错误预测为0并且每个真实预测为1，则平均值会返回我们的准确性
accuracy_OP = tf.reduce_mean(tf.cast(correct_predictions_OP, "float"))
# 汇总op的回归输出
activation_summary_OP = tf.summary.histogram("output", activation_OP)
# 汇总op的准确度
accuracy_summary_OP = tf.summary.scalar("accuracy", accuracy_OP)
# 汇总op的成本
cost_summary_OP = tf.summary.scalar("cost", cost_OP)
# 汇总检查每次迭代后变量(W, b) 是如何更新
weightSummary = tf.summary.histogram("weights", weights.eval(session=sess))
biasSummary = tf.summary.histogram("biases", bias.eval(session=sess))
# 合并所有的汇总
merged = tf.summary.merge([activation_summary_OP, accuracy_summary_OP, cost_summary_OP, weightSummary, biasSummary])
# 汇总writer
writer = tf.summary.FileWriter("summary_logs", sess.graph)
键入如下代码，开始训练，并输出训练过程：
# 初始化报告变量
cost = 0
diff = 1
epoch_values = []
accuracy_values = []
cost_values = []
# 训练 epochs
for i in range(numEpochs):
if i > 1 and diff < .0001:
print("change in cost %g; convergence."%diff)
break
else:
# 运行训练
step = sess.run(training_OP, feed_dict={X: trainX, yGold: trainY})
# Report occasional stats
if i % 100 == 0:
# 将epoch添加到epoch_values
epoch_values.append(i)
# 基于测试集数据生成准确度
train_accuracy, newCost = sess.run([accuracy_OP, cost_OP], feed_dict={X: trainX, yGold: trainY})
# 为实时图形变量添加准确性
accuracy_values.append(train_accuracy)
# 为实时图形变量添加成本
cost_values.append(newCost)
# 对变量重新分配值
diff = abs(newCost - cost)
cost = newCost
#生成输出语句
print("step %d, training accuracy %g, cost %g, change in cost %g"%(i, train_accuracy, newCost, diff))
# How well do we perform on held-out test data?
print("final accuracy on test set: %s" %str(sess.run(accuracy_OP,
feed_dict={X: testX,
yGold: testY})))
结果：
step 0, training accuracy 0.333333, cost 34.0801, change in cost 34.0801
step 100, training accuracy 0.666667, cost 20.6582, change in cost 13.4219
step 200, training accuracy 0.717172, cost 18.0602, change in cost 2.59801
step 300, training accuracy 0.787879, cost 16.9067, change in cost 1.15349
step 400, training accuracy 0.848485, cost 16.1811, change in cost 0.725594
step 500, training accuracy 0.878788, cost 15.6475, change in cost 0.533636
step 600, training accuracy 0.909091, cost 15.2231, change in cost 0.424445
final accuracy on test set: 0.9
解释：每迭代100次输出训练结果，可以看出最后的预测准确率accuracy 达到了90％.
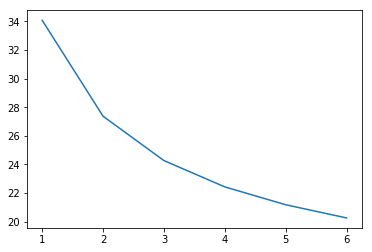
键入如下代码，查看训练过程损失值变化情况：
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.plot([np.mean(cost_values[i-50:i]) for i in range(len(cost_values))])
plt.show()
结果：
3.1 知识点补充
在网络训练中用到优化器和激励函数，事实上存在多种优化器和激励函数，如下：
更多优化器：
tf.train.GradientDescentOptimizer
tf.train.AdadeltaOptimizer
tf.train.AdagradOptimizer
tf.train.MomentumOptimizer
tf.train.AdamOptimizer
更多激励函数:Activation Functioins
tf.nn.relu
tf.nn.relu6
tf.nn.elu
tf.nn.softplus
tf.nn.softsign
tf.nn.dropout
tf.nn.bias_add
tf.sigmoid
tf.tanh
您可以尝试更换优化器和激励函数，对比效果。
3.2 作业
请以下面数据，完成拟合任务吧。
拟合数据是有关年龄、体重与血液脂肪含量的多元线性关系数据。
数据每列代表：
Index One Weight (kilograms) Age (Years) Blood fat content
1 1 84 46 354
2 1 73 20 190
3 1 65 52 405
4 1 70 30 263
5 1 76 57 451
6 1 69 25 302
7 1 63 28 288
8 1 72 36 385
9 1 79 57 402
10 1 75 44 365
11 1 27 24 209
12 1 89 31 290
13 1 65 52 346
14 1 57 23 254
15 1 59 60 395
16 1 69 48 434
17 1 60 34 220
18 1 79 51 374
19 1 75 50 308
20 1 82 34 220
21 1 59 46 311
22 1 67 23 181
23 1 85 37 274
24 1 55 40 303
25 1 63 30 244
在以下“请输入代码处”完成完整的拟合代码：
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
# 此处请输入自己的拟合数据，可以模拟构造，也可以使用真实数据
# 请输入代码
plt.plot(x_data,y_data,'o')
plt.ylabel('Dependent Variable')
plt.xlabel('Indepdendent Variable')
plt.show()
# 通过观察拟合数据，选择合适的非线性函数
# 请输入代码
session = tf.Session()
session.run(tf.global_variables_initializer())
pred = session.run(y_pred, feed_dict={x:x_data, y:y_data})
plt.plot(x_data, pred)
plt.plot(x_data, y_data, 'ro')
nf = 1e-1
loss = tf.reduce_mean(tf.squared_difference(y_pred*nf,y*nf))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
train = optimizer.minimize(loss)
session.run(tf.global_variables_initializer())
losses = [float("Inf")]
epoch = 10000
for steps in range(epoch):
t,l = session.run([train, loss], feed_dict={x:x_data,y:y_data})
losses.append(l)
if abs(losses[-1] - losses[-2]) < 10^-3:
break
if steps%1000 == 0:
print("steps = %d loss = %f"%(steps,losses[steps]))
print("steps = %d loss = %f"%(steps,losses[steps]))
# 输入预测值
# 请输入代码：
扫一扫
1115
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
