14.1 数据结构的介绍
作为(单)链表的升级版,我们通常接触的树都是二叉树(binary tree),即每个节点最多有两个子节点;树与链表的主要差别就是多了一个子节点的指针。
14.2 树的递归
树递归的写法与深度优先搜索的递归写法相同
题目代号: 104 二叉树的最大深度
题目描述:
求一个二叉树的最大深度。
测试用例:

output:3
我的分析:
看左递归和右递归的最大值+1即可
代码:
public int maxDepth(TreeNode root) {
if(root == null){
return 0;
}else {
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
return Math.max(leftDepth,rightDepth)+1;
}
题目代号: 110 平衡二叉树
题目描述:
判断一个二叉树是否平衡。树平衡的定义是,对于树上的任意节点,其两侧节点的最大深度的差值不得大于 1。
测试用例:

我的分析:
解法类似于求树的最大深度,但有两个不同的地方:
一是我们需要先处理子树的深度再进行比较,
二是如果我们在处理子树时发现其已经不平衡了,则可以返回一个-1,使得所有其长辈节点可以避免多余的判断
代码:
public boolean isBalanced(TreeNode root) {
if(height(root) == -1){
return false;
}else {
return true;
}
}
public int height(TreeNode root){
if (root == null) {
return 0;
}
int left = height(root.left);
int right = height(root.right);
if(left == -1 || right == -1 || Math.abs(left - right) > 1){
return -1;
}else {
return Math.max(left,right)+1;
}
}
题目代号: 543 二叉树的直径
题目描述:
求一个二叉树的最长直径。直径的定义是二叉树上任意两节点之间的无向距离。
测试用例:

我的分析:
在我们处理某个子树时,我们更新的
最长直径值和递归返回的值是不同的。这是因为待更新的最长直径值是(两侧长度);而函数返回值是(一侧长度),
代码:
int ans = 0;
public int diameterOfBinaryTree(TreeNode root) {
depth(root);//这样已经知道了maxd了
return ans;
}
public int depth(TreeNode node){
if(node==null){
return 0;
}
int Left = depth(node.left);// 左儿子为根的子树的深度
int Right = depth(node.right);// 右儿子为根的子树的深度
ans=Math.max(Left+Right,ans);//将每个节点最大直径(左子树深度+右子树深度)当前最大值比较并取大者
//如果隐去上一行就是求最长长度,不管左右,所以上一行就把左右加起来了
return Math.max(Left,Right)+1;//返回节点深度
}
题目代号: 437 路径总和III
题目描述:
给定一个整数二叉树,求有多少条路径节点值的和等于给定值。
测试用例:

我的分析:
一个节点一个节点的来判断,先对于根节点来说,如果能找到的话,就count = 1;
然后它的左儿子递归,右儿子递归,所有的加起来就可以了
代码:
public int pathSum(TreeNode root, int targetSum) {
if(root == null){
return 0;
}else {
return helper(root,targetSum) + pathSum(root.left,targetSum) + pathSum(root.right,targetSum);
}
}
public int helper(TreeNode root,int targetSum){//专门用来计算连续加入节点的路径
if(root == null) return 0;
int count = 0;
if(root.val == targetSum){
count = 1;
}else {
count = 0;
}
count += helper(root.left,targetSum - root.val);
count += helper(root.right,targetSum - root.val);
return count;//只要有符合的路径,返回值一定是1
}
题目代号: 101 对称二叉树
题目描述:
判断一个二叉树是否对称。
测试用例:

我的分析:
笔者一般习惯将判断两个子树是否相等或对称类型的题的解法叫做“四步法”:
(1)如果两个子树都为空指针,则它们相等或对称
(2)如果两个子树只有一个为空指针,则它们不相等或不对称
(3)如果两个子树根节点的值不相等,则它们不相等或不对称
(4)根据相等或对称要求,进行递归处理。
代码:
public boolean isSymmetric(TreeNode root) {
if(root == null){
return true;
}else {
return check(root.left,root.right);
}
}
public boolean check(TreeNode l,TreeNode r){//这是两个指针,一个向左移动,另一个向右移动,若向右移动的等于向左移动的 或者向左移动的等于向右移动的 那就可以了
if(l == null && r == null){
return true;
}else if(l == null || r == null) {
return false;
}else if(l.val != r.val){
return false;
}else {
return check(l.left,r.right) && check(l.right,r.left);
}
}
14.3 层次遍历
题目代号: 637 二叉树的层平均值
题目描述:
给定一个二叉树,求每一层的节点值的平均数
测试用例:

我的分析:
肯定是广度优先遍历了,就创建一个队列,先把头节点加入队列
对于任意一层来说,我们先遍历队列,来知道这个队列的长度,和;遍历这个队列,计算他们的加和,弹出当前层,当前层加和,下一层顺带着加入队列
for循环一次,就一层结束,几层就for几次
代码:
public List<Double> averageOfLevels(TreeNode root) {
List<Double> averages = new ArrayList<Double>();
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
double sum = 0;
int size = queue.size();
for (int i = 0; i < size; i++) {//遍历这个队列,弹出当前层,当前层加和,引入下一层
TreeNode node = queue.poll();
sum += node.val;
TreeNode left = node.left, right = node.right;
if (left != null) {
queue.offer(left);
}
if (right != null) {
queue.offer(right);
}
}//出了这一层,就代表这一层的和求出来了
averages.add(sum / size);
}
return averages;
}
14.4 前中后序遍历
题目代号: 105 从前序与中序遍历序列构造二叉树
题目描述:
给定一个二叉树的前序遍历和中序遍历结果,尝试复原这个树
测试用例:

我的分析:
- 1、根据根节点在前序遍历中头一个的位置去找根节点在中序遍历中的位置
2、根据根节点在中序遍历中的位置划分开左半子树和右半子树(用一个HashMap把中序遍历数组的每个元素的值和下标存起来,为了方便寻找寻找根节点的位置。)
3、我们就知道了左半子树和右半子树的长度,从前序遍历中就划分开了
4、左半子树和右半子树在前序遍历和中序遍历中都区分开了
代码:
public TreeNode buildTree(int[] preorder, int[] inorder) {
//把中序遍历的元素放入hashmap中
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return buildTreeHelper(preorder, 0, preorder.length, inorder, 0, inorder.length, map);
}
private TreeNode buildTreeHelper(int[] preorder, int pre_start, int pre_end, int[] inorder, int in_start, int in_end,
HashMap<Integer, Integer> map) {
if (pre_start == pre_end) {
return null;
}
int root_val = preorder[pre_start];//1、根节点就是前序遍历的头一个(这个观点在子部分也成立)
TreeNode root = new TreeNode(root_val);//把这个节点添加到构建的树上
int i_root_index = map.get(root_val);//2、获得这个根节点在中序遍历中的下标
int leftNum = i_root_index - in_start;//左子树的长度
//递归的构造左子树
root.left = buildTreeHelper(preorder, pre_start + 1, pre_start + leftNum + 1, inorder, in_start, i_root_index, map);
//起始位置就是这个位置,结束位置多+1
//递归的构造右子树
root.right = buildTreeHelper(preorder, pre_start + leftNum + 1, pre_end, inorder, i_root_index + 1, in_end, map);
return root;
}
题目代号: 144. 二叉树的前序遍历
题目描述:
给你二叉树的根节点 root ,返回它节点值的 前序 遍历
测试用例:

我的分析:
递归 == 栈 == 深度优先遍历
代码:
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<Integer>();//先构造个数组来存放之后的前序遍历
helper(root,list);
return list;
}
public void helper(TreeNode root,List<Integer> list){
if(root==null){
return;
}
list.add(root.val);
helper(root.left,list);
helper(root.right,list);
}
// 先右后左,保证左子树先遍历
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) {
return res;
}
Deque<TreeNode> stack = new LinkedList<>();
stack.push(root);//把头节点压入栈
while (!stack.isEmpty()) {
TreeNode temp = stack.poll();//把栈中节点弹出来,添加到树上
res.add(temp.val);//把节点值加入到列表中
if (temp.right != null) {//只要这棵树的儿子节点不是空,就加入到栈中
stack.push(temp.right);
}
if (temp.left != null) {
stack.push(temp.left);
}
}
return res;
}
14.5 二叉查找树
二叉查找树(BinarySearchTree,BST)是一种特殊的二叉树:对于每个父节点,其左子节点的值小于等于父结点的值,其右子节点的值大于等于父结点的值。
因此对于一个二叉查找树,我们可以在O(nlogn)的时间内查找一个值是否存在:从根节点开始,若当前节点的值大于查找值则向左下走,若当前节点的值小于查找值则向右下走。同时因为二叉查找树是有序的,对其中序遍历的结果即为排好序的数组。
题目代号: 99 恢复二叉搜索树
题目描述:
给定一个二叉查找树,已知有两个节点被不小心交换了,试复原此树
测试用例:
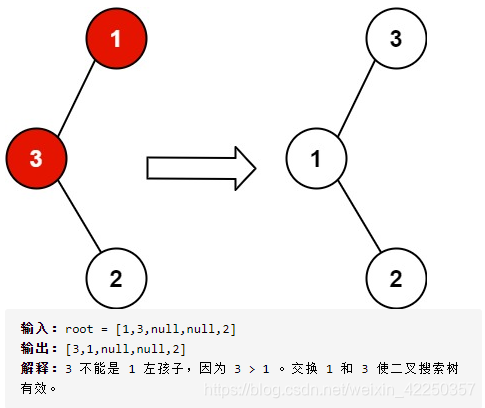
我的分析:
1、先把二叉寻找树遍历下,中序遍历放进list数组中
2、从list列表中找到有问题的两个数
此处你要注意:这俩数可能挨着,也可能不挨着
3、把树中的两个节点交换就好了
代码:
public void recoverTree(TreeNode root) {
/*
1、先把二叉寻找树遍历下,中序遍历放进list数组中
2、从list列表中找到有问题的两个数
此处你要注意:这俩数可能挨着,也可能不挨着
3、把树中的两个节点交换就好了
*/
List<TreeNode> list = new ArrayList<TreeNode>();
dfs(root,list);//放进list里面了
TreeNode x = null;
TreeNode y = null;
//扫面遍历的结果,找出可能存在错误交换的节点x和y
for(int i = 0;i < list.size()-1;i++){
if(list.get(i).val > list.get(i+1).val){
y = list.get(i+1);//这个后面值可能之后还要换,就看有问题的值是不是挨着了
if(x == null){
x = list.get(i);//你想一下哈,这个前面的值只能换一次
}
}
}
//如果x和y不为空,则交换这两个节点值,恢复二叉搜索树
if(x != null && y != null){
int temp = x.val;
x.val = y.val;
y.val = temp;
}
}
//中序遍历二叉树,并将遍历的结果保存到list中
public void dfs(TreeNode node,List<TreeNode> list){
if(node == null){
return;
}
dfs(node.left,list);
list.add(node);
dfs(node.right,list);
}
题目代号: 669 修剪二叉搜索树
题目描述:
给定一个二叉查找树和两个整数 L 和 R,且 L < R,试修剪此二叉查找树,使得修剪后所有
节点的值都在 [L, R] 的范围内
测试用例:

我的分析:
我们就进行递归就好了,从根节点、左半子树、右半子树进行考虑
跟节点大于最大值,那么右半子树全砍掉
根节点小于最小值,那么左半子树全砍掉
左半子树 = 对左半子树进行递归
右半子树 = 对右半子树进行递归
代码:
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root == null){
return root;
}
if(root.val > high){//如果根节点大于最高点,那说明右半子树需要全被砍掉
return trimBST(root.left,low,high);
}
if(root.val < low){//如果根节点小于最高点,那说明左半子树需要全被砍掉
return trimBST(root.right,low,high);
}
root.left = trimBST(root.left,low,high);//左半子树进行递归
root.right = trimBST(root.right,low,high);//右半子树进行递归
return root;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








