剑指offer—栈和队列

题目代号： 剑指 Offer 09. 用两个栈实现队列

题目描述：
用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

测试用例：
示例 1：

输入：
[“CQueue”,“appendTail”,“deleteHead”,“deleteHead”]
[[],[3],[],[]]
输出：[null,null,3,-1]
示例 2：

输入：
[“CQueue”,“deleteHead”,“appendTail”,“appendTail”,“deleteHead”,“deleteHead”]
[[],[],[5],[2],[],[]]
输出：[null,-1,null,null,5,2]

我的分析：
就创建两个栈

stack1用于入栈 stack2用于出栈

压入好说，直接压入即可
弹出就要看看stack2的情况了：如果它是空的，那就把stack1中的所有数字全部依次弹出，压入到stack2中（这样其实达到的效果就是逆序，因为咱需要的就是头节点）

那就可以弹出stack2了

代码：

class CQueue {
    //两个栈，一个出栈，一个入栈
    private Stack<Integer> stack1;
    private Stack<Integer> stack2;
    
    public CQueue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }
    
    public void appendTail(int value) {//压入是在stack1中做的
        stack1.push(value);
    }
    
    public int deleteHead() {//弹出是在stack2中做的
      
        if (stack2.isEmpty()) {
            while (!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
        } 
        // if (stack2.isEmpty()) {
        //     return -1;
        // } else {
           
        //     return stack2.pop();
        // }
        return stack2.isEmpty() ? -1 : stack2.pop();

    }
}

题目代号： 剑指 Offer 30. 包含min函数的栈

题目描述：

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

测试用例：

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.min(); --> 返回 -2.

我的分析：

举个例子把[6 2 3 4 3 1 4 7 8] 压入栈中

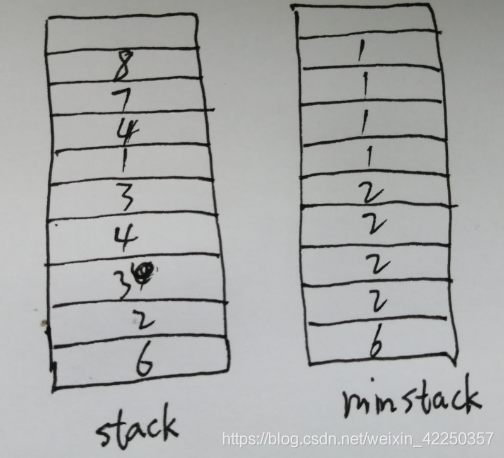
代码：

class MinStack {

    private Stack<Integer> stack;//数据栈，存放所有数据
    private Stack<Integer> minStack;//辅助栈，存放最小数据
    /** initialize your data structure here. */
    public MinStack() {
        stack=new Stack<>();
        minStack = new Stack<>(); //辅助栈
    }
    
    public void push(int x) {
        stack.push(x);
        if(minStack.empty())  //将当前最小值存入辅助栈
            minStack.push(x);//辅助栈是空的时候，就直接压入
        else
            minStack.push(x > minStack.peek() ? minStack.peek(): x);//辅助栈不是空的时候，压入最小值
            //这里是说比第一个数大的数永远不可能压入的，只压入比它小的数，比如发现1是里面的最小值，那就后面的全部压入1 1 1 1 1 
    }
    
    public void pop() {
        if(!stack.empty()){
            stack.pop();
            minStack.pop();//每个值都配套了最小值，所以每次数据栈删除元素的时候，辅助栈也要删除对应的元素
        }
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int min() {
        return minStack.peek();
    }
}

题目代号： 剑指 Offer 31. 栈的压入、弹出序列

题目描述：
输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

测试用例：

示例 1：

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2：

输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false
解释：1 不能在 2 之前弹出。

我的分析：

咱们不管怎样，来一个pushed的数先压入栈再说

那你就要看看这个压入栈的数跟popped里的数是不是相等了，如果相等的话，那就要弹出扔掉，并且i++

最后看栈是不是空就可知道是否完成任务

代码：

public boolean validateStackSequences(int[] pushed, int[] popped) {
        Stack<Integer> stack = new Stack<>();
        int i = 0;
        //为啥必须要在这里放索引，之后自加呢？是因为pushed,popped里的索引根本就不是同步的，所以只能自加
        for (int num : pushed){
            stack.push(num);//不管三七二十一，进来一个数必须先进数组
            while (!stack.isEmpty() && stack.peek() == popped[i]){
                stack.pop();//考虑栈顶元素和popped元素相等，那就弹出，并且向前
                i++;
            }

        }

        return stack.isEmpty();
    }

题目代号： 剑指 Offer 59 - II. 队列的最大值

题目描述：

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

测试用例：

示例 1：

输入:
[“MaxQueue”,“push_back”,“push_back”,“max_value”,“pop_front”,“max_value”]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]
示例 2：

输入:
[“MaxQueue”,“pop_front”,“max_value”]
[[],[],[]]
输出: [null,-1,-1]

我的分析：

就用一个数组来模拟队列，需要知道数组的起始位置和终止位置（也就是当前遍历位置）

想知道最大值，就遍历数组，取里面的最大值，这个你肯定会吧

想弹出一个元素，那就从起始位置弹出吧

想压入一个位置，那就放在终止位置之后吧

代码：

int[] queue = new int[20000];//用数组来维护一个队列
    int start = 0,end = 0;
    public MaxQueue() {

    }

    public int max_value() {//遍历一个数组拿出最大值
        int res = -1;//存放最后的最大值
        for(int i = start; i != end;i++){
            res = Math.max(res,queue[i]);
        }
        return res;
    }

    public void push_back(int value) {
        queue[end++] = value;//压入队列的时候肯定是从尾部压入的

    }

    public int pop_front() {
        if(start == end) return -1;//此时此刻，肯定是队列里面没有元素
        return queue[start++];//弹出肯定是从头部弹出的
    }