第七章 logistic回归 logistic regression

课时46 分类
二（元）分类问题是要预测的y只有0（负类negative class）或1（正类positive class）两种取值。多分类问题y有更多离散取值。
logistic regression算法：0<=hθ（x)<=1 它是一种分类算法classification algorithm，即使名字里面有回归字样。

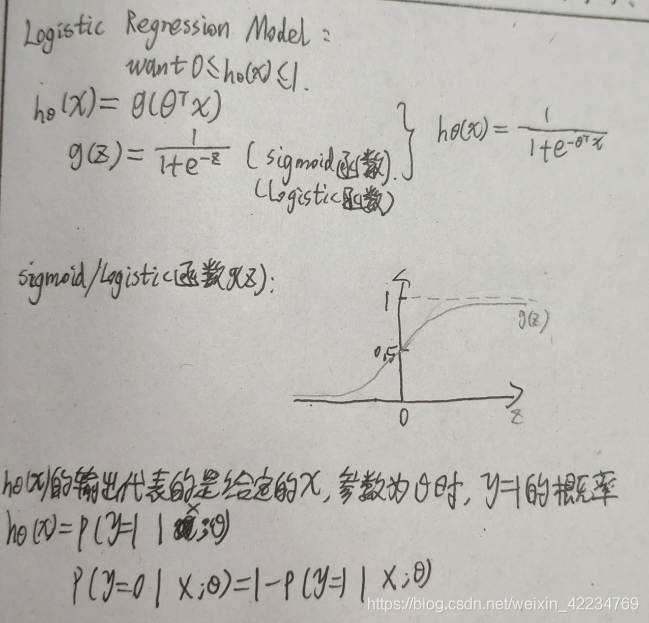
课时47 假设陈述hypothesis representation

课时48决策界限decision boundary

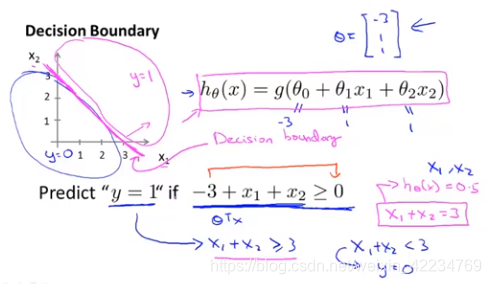
课时49 代价函数
如果按照类似线性回归的代价函数定义logistic回归的代价函数，也就是所有的模型误差的平方和，将得到一个非凹函数，也就是会有好多局部最优解，无法用梯度下降法得到全局最优解。所以需要找到更好的代价函数使其是凹函数。所以重新定义如下：

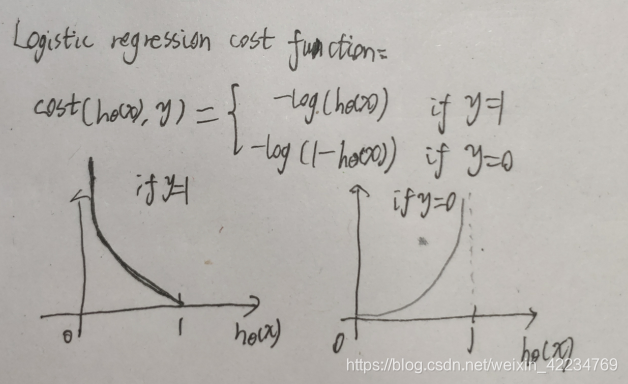
由图也可以看出，当y为1，如果预测值也等于1，则代价为0，如果预测值为0，则预测错了，代价值很大。当y为0，如果预测值也为0，则代价为0，如果预测值为1，则预测错了，用很大的代价来做了惩罚。

课时50 简化代价函数与梯度下降

简化写法：

用梯度下降算法时，feature scaling同样适用于logistic regression。

课时51 高级优化
如果能编程计算出J（θ）和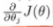，有更优化的算法如下图来替代梯度下降算法，不再需要手动选择学习率，收敛速度也更快，不需要搞清楚具体算法内部的循环，直接调库会用就行了。

实现方法：

在octave上实现：


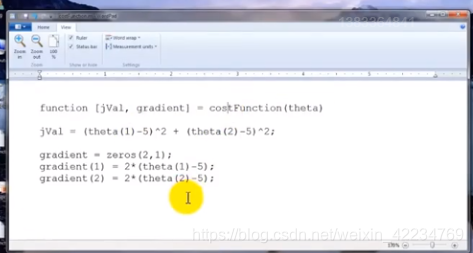
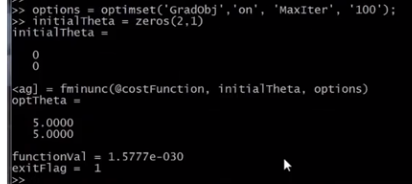
exitFlag为1表示已经收敛

当有一个很大的机器学习问题时，应该用这些高级优化算法而不是梯度下降，速度更快。

课时52 多元分类：一对多


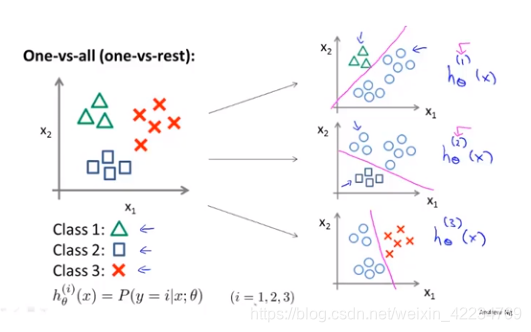
（1）代表以class 1作为正类，其他是负类，以此类推。