参考博客:人工智能搜索策略:A*算法
1.A 算法
在图搜索算法中,如果能在搜索的每一步都利用估价函数f(n)=g(n)+h(n)对Open表中的节点进行排序,则该搜索算法为A算法。由于估价函数中带有问题自身的启发性信息,因此,A算法又称为启发式搜索算法。
对启发式搜索算法,又可根据搜索过程中选择扩展节点的范围,将其分为全局择优搜索算法和局部择优搜索算法。
`
1.1.全局择优算法
在全局择优搜索中,每当需要扩展节点时,总是从Open表的所有节点中选择一个估价函数值最小的节点进行扩展。其搜索过程可能描述如下:
(1)把初始节点S0放入Open表中,f(S0)=g(S0)+h(S0);
(2)如果Open表为空,则问题无解,失败退出;
(3)把Open表的第一个节点取出放入Closed表,并记该节点为n;
(4)考察节点n是否为目标节点。若是,则找到了问题的解,成功退出;
(5)若节点n不可扩展,则转到第(2)步;
(6)扩展节点n,生成子节点ni(i=1,2,……),计算每一个子节点的估价值f(ni) (i=1,2,……),并为每一个子节点设置指向父节点的指针,然后将这些子节点放入Open表中;
(7)根据各节点的估价函数值,对Open表中的全部节点按从小到大的顺序重新进行排序;
(8)转第(2)步。
由于上述算法的第(7)步要对Open表中的全部节点按其估价函数值从小到大重新进行排序,这样在算法第(3)步取出的节点就一定是Open表的所有节点中估价函数值最小的一个节点。因此,它是一种全局择优的搜索方式。
对上述算法进一步分析还可以发现:
如果取估价函数f(n)=g(n),则它将退化为代价树的广度优先搜索;
如果取估价函数f(n)=h(n),则它将退化为广度优先搜索。
可见,广度优先搜索和代价树的广度优先搜索是全局择优搜索的两个特例。
1.1.1.求解八数码
例 1: 八数码难题。 设问题的 初始状态S0 和 目标状态Sg 如图所示,估价函数与请用全局择优搜索解决该题。
图1 八数码难题的全局择优搜索树
1.2.局部择优算法
在局部择优搜索中,每当需要扩展节点时,总是从刚生成的子节点中选择一个估价函数值最小的节点进行扩展。其搜索过程可描述如下:
(1)把初始节点S0放入Open表中,f(S0)=g(S0)+h(S0);
(2)如果Open表为空,则问题无解,失败退出;
(3)把Open表的第一个节点取出放入Closed表,并记该节点为n;
(4)考察节点n是否为目标节点。若是,则找到了问题的解,成功退出;
(5)若节点n不可扩展,则转到第(2)步;
(6)扩展节点n,生成子节点ni(i=1,2,……),计算每一个子节点的估价值f(ni) (i=1,2,……),并 按估价值从小到大的顺序依次放入Open表的首部(不是全部排序,而是这个扩展节点n生成的子节点),并为每一个子节点设置指向父节点的指针,然后转第(2)步。
由于这一算法的第六步仅仅是把刚生成的子节点按其估价函数值从小到大放入Open表中,这样在算法第(3)步取出的节点仅是刚生成的子节点中估价函数值最小的一个节点。因此,它是一种局部择优的搜索方式。
对这一算法进一步分析也可以发现:
如果取估价函数f(n)=g(n),则它将退化为代价树的深度优先搜索;
如果取估价函数f(n)=d(n),则它将退化为深度优先搜索。
可见,深度优先搜索和代价树的深度优先搜索是局部择优搜索的两个特例。
1.2.1.求解八数码
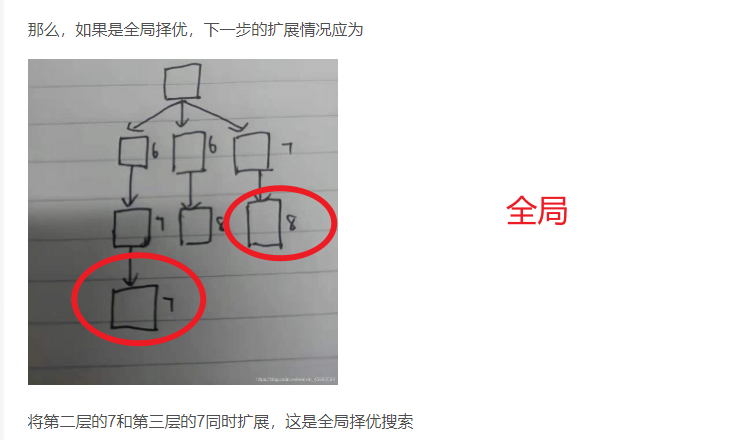
和用全局择优算法一样(估价函数一样),但扩展的顺序不一样
局部更类似深度,全局跟类似广度
如下图片可体现区别:
在此仅画出权重f(x),对于八数码的各个变化不再详细画出。
2.A*算法
上一节讨论的启发式搜索算法,都没有对估价函数f(n)做任何限制。实际上,估价函数对搜索过程是十分重要的,如果选择不当,则有可能找不到问题的解,或者找到的不是问题的最优解。为此,需要对估价函数进行某些限制。A* 算法就是对估价函数加上一些限制后得到的一种启发式搜索算法。
假设f*(n)为从初始节点S0出发,约束经过节点n到达目标节点的最小代价值。估价函数f(n)则是f*(n)的估计值。
显然,f*(n)应由以下两部分所组成:
- 一部分是从初始节点S0到节点n的最小代价,记为g*(n);
- 另一部分是从节点n到目标节点的最小代价,记为h*(n),当问题有多个目标节点时,应选取其中代价最小的一个。
因此有 f*(n)=g*(n) +h*(n)
把估价函数f(n)与 f*(n)相比
- g(n)是对g*(n)的一个估计
- h(n)是对h*(n)的一个估计。

则称得到的算法为A*算法。
2.1 解决八数码难题
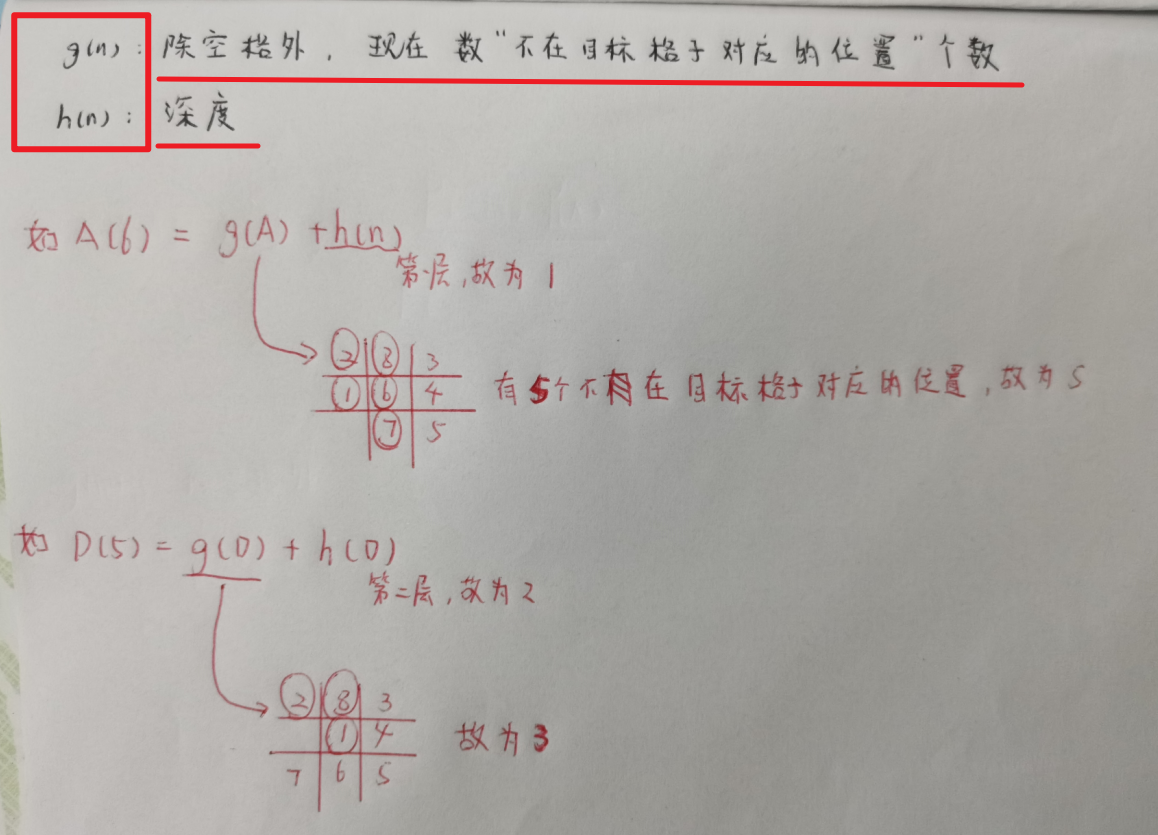
g*(n)为起点到n状态的最短路径代价值;换句话说,就是层数
h*(n)是n状态到目的状态的最短路径的代价值。换句话说,“不在位”数码个数至少要移动多少位才能变成目标数码对应的位置
这样,f*(n)就是起点出发通过n状态而到达目的状态的最佳路径的总代价值。
在该图中,从这些值还可以看出,最佳路径上的节点都有 f*=g*+h*=4.








 本文详细介绍了A算法的全局与局部择优搜索策略,以及A*算法的原理。通过八数码难题为例,展示了两种算法在解决问题时的不同策略,全局择优搜索类似于广度优先,局部择优更接近深度优先。A*算法通过对估价函数的限制,确保找到最优解。在解决八数码问题时,A*算法结合实际代价值和启发式信息,找到最佳路径。
本文详细介绍了A算法的全局与局部择优搜索策略,以及A*算法的原理。通过八数码难题为例,展示了两种算法在解决问题时的不同策略,全局择优搜索类似于广度优先,局部择优更接近深度优先。A*算法通过对估价函数的限制,确保找到最优解。在解决八数码问题时,A*算法结合实际代价值和启发式信息,找到最佳路径。























 2315
2315

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










