切面条问题

 题目介绍：

一根高筋拉面，中间切一刀，可以得到2根面条。

如果先对折1次，中间切一刀，可以得到3根面条。

如果连续对折2次，中间切一刀，可以得到5根面条。 那么，连续对折10次，中间切一刀，会得到多少面条呢？

---

题目分析：

 

 

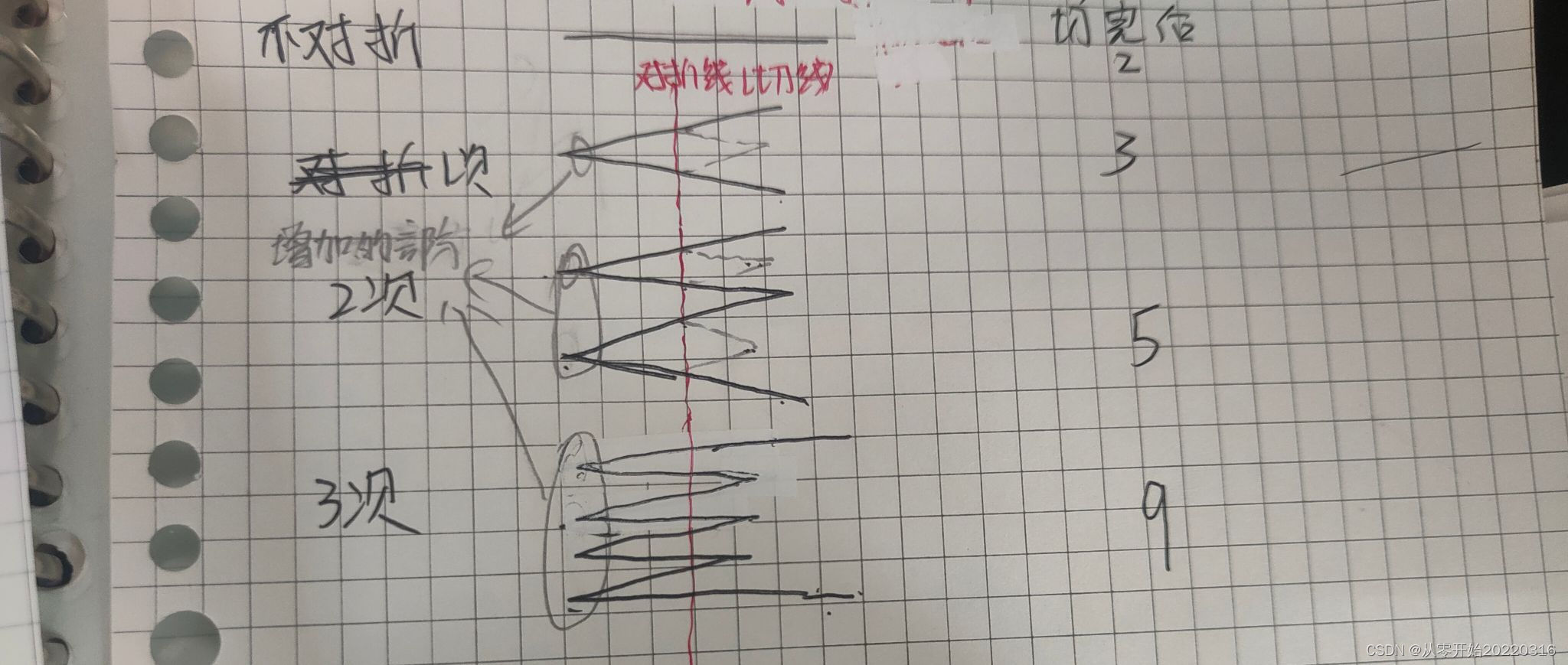
        需要借助图形辅助分析，根据图像很容易发现对折实际上是将左边尖端部分对折，切一刀的行为 等价于 去数端点的个数，不难发现每次增加的部分就是对折完后，左边尖尖的部分，由此可发现每次增加的端点个数为2的n次幂。

---

代码结果： 

                              

 

---

解法一：

算法思路：

1、不对折（对折零次），从中间切一刀，得到 2 根面条， 2 = 2
2、对折一次，从中间切一刀，得到 3 根面条， 3 = 2 + 2^0
3、对折两次，从中间切一刀，得到 5 根面条， 5 = 2 + 2^0 + 2^1
4、对折三次，从中间切一刀，得到 9 根面条， 9 = 2 + 2^0 + 2^1 + 2^2
…
11、对折十次，从中间切一刀，得到 2 + 2^0 + 2^1 + 2^2 + ...... + 2^9 根面条

代码实现:

a = 2
for i in range(0,10):
    a = a + 2**i
    print (a)

---

同类型题：