
Floyd算法:
思路 :遍历计算 i 点 经过 k 点 到 j 点 的最小路径值 (动态规划思路)
缺点:时间复杂度高,不能解决负边情况
输入样例:
4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12
输出样例:
1-->2:2
1-->3:5
1-->4:4
2-->1:9
2-->3:3
2-->4:4
3-->1:6
3-->2:8
3-->4:1
4-->1:5
4-->2:7
4-->3:10
#include #include#include#include#include#include#include
using namespacestd;const int inf=0x7fffff;const long long mod=1e9+7;const double PI=acos(-1);intn,m,start,end;int ans=9999999;bool vis[105];int e[105][105];void init(){ //初始化邻接矩阵
for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j) e[i][j]=0;else e[i][j]=inf;
}
}
}void Floyd(){ //思路:依此判断 i 通过 k 到 j 的最短路
for(int k=1;k<=n;k++){ //k 经转的节点
for(int i








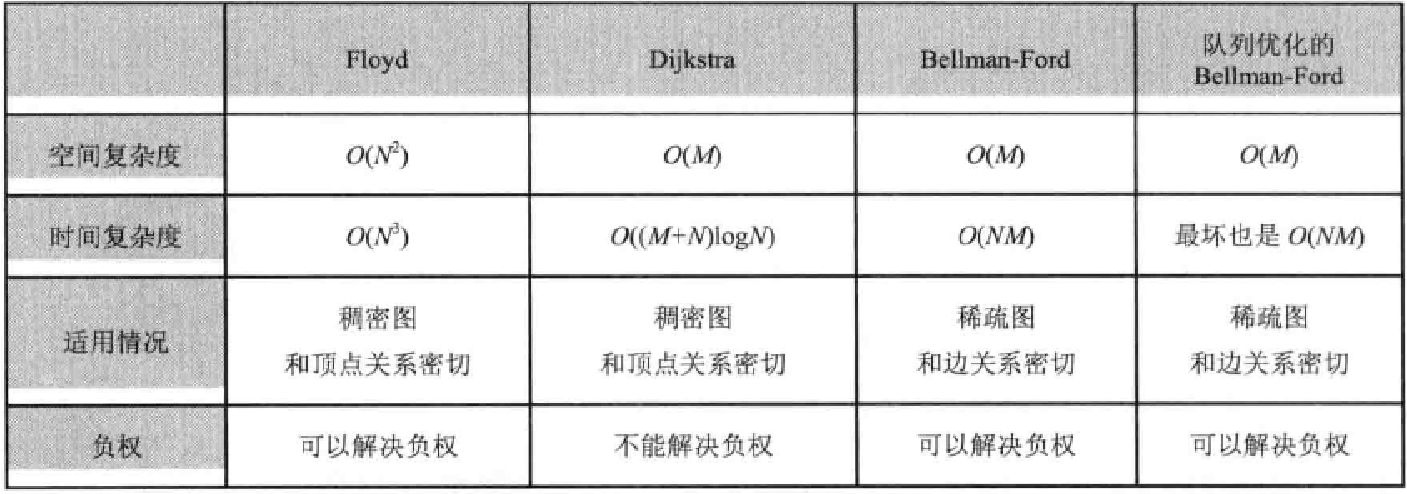
 本文介绍了三种Java实现的最短路径算法:Floyd算法,Dijkstra算法和Bellman-Floyd算法。Floyd算法通过动态规划遍历所有节点寻找最短路径,但不适用于负边。Dijkstra算法从起点开始逐次找到最短路径。Bellman-Floyd算法能处理负边情况,通过n-1次迭代更新最短路径。
本文介绍了三种Java实现的最短路径算法:Floyd算法,Dijkstra算法和Bellman-Floyd算法。Floyd算法通过动态规划遍历所有节点寻找最短路径,但不适用于负边。Dijkstra算法从起点开始逐次找到最短路径。Bellman-Floyd算法能处理负边情况,通过n-1次迭代更新最短路径。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








