二元函数洛必达求极限_高等数学（微积分）极限求法大全

高等数学里, 求极限的技巧特别多, 这也正是因为极限的求法相对比较难, 所以发展出多种多样的求极限方法. 有很多方法只是针对特定类型的极限有效. 现在我们看看高等数学里都有哪些求极限的方法, 以及哪些类型的极限应用什么方法比较有效.

我们先来说一说求极限时的一般原则.

1. 首先, 运用极限的运算法则(四则运算, 连续函数的极限, 复合函数的极限), 确定极限是不是未定式极限；

2. 两种基本的未定式极限是 0/0 和 型, 这两种情形一般可以用洛必达法则来求. 有一些特殊的情形, 我们接下来讲；

3. 其它未定式极限,要先化成上面的两种基本情形来求，然后用洛必达法则或者其它方法来求。

各种类型的极限求法:

1. 对未定式极限，0/0 型或者 ，最有效也是最基本的方法是洛必达法则。也就是在求极限的时候，先分子分母分别求导，再求极限。例如

2. 0/0 型， ，且分子分母都是多项式，则分子分母可以约去无穷小因子 。

3. 0/0 型， ，且分子或者分母有根式， 则先对根式有理化，然后用极限运算法则或者约去无穷小因子的方法来计算。

4. 0/0 型， ，分子或分母有三角函数，则利用三角函数恒等式或其它变换，化成两个重要极限的第一个，利用那个极限来求。

5. 型， (或者 )，且分子分母都是 x (或者 n)的多项式或者类似于多项式(根式里是多项式)时，分子分母同除以 x 的最高阶幂。

6. 型，如二者都是分式，则先通分，化成两种基本形式，再用洛必达法则或者其它方法求极限。

7. 型，如果其中一个含有根式，则先有理化，再用其它方法求极限。

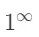8. 型 ， 首先尝试能不能化成 的复合式，然后利用已知极限 , 这里 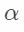是一个无穷小量。

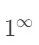9. 型， 型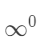， 型，先取对数， 再取 e 底，化成基本的未定式极限 ，然后用洛必达法则或者其它方式求极限。例如最后一步是对指数部分应用洛必达法则。

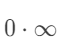10. 型，将其中一个乘式变成分母，从而化成两种基本形式的未定式；再利用其它方法求积分。例如

11. 如果未定式极限里，函数比较复杂，不能用洛必达法则或者洛必达法则使用起来太麻烦的话，则考虑用泰勒展开来求极限。例如
    前者将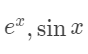 展开到三阶，后者将 展开到 的四阶。

12. 如果可以通过一个明显的放缩，且放缩后两者的极限都相等的话，就使用夹挤原理来求极限。例如
    显然有
    不等号的左边和右边都有相同极限 1(只需要在分子分母除以  即可)，所以由夹挤原理，原极限为 1。

13. 如果含有变上限积分，那么通常情况下是洛必达法则结合变上限积分的导数来求；

14. 如果数列是用递推或者迭代形式给出， 即 ， 那么肯定是用递推法来求极限，这时候，要注意，一定要先证明极限存在(单调有界数列)，然后两边取极限，可得一个代数式，从而可以求得极限；

15. 如果是数列的每一项是无限多个项相加，且每一项可以写成 的话，那么这个极限可以用定积分的定义来求。这里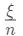， 取值范围就是定积分的积分上下限，而  就是被积函数。例如
    这里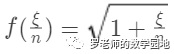， ，所以被积函数是 ， 在和式里的取值范围是从 0 到 1。(0 这一项可以认为没写出来)。所以原极限等于定积分

    

16. 分段函数在分段点处的极限一定要求左右极限，然后确定二者是否相等；

17. 幂指函数 的极限，如果是未定式极限， 一定要先化成 形式，然后运用复合函数的极限法则，将极限符号移到指数上去，对指数部分用未定义极限的求法求极限。也就是说