05-密码学基础-RSA的介绍

1、什么是RSA？

RSA是一种公钥密码算法，它的名字由三位开发者，即Ron Rivest、Adi Shamir和Leonard Adleman的姓氏的首字母组成的。 RSA被用于公钥密码和数字签名。 1983年，RSA公司为RSA算法在美国取得了专利，但现在该专利已经过期。

2、算法原理介绍

step	说明	描述	备注
1	找出质数	P 、Q	-
2	计算公共模数	N = P * Q	-
3	欧拉函数	φ(N) = (P-1)(Q-1)	-
4	计算公钥E	1 < E < φ(N)	E的取值必须是整数 E 和 φ(N) 必须是互质数
5	计算私钥D	E * D % φ(N) = 1	-
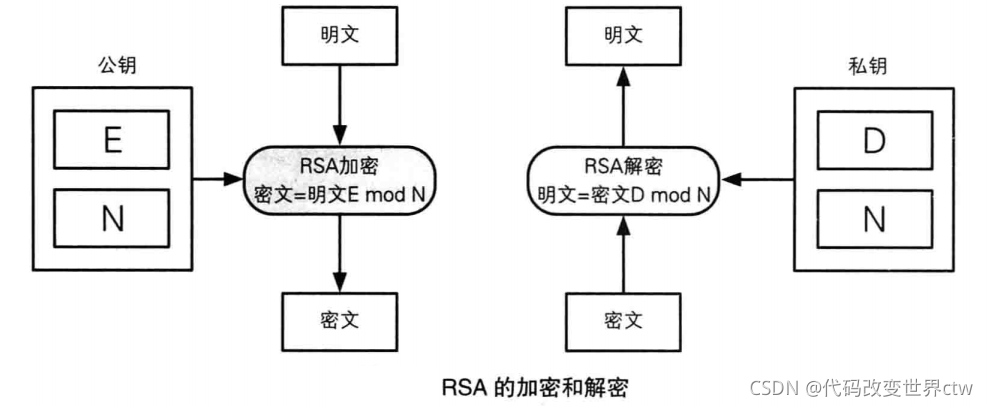
6	加密	C ＝ ME mod N	C：密文 M：明文
7	解密	M ＝CD mod N	C：密文 M：明文

3、算法举例

• 随机选择两个不相等的质数 : p=61、q=53
• 计算 n = p × q = 61×53 = 3233
• 计算n的欧拉函数 : φ(n) = (p-1)(q-1) = 3120
• 随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质, 我们选择一个 e=17
• 计算e对于φ(n)的模反元素d ： d*e%φ(n)=1

支持 n e d都算出来了，n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）

公钥能否推导出私钥，也就是n和e的情况下，推导出d

• （1）ed%φ(n)=1, 推导d, 需要知道e和φ(n)
• （2）φ(n)=(p-1)(q-1)。计算φ(n), 需要知道p和q
• （3）n=pq。只有将n因数分解，才能算出p和q.

私钥能否推导出公钥，也就是n和d的情况下，推导出e

• （1）ed%φ(n)=1, 推导e, 需要知道d和φ(n)
• （2）φ(n)=(p-1)(q-1)。计算φ(n), 需要知道p和q
• （3）n=pq。只有将n因数分解，才能算出p和q.

对于3233您可以进行因数分解（3233=61×53），那么对于下面一个这样很大的数字呢？

12301866845301177551304949
　　58384962720772853569595334
　　79219732245215172640050726
　　36575187452021997864693899
　　56474942774063845925192557
　　32630345373154826850791702
　　61221429134616704292143116
　　02221240479274737794080665
　　351419597459856902143413

它等价于：

33478071698956898786044169
　　84821269081770479498371376
　　85689124313889828837938780
　　02287614711652531743087737
　　814467999489
　　　　×
　　36746043666799590428244633
　　79962795263227915816434308
　　76426760322838157396665112
　　79233373417143396810270092
　　798736308917

公钥(e,n)对明文m进行加密 ： c = m^e % n
私钥(d,n)对密文c进行解密 ： m = c^d % n

其中e和d是对等的，一样的地位，可以互换的. 所以，公钥推出私钥比较困难，那么私钥推出公钥也是比较困难.
另外，在密码学中，我们一般不说通过公钥并不是完全不能推算出私钥， 而是表述为：通过公钥推算私钥在计算上是困难的。

那么为什么我们在平时使用时，感觉的是公钥不能推导私钥，但私钥可以推导公钥呢？
因为在PEM或DER的编码格式中，公钥包含了N和E，私钥包含了N E D P Q等信息，也就是私钥已经包含了公钥，故私钥是能推出公钥的。
另外在通常使用中，e一般就等于65535，所以无需推导.

4、RSA的用法

公钥加密、私钥解密
私钥签名、公钥验签