面试题33-二叉搜索树的后序遍历序列

题目：

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

方法一：递归

二叉搜索树的特点是左子树的值<根节点<右子树的值。而后续遍历的顺序是：

左子节点→右子节点→根节点；

比如下面这棵二叉树，他的后续遍历是

[3，5，4，10，12，9]

我们知道后续遍历的最后一个数字一定是根节点，所以数组中最后一个数字9就是根节点，我们从前往后找到第一个比9大的数字10，那么10后面的[10，12]（除了9）都是9的右子节点，10前面的[3，5，4]都是9的左子节点，后面的需要判断一下，如果有小于9的，说明不是二叉搜索树，直接返回false。然后再以递归的方式判断左右子树。

再来看一个，他的后续遍历是[3，5，13，10，12，9]

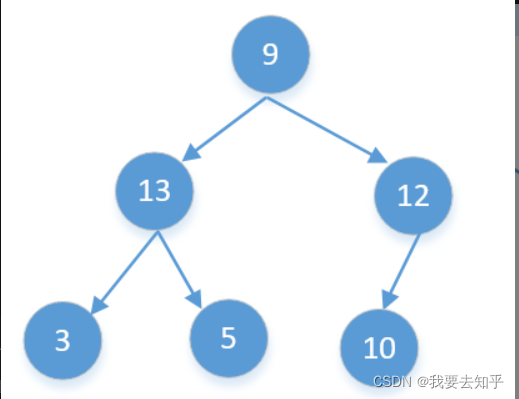
我们来根据数组拆分，第一个比9大的后面都是9的右子节点[13，10，12]。然后再拆分这个数组，12是根节点，第一个比12大的后面都是12的右子节点[13，10]，但我们看到10是比12小的，他不可能是12的右子节点，所以我们能确定这棵树不是二叉搜索树。搞懂了上面的原理我们再来看下代码。

class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        int n=postorder.size();
       return helper(postorder,0,n-1);
    }
    bool helper(vector<int>& postorder,int left,int right)
    {
    	//如果left==right，就一个节点不需要判断了，如果left>right说明没有节点，
   		//也不用再看了,否则就要继续往下判断
        if(left>=right)
            return true;
        //找根节点
        int root=postorder[right],mid=left;
        // int i=left;
        // for(;i<right;++i)
        // {
        //     if(postorder[i]>root)
        //     {
        //         mid=i;
        //         break;
        //     }
              
        // }
        // mid=i;  
        //对上面for循环的简化
        while(postorder[mid]<root)
        	mid++;//mid必须跟着一起移动到下一位
        for(int i=mid;i<right;++i)
        {
            if(postorder[i]<root)
                return false;
        }        
       
        return helper(postorder,left,mid-1)&&helper(postorder,mid,right-1);    
    }
};

1. 时间复杂度：O（n^2），递归占用O（n），当树退化为链表的时候，每次递归需要遍历n个节点
2. 空间复杂度：O（n），最差情况下（即当树退化为链表），递归深度将达到 n。

方法二：栈

我们先来画一个节点多一些的二叉搜索树，然后观察一下他的规律

他的后续遍历结果是

[3,6,5,9,8,11,13,12,10]

从前往后不好看，我们来从后往前看

[10,12,13,11,8,9,5,6,3]

如果你仔细观察会发现一个规律，就是挨着的两个数如果arr[i]<arr[i+1]，那么arr[i+1]一定是arr[i]的右子节点，这一点是毋庸置疑的，我们可以看下上面的10和12是挨着的并且10<12，所以12是10的右子节点。同理12和13，8和9，5和6，他们都是挨着的，并且前面的都是小于后面的，所以后面的都是前面的右子节点。如果想证明也很简单，因为比arr[i]大的肯定都是他的右子节点，如果还是挨着他的，肯定是在后续遍历中所有的右子节点最后一个遍历的，所以他一定是arr[i]的右子节点。

我们刚才看的是升序的，再来看一下降序的（这里的升序和降序都是基于后续遍历从后往前看的，也就是上面蓝色数组）。如果arr[i]>arr[i+1]，那么arr[i+1]一定是arr[0]……arr[i]中某个节点的左子节点，并且这个值是大于arr[i+1]中最小的。我们来看一下上面的数组，比如13，11是降序的，那么11肯定是他前面某一个节点的左子节点，并且这个值是大于11中最小的，我们看到12和13都是大于11的，但12最小，所以11就是12的左子节点。同理我们可以观察到11和8是降序，8前面大于8中最小的是10，所以8就是10的左子节点。9和5是降序，6和3是降序，都遵守这个规律。

根据上面分析的过程，很容易想到使用栈来解决。遍历数组的所有元素，如果栈为空，就把当前元素压栈。如果栈不为空，并且当前元素大于栈顶元素，说明是升序的，那么就说明当前元素是栈顶元素的右子节点，就把当前元素压栈，如果一直升序，就一直压栈。当前元素小于栈顶元素，说明是倒序的，说明当前元素是某个节点的左子节点，我们目的是要找到这个左子节点的父节点，就让栈顶元素出栈，直到栈为空或者栈顶元素小于当前值为止，其中最后一个出栈的就是当前元素的父节点（注：栈中的元素按升序排列的，最后的出栈的元素是刚好小于当前元素的）。我们来看下代码

class Solution {
public:
    vector<int>arr1,arr2;
    bool verifyPostorder(vector<int>& postorder) {
    stack<int> s;
    int parent = INT_MAX;
    //注意for循环是倒叙遍历的
    for (int i = postorder.size() - 1; i >= 0; i--) {
        int cur = postorder[i];
        //当如果前节点小于栈顶元素，说明栈顶元素和当前值构成了倒叙，
        //说明当前节点是前面某个节点的左子节点，我们要找到他的父节点
        while (!s.empty() && s.top() > cur)
        {
            parent = s.top();
            s.pop();
        }

        //只要遇到了某一个左子节点，才会执行上面的代码，才会更
        //新parent的值，否则parent就是一个非常大的值，也就
        //是说如果一直没有遇到左子节点，那么右子节点可以非常大
        if (cur > parent)
            return false;
        //入栈
        s.push(cur);
    }
    return true;
    }
};

1. 时间复杂度：O（n）
2. 空间复杂度：O（n），退化为链表的时候空间复杂度最高