面试题63-股票的最大利润

题目

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

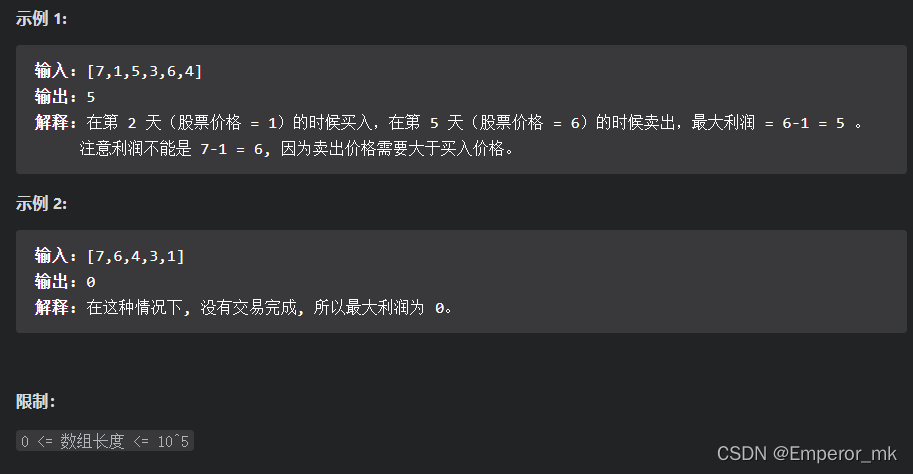
方法一：遍历数组

我们可以先定义函数diff（x）为当卖出价位数组中第i个数字时可能获得的最大利润。显然，在卖出价固定时，买入价越低获得的利润越大。也就是说如果在扫描到数组中的第i个数字时，只要我们能够记住之前的i-1个数字中的最小值，就能算出在当前价位卖出时可能得到的最大利润。

class Solution {
   
public:
    int maxProfit(vector<int>& prices) {
   
        int n=prices.size();
        if(n<2)
            return 0;
        int min=prices[0];
        int maxDiff=prices[1]-min;
        for(int i=2;i<n;++i)
        {
   
            if(prices[i-1]<min)
                min=prices[i-1];//刨除最后一个元素最小的情况
            int currentDiff=prices[i]-min;
            if(currentDiff>maxDiff)
                maxDiff=currentDiff;
        }
        return maxDiff<0?0:maxDiff;
    }
};

1. 时间复杂度：O（n）
2. 空间复杂度：O（1）

方法二：动态规划

初步分析

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max( 今天选择 rest,        今天选择 sell       )
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max( 今天选择 rest,         今天选择 buy         )

状态转移方程

base case：
dp[-1][...][0] = dp[...][0][0] = 0
dp[-1][...][1] = dp[...][0][1] = -infinity

状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

套用状态转移方程

dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i]) 
            = max(dp[i-1][1][1], -prices[i])
解释：k = 0 的 base case，所以 dp[i-1][0][0] = 0。

现在发现 k 都是 1，不会改变，即 k 对状态转移已经没有影响了。
可以进行进一步化简去掉所有 k：
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i]