9 单变量线性回归-深度学习应用开发-TensorFlow实践

最新推荐文章于 2021-10-06 17:00:27 发布

Irain_Luo

最新推荐文章于 2021-10-06 17:00:27 发布

阅读量485

点赞数

分类专栏： # TensorFlow基础学习文章标签： python tensorflow 机器学习

本文链接：https://blog.youkuaiyun.com/weixin_42122125/article/details/107598000

版权

TensorFlow基础学习专栏收录该内容

8 篇文章

订阅专栏

作者：Irain
QQ：2573396010
微信：18802080892
GitHub资源链接：https://github.com/Irain-LUO/Tensorflow-learner
教学视频链接：第五讲单变量线性回归：TesnsorFlow实战
详细文档链接：第四章单变量线性回归：TesnsorFlow实战

1 应用描述

在这里插入图片描述
应用内容:如上分布图所示，数据散点图的分布情况接近一条直线，每个数据只有一个因变量和自变量，以某种线性关系构成X-Y数轴。我们希望算出数据间的线性关系，获得一条最优直线，来拟合散点图上的数据。
涉及技术点：numpy库（准备训练模型的数据）、matplotlib库（描绘数据散点图、模型线性图）、tensorflow库（训练模型，获得最佳模型参数）、SGD随机梯度下降优化。

2 实现过程

2.1 核心步骤

使用TensorFlow进行算法设计与训练有以下四个核心步骤：

准备数据
构建模型
训练模型
进行预测

上述步骤是我们使用TensorFlow进行算法设计和训练的核心步骤，贯穿于后面介绍的具体实战中。

2.2 核心步骤具体内容

2.2.1 准备数据

导入第三方库（matplotlib、numpy、tensorflow），设置随机种子。

#在Jupyter中，使用matplotlib显示图像需要设置为 inline 模式，否则不会现实图像
%matplotlib inline
import matplotlib.pyplot as plt # 载入matplotlib
import numpy as np # 载入numpy
import tensorflow as tf # 载入Tensorflow
# https://numpy.org/doc/1.18/reference/random/generated/numpy.random.seed.html?highlight=seed
np.random.seed(5) # 设定随机种子

使用numpy.linspace()方法，以等差数列的方式，在-1~1之间产生100个数据点。

#直接采用np生成等差数列的方法，生成100个点，每个点的取值在-1~1之间
# https://numpy.org/doc/1.18/reference/generated/numpy.linspace.html
x_data = np.linspace(-1, 1, 100)

在这里插入图片描述
使用np.random.randn(*x_data.shape) * 0.4，随机产生y=2x+1线性关系的噪音数据。

# y = 2x +1 + 噪声， 其中，噪声的维度与x_data一致
# https://numpy.org/doc/1.18/reference/random/generated/numpy.random.randn.html?highlight=randn#numpy-random-randn
y_data = 2 * x_data + 1.0 + np.random.randn(*x_data.shape) * 0.4

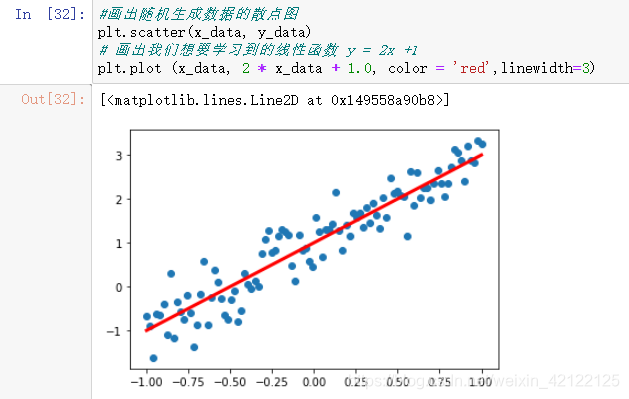
在这里插入图片描述
使用pyplot（scatter、plot）画出随机生成数据的散点图和线性函数 y = 2x +1的直线。

#画出随机生成数据的散点图
plt.scatter(x_data, y_data) 
# 画出我们想要学习到的线性函数 y = 2x +1
plt.plot (x_data, 2 * x_data + 1.0, color = 'red',linewidth=3)

在这里插入图片描述

2.2.2 构建模型

定义训练数据的占位符，x是特征值，y是标签值。

# 定义训练数据的占位符，x是特征值，y是标签值
# https://tensorflow.google.cn/api_docs/python/tf/compat/v1/disable_eager_execution?hl=en
tf.compat.v1.disable_eager_execution()
# https://tensorflow.google.cn/api_docs/python/tf/compat/v1/placeholder?hl=en
x = tf.compat.v1.placeholder("float", name = "x") # tf.placeholder() is not compatible with eager execution.
y = tf.compat.v1.placeholder("float", name = "y")

接下来定义模型函数-线性函数y = w*x + b。

def model(x, w, b):
    return tf.multiply(x, w) + b

接下来我们创建模型的变量，Tensorflow变量的声明函数是tf.Variable，tf.Variable的作用是保存和更新参数，变量的初始值可以是随机数、常数或是通过其他变量的初始值计算得到。

# 构建线性函数的斜率，变量w
w = tf.Variable(1.0, name="w0")
# 构建线性函数的截距，变量b
b = tf.Variable(0.0, name="b0")   
# pred是预测值，前向计算
pred = model(x, w, b)

定义一些超参数，包括训练的轮数和学习率。其中如果学习率设置过大，可能导致参数在极值附近来回摇摆，无法保证收敛。如果学习率设置过小，虽然能保证收敛，但优化速度会大大降低，我们需要更多迭代次数才能达到较理想的优化效果。

# 迭代次数（训练轮数）
train_epochs = 10
# 学习率
learning_rate = 0.05 
# 控制显示loss值的粒度
display_step = 10

定义损失函数和优化器。损失函数用于描述预测值与真实值之间的误差，从而指导模型收敛方向。

# 采用均方差作为损失函数
loss_function = tf.reduce_mean(tf.square(y-pred))  
# 梯度下降优化器
# https://tensorflow.google.cn/api_docs/python/tf/compat/v1/train/GradientDescentOptimizer?hl=en
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

声明会话及初始化。

sess = tf.compat.v1.Session()
init = tf.compat.v1.global_variables_initializer()
sess.run(init)

2.2.3 训练模型

模型训练阶段，设置迭代轮次，每次通过将样本逐个输入模型，进行梯度下降优化操作，每轮迭代后，绘制出模型曲线。将每一轮的训练损失值都显示出来。

# 开始训练，轮数为 epoch，采用SGD随机梯度下降优化方法
step = 0   # 记录训练步数
loss_list = []   # 用于保存loss值的列表
for epoch in range(train_epochs):
    for xs,ys in zip(x_data, y_data):
        _, loss=sess.run([optimizer,loss_function], feed_dict={x: xs, y: ys}) 
         # 显示损失值 loss
        # display_step：控制报告的粒度
        # 例如，如果 display_step 设为 2 ，则将每训练2个样本输出一次损失值
        # 与超参数不同，修改 display_step 不会更改模型所学习的规律
        loss_list.append(loss)
        step=step+1
        if step % display_step == 0:
            print("Train Epoch:", '%02d' % (epoch+1), "Step: %03d" % (step),"loss=", \
                  "{:.9f}".format(loss))
                
    b0temp=b.eval(session=sess)
    w0temp=w.eval(session=sess)
    plt.plot (x_data, w0temp * x_data + b0temp  )# 画图
plt.scatter(x_data, y_data)

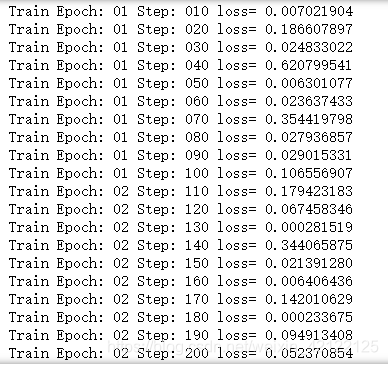
在这里插入图片描述

从上图可以看出，本案例所拟合的模型较简单，训练3次之后已经接近收敛对于复杂模型，需要更多次训练才能收敛。

2.2.4 进行预测

设定x测试值（x=1），使用刚刚的训练模型，预测结果。

x_test = 1
predict = sess.run(pred, feed_dict={x: x_test})
print("预测值：%f" % predict)
target = 2 * x_test + 1.0
print("目标值：%f" % target)

在这里插入图片描述
上述图，可以预测值和目标值接近，误差近3%。不是所有的x值的误差都在3%内，有些误差较大。

2.2.5 记录计算图

生成- - 个写日志的writer,并将当前的TensorFlow计算图写入日志。

logdir = './log'
#生成- - 个写日志的writer,并将当前的TensorFlow计算图写入日志。
#https://tensorflow.google.cn/api_docs/python/tf/compat/v1/summary/FileWriter?hl=en
writer = tf.compat.v1.summary.FileWriter(logdir, tf.compat.v1.get_default_graph())
writer.close()

在这里插入图片描述

3 总结

小编从三个方面来讲：学习难度、意义、缺陷。
教学视频选择了这个比较简单的Tensorflow应用，来深入了解Tensoflow的实践。
这个意义对我来是关键的，在Tensorflow方面质的飞跃，从理论在实践（数据准备、训练模型）。
自己有不能独立完成的严重缺陷。刚入门的初学者都有这些不足，需要长时间地学习和独立尝试。