python 凯利公式_蒙特卡罗方法验证凯利公式

说明

本文受知乎陈小米启发而写。有兴趣的朋友可以移步这里。

本文的代码完全是本人所撸。

问题描述

假想一个游戏。赢的概率是60%，输的概率40%。入场费随意交。如果赢了获得2倍的入场费金额(1赔1)，输则输掉入场费。小米有1000元做本金，请问小米每次给多少入场费，理论上100次游戏后几何期望收益能最大？

【本人的疑问】为何这里考虑几何期望，而不是数学期望？【已解决，见代码注释！】

凯利公式

\[f=p-\frac{q}{b}

\]

不多说，上代码。

完整代码

import pandas as pd

import numpy as np

import random

import matplotlib.pyplot as plt

'''

用蒙特卡罗方法，验证凯利公式的计算得到资金比例是不是最佳的

参考：https://zhuanlan.zhihu.com/p/20849995

'''

pwin = 0.6 # 胜率

b = 1 # 净赔率

# 凯利值

def kelly(pwin, b):

'''

参数

pwin 胜率

b 净赔率

返回

f 投注资金比例

'''

f = (b * pwin + pwin - 1) / b

return f

# 游戏

def play_game(f, cash=100, m=100):

global pwin, b

res = [cash]

for i in range(m):

if random.random() <= pwin:

res.append(res[-1] + int(f*res[-1])*b)

else:

res.append(res[-1] - int(f*res[-1]))

return res

# 蒙特卡罗方法重复玩游戏

def montecarlo(n=1000, f=0.15, cash=1000, m=100):

res = []

for i in range(n):

res.append(play_game(f, cash, m))

#return pd.DataFrame(res).sum(axis=0) / n #【 数学期望】不平滑

return np.exp(np.log(pd.DataFrame(res)).sum(axis=0) / n) # 【几何期望】平滑

n = 1000 # 重复次数

cash = 1000 # 初始资金池

m = 100 # 期数

f = 0.1 # 资金比例 10%

res1 = montecarlo(n, f, cash, m)

fk = kelly(pwin, b) # 资金比例 凯利值

res2 = montecarlo(n, fk, cash, m)

f = 0.5 # 资金比例 50%

res3 = montecarlo(n, f, cash, m)

f = 1.0 # 资金比例 100%

res4 = montecarlo(n, f, cash, m)

# 画个图看看

fig = plt.figure()

axes = fig.add_subplot(111)

axes.plot(res1,'r-',label='10%')

axes.plot(res2,'g*',label='{:.1%}'.format(fk))

axes.plot(res3,'b-',label='50%')

axes.plot(res4,'k-',label='100%')

plt.legend(loc = 0)

plt.show()

效果图

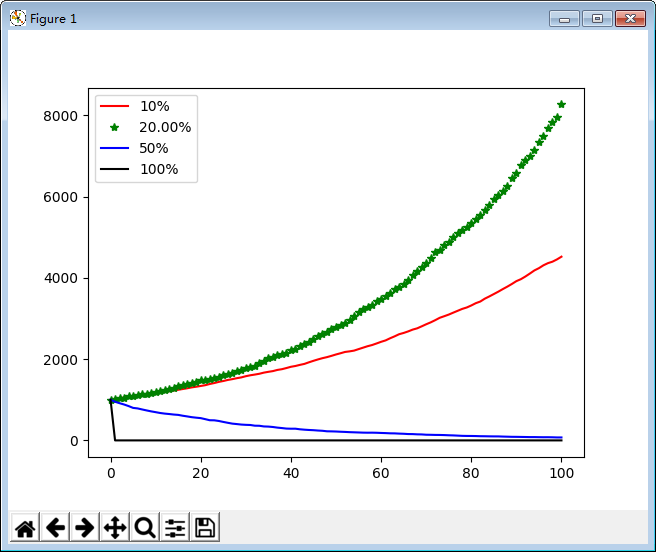
结论

由图显见，凯利值是最优的。